极大外平面图的Wiener 指标的上下界∗

孙晓慧，安新慧

(新疆大学数学与系统科学学院，新疆 乌鲁木齐 830017)

0 引言

1947 年,Wiener[1]首次引入连通图G 的Wiener 指标用于研究化学中石蜡的沸点.它是图G 的所有无序顶点对之间距离的总和.如果图G 是连通图且u,v ∈v(G),则u 和v 之间的距离d(u,v) 是连接u 和v 的最短路径上的边数.连通图G 的Wiener 指标W(G) 定义如下:

Entringer 等[2]证明了n 个顶点的树的Wiener 指标在其为星图时达到最小值(n-1)2,在其为路时达到最大值(n3-n)/6.Marraki 和Modabish 证明了n 个顶点的平面图的Wiener 指标的最小值为(n-2)2+2[3].Che和Collins 证明了当图G 是一个顶点数为n ≥3 的Apollonian 网络时,Wiener 指标的最大值为⎿(n3+3n2)/18」,并且进一步讨论了当图G 是顶点数为3 ≤n ≤10 的极大平面图的Wiener 指标的上界,并猜测它对所有n ≥3都成立[4].Ghosh 等证明了上述猜想,并确定了n ≥10 的极大平面图的Wiener 指标为Apollonian 网络时达到最大值[5].本文中我们主要研究了极大外平面图的Wiener 指标的上下界.

1 预备知识

本文仅考虑有限简单连通图,未指定的符号定义参阅文献[6].用N(v) 表示顶点v 的邻点集,基数|N(v)|是点v 的度数,记为d(v).集合S 的基数用|S| 表示.图G 的顶点集用V(G) 表示,其基数称为图G 的阶数.如果图G 中的任意两个顶点可通过路径连接，则称其为连通图.对于点x,y ∈V(G),d(x,y) 表示图G 中连接x和y 的最短路的长度.N(x,i) 表示图G 中与顶点x 的距离为i 的所有点的集合.特别的,当i=1 时,N(x,1)是x 的邻点集并且其基数等于x 的度数.图G 中顶点x 的离心率表示x 与图G 中其它顶点之间的最大距离,记为e(x).图G 的直径是所有顶点离心率的最大值,用diam(G) 表示.

定义1用W(x,G) 表示顶点x 和图G 中其它顶点之间所有距离的总和,即

图G 的Wiener 指标W(G) 表示G 中的无序顶点对之间的所有距离之和.图G 的Wiener 指标还可以表示为:

定义2外平面图是具有平面嵌入的平面图,其中每个顶点位于外部区域的边界上.若通过添加边获得的图不是外平面图,则此时的外平面图是极大外平面图.

对于给定的图G,我们使用G-x 表示通过删除顶点x 得到的图形.两个图G1和G2的连接,用G1∨G2表示,即将图G1中的每个顶点与图G2中每个顶点连接.我们首先给出极大外平面图的一些简单性质.

引理1设图G 是n 个顶点的极大外平面图(n ≥3),则

(i) 图G 中至少有两个2 度顶点.

(ii) 如果d(v)=2,那么图G-v 也是极大外平面图.

(iii) 图G 恰好有2n-3 条边.

定义3设P2n是通过将路Pn中所有距离为2 的顶点对之间连边后得到的图.

引理2[7]设图G 是n 个顶点的极大外平面图,其中n ≥5.若v 为图G 中1 个度为2 的点,并且其邻点为u 和w,则d(u)+d(w)≥7,等号成立当且仅当G[N(u)∪N(w)]∼=P25.

当n ≥3 时,令Hn表示n 个顶点的所有非同构的极大外平面图的集合.当n ∈{3,4,5},Hn包含唯一确定的图C3,H1,H2,如图1 所示.

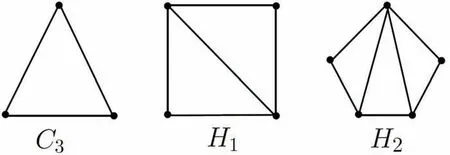
图1 C3,H1=P24,H2=P25

当n=6 时,H6={H′1,H′2,H′3} (如图2 所示).通过直接计算,可以得到

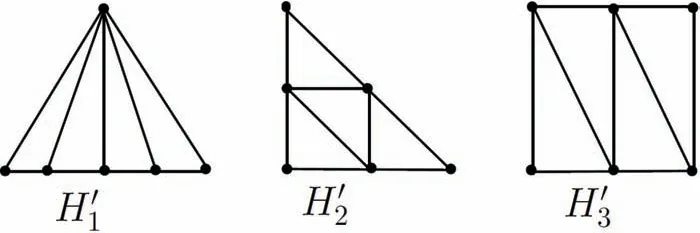
图2 H′1=K1 ∨P5,H′2,H′3=P26

W(H′1)=21,W(H′2)=21,W(H′3)=22.

在本文中,我们给出了极大外平面图的Wiener 指标的上下界,并刻画了相应的极图.

2 极大外平面图的Wiener 指标的下界

在本节中,我们将确定极大外平面图的Wiener 指标的下界,并刻画相应的极图.

引理3阶数n ≥7 的极大外平面图G 的直径为2 当且仅当G ∼=K1∨Pn-1.

证明显然,K1∨Pn-1是一个极大外平面图,并且直径为2.下面假设图G 是直径为2 且n ≥7 的极大外平面图.由引理1 可知,在图G 中存在v0∈V(G),它的度数d(v0)=2.设N(v0)={u0,w0}.由于图G 的直径是2,对于任何y ∈V(G){v0,u0,w0},有d(v0,y)=2.如果d(u0)=n-1 或d(w0)=n-1,则G ∼=K1∨Pn-1.下面考虑如果d(u0)

定理1设图G 为顶点数n ≥7 的极大外平面图,则W(G)≥n2-3n+3,等式成立当且仅当G ∼=K1∨Pn-1.

证明当图G 为极大外平面图且v ∈V(G),有

因此,可得

等式(1) 和等式(2) 成立当且仅当对任意u,v ∈V(G),有d(u,v)≤2.由于n ≥7,根据引理3,等式成立当且仅当G ∼=K1∨Pn-1.

3 极大外平面图的Wiener 指标的上界

在本节中,我们将确定极大外平面图的Wiener 指标的上界,并刻画相应的极图.

图3 为n 分别是偶数和奇数时的P2n的结构.

图3 P22k 和P22k-1

引理4[8]设Pn为顶点数n ≥3 的路,则

引理5[9]每个阶数至少为3 的极大外平面图都是2 连通的.

引理6设图G 为n 个顶点的2 连通图,则diam(G)≤⎿n/2」.

证明设x 是图G 中的顶点,e(x)=t,其中t>1.

注意,N(x,i) 对于0 ≤i ≤t 是两两不相交的,并且形成了图G 的顶点集的一个划分,从而

显然|N(x,0)|=1.当1 ≤i ≤t-1 时,N(x,i)是图G 的一个顶点割.由于图G 是2 连通的,对于1 ≤i ≤t-1有|N(x,i)|≥2.因此,n ≥2(t-1)+2=2t.那么e(x)=t ≤⎿n/2」,所以

引理7设图G 是n 个顶点的2 连通图.如果v ∈V(G) 且d(v)=2,那么

证明对n 个顶点的2 连通图G,有

因为|N(v,i)|≥2 (1 ≤i ≤t-1),

由于-t2+tn 在t 接近n/2 的整数处最大化,则

引理7 得证.

定理2设图G 为顶点数n ≥2 的极大外平面图,则

等式成立当且仅当G ∼=P2n.

证明设图G 是n 个顶点的极大外平面图.当n ≤5 时,显然图G 存在唯一的极大外平面图同构于P2n.

当n=6 时,由图2 可知,只有三个不同构的极大外平面图H′1,H′2,H′3.通过简单计算可得,W(H′1)=21,W(H′2)=21,W(H′3)=22.由于H′3∼=P26,所以n=6 时,结果成立.

当n ≥7 时,我们对顶点数n 使用数学归纳法证明,若G ≇P2n,则W(G)

情况1 图G 至少有三个2 度顶点.

图G 存在两个2 度顶点,记为u 和v,使得d(u,v)<⎿(n-1)/2」-1.这意味着当w 是与u,v 不同的2 度顶点时,G-w ≇.设G′=G-w.

情况2 图G 恰好有两个2 度顶点.

图G 的两个2 度顶点记为u 和v,由于G ≇P2n,因此至少存在一个顶点w,其度数至少为5.因此,图G-u和G-v 中的至少有一个与Pn2-1不同构.不失一般性,假设G-u ≇,因此设G′∼=G-u.

由于图G′是一个顶点数为n-1 的极大外平面图,且G′≇,根据归纳假设,W(G′)

由于

将式(3) 代入式(4) ,利用引理7,我们得到

定理得证.