基于浸入与不变原理的分数阶HR神经元同步控制∗

王琦，王聪，马萍，张绍华

(新疆大学电气工程学院，新疆 乌鲁木齐 830017)

0 引言

神经元是神经系统的基本单位，也是神经系统的核心模块．近年来，由于神经元在脑脉冲、模式识别和脑信号测量等方面有着重要的理论和应用价值，已成为神经科学研究的热点[1]．神经元传输编码信息的能力依赖于它们与相邻神经元的同步能力，实验证明神经元的同步能力与认知功能有关，目前发现同步是神经信息处理和神经疾病（癫痫[2]和帕金森病[3]等）治疗的最佳机制，因此探究神经元的同步行为对神经科学具有重要意义．

随着神经科学的不断发展，人们相继提出各种神经元模型，如Hodgkin-Huxley（HH）[4]、FitzHugh-Nagumo（FHN）[5]和Hindmarsh-Rose（HR）[6]等．在各种神经元模型中，HR神经元模型不仅具有简单的多项式形式，方便计算，而且能够准确地表现出大多数放电行为，如静止态、峰值放电、簇发放电等．这些特点使得HR神经元模型成为放电分析和同步控制最常用的模型．

分数阶微分方程近年来被认为是理想的整数阶微分方程的推广，可以更有效地预测和评估神经元放电频率，并且可以更加准确地描述一些物理现象．Dong等[7]用分数阶导数研究了HR神经元模型的动力学行为，结果表明：随着分数阶的改变，神经元表现出不同的放电模式（混沌和周期放电），并且分数阶模型的放电频率高于整数阶模型．因此，本文选择分数阶HR神经元模型作为研究对象．

近年来，通过李雅普诺夫理论分析，在神经元同步控制中应用了许多先进的控制理论和控制方法，如自适应控制[8-10]、滑模控制[11-12]等．Semenov等[13]基于有界性分析和速度梯度法，研究了异构HR神经元的自适应同步问题；Cimen等[14]实现了两个磁流效应下HR神经元同步的最优控制方法．Liu等[15]利用李雅普诺夫方法推导了分数阶扩展HR神经元模型的神经网络滑模算法，实现了在磁声刺激输入下的广义投影同步问题；Tene等[16]通过Ge-Yao-Chen偏区域稳定理论实现了分数阶神经元的同步问题，并发现分数阶导数相比整数阶导数具有更快的同步速度．但是以上研究大多没有考虑系统内部不确定性对同步控制的影响，且大多自适应方法在系统参数估计上具有一定局限性．

针对以上研究不足，本文提出了一种基于浸入与不变原理的自适应分段滑模同步方案．浸入与不变原理是通过建立不变流形，基于保持流形的吸引性与不变性来实现对扰动误差的估计，在航天器、无人机等复杂非线性系统中均取得了很好的效果[17-18]，但是在神经元同步领域尚未应用．因此，本文使用这一思想对神经元系统的内部不确定性和外部扰动进行自适应估计，相比传统自适应方案，提高了扰动估计的灵活性，也改善了系统的控制性能．同时，结合传统滑模趋近律和饱和函数，提出一种新型的分段滑模趋近律，提高同步速度并有效降低滑模抖振．通过Lyapunov稳定性分析和仿真验证，本文所提控制方案实现了驱动-响应分数阶HR神经元系统的完全同步，为神经元的同步控制和通讯安全等研究提供了一定的参考．

1 预备知识和模型描述

1.1 预备知识

采用Caputo分数阶导数来对模型进行描述，接下来介绍以下预备知识：

定义1Caputo分数阶导数定义如下：

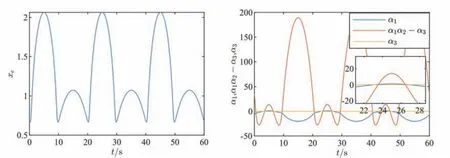
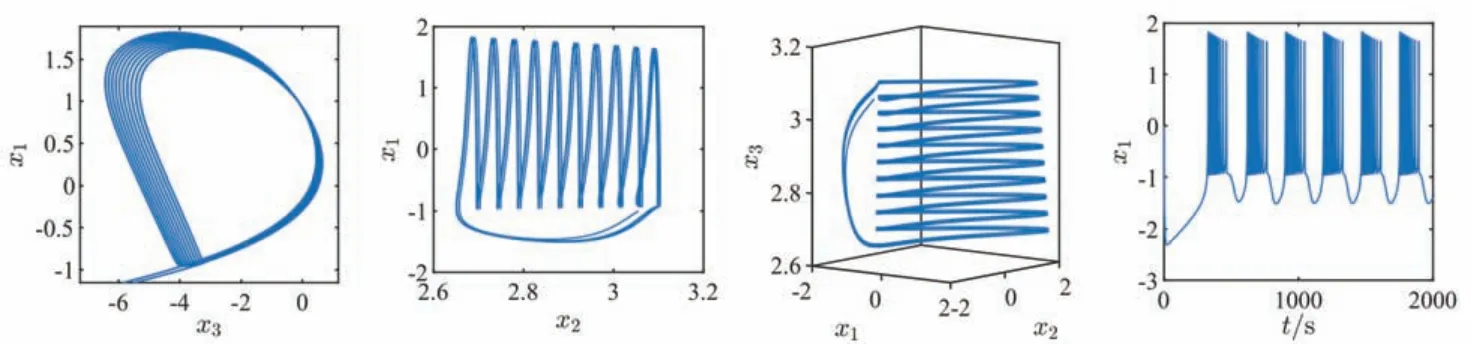
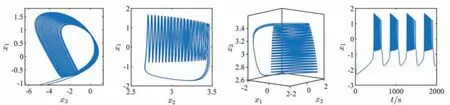
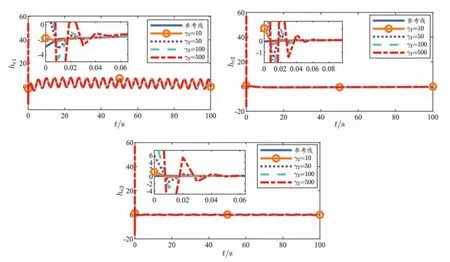
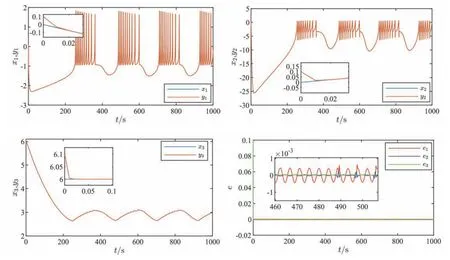
其中：t ≥0，q为分数阶阶数，n是满足n-1

定义2Riemann-Liouville分数阶积分定义如下：

其中：t ≥0，q为分数阶阶数，Γ(·)是Gamma函数，Iqt为分数阶积分算子．

以下分数阶微积分性质将在后文中用到：

性质1若q1>0,q2>0，并且q1+q2<1，那么：

并且Dt1-q(Dtqx(t))=Dx(t)=x(t)，0

性质2若n-z

性质3若0

1.2 分数阶HR神经元数学模型

当细胞内的离子（如钙、钾、钠离子）的浓度发生变化时，就会引起膜电位的波动．因此，施加超过阈值的外部电流刺激，可以诱导神经元的动作电位发生变化．三维的HR神经元模型由三个一阶常微分方程表示：

其中：x1表示细胞的膜电位，x2表示恢复性的快速离子交换电流（钠离子和钾离子的交换，也称尖峰变量），x3表示其它离子的适应性慢离子交换电流，也称爆发变量．a、b、c、d均为系统的模型参数．Iext表示外部输入电流，参数r为慢速离子交换通道的离子交换速度控制变量，s为可调适应参数，x0表示静息膜电位．

分数阶微分模型作为整数阶微分模型的扩展，不但涵盖了整数阶模型的全部特性，并且可以更加详细地刻画出实际系统的记忆和遗传特性，所以分数阶模型在展现神经元动力学行为方面更有优势，因此基于Caputo分数阶导数建立的分数阶HR神经元模型如下：

其中：Dqt是Caputo分数阶导数算子．状态变量和模型参数与整数阶HR神经元模型具有相同的物理意义．接下来对模型的平衡点进行分析，令式（7）左边为0可得：

由式（8）可得，模型的平衡点为：

xe可以由以下一元三次方程的实根确定：

其中：A=(d-b)/a，B=s/a，C=-(sx0+c+Iext)/a．定义xe=ye-(d-b)/3a，式（10）可以改写为：

其中：p=B-A2/3、q=C+2A3/27-AB/3，判别式∆=q2/4+p3/27．考虑给定如下系统参数：a=1、b=3、c=1、d=5、r=0.002 1、s=4、x0=-1.6，此时平衡点E=(xe,1-5x2e,4xe+6.4)，p=8/3、q=89.8/27-Iext．显然，对于任意Iext均满足∆>0，此时式（11）有一个实数根和两个复数根，由于平衡点不能是复数，所以在此系统参数下模型只有一个平衡点，其中ye为：

在平衡点E处，模型（7）的雅可比矩阵为：

可得特征方程为：

其中：α1=3x2e-6xe+1.002 1，α2=3.006 3x2e+3.987 4xe+0.010 5，α3=0.006 3x2e+0.008 4xe+0.008 4．

可通过Routh-Hurwitz判据来对平衡点进行稳定性判断，当劳斯判据参数α1>0、α3>0、α1α2-α3>0时，平衡点是稳定的．当外部输入电流Iext为直流电流时，例取Iext=3，此时平衡点可求得E=(-0.788 2,-2.106 4,-3.247 1)，三个特征值为λ1=0.158 5、λ2=0.004 6、λ3=-7.758 2，表明此时平衡点为不稳定平衡点；当外部输入电流Iext为交流电流时，例取Iext=20sin(0.1πt)，模型的平衡点和劳斯判据参数变化曲线如图1所示，在由Iext引起的整个周期的时间区间[15,35]中，交流平衡点E只有一个稳定区间[23.533,26.469]，其余交流平衡点均不稳定．

图1 平衡点和劳斯判据参数曲线

接下来对引入分数阶导数的意义进行分析，取Iext=3，初始向量选定为x(0)=[0,0,6]T，整数阶和分数阶取0.95、0.93时的系统相图和时序图如图2、图3、图4所示．由图2可知，整数阶神经元的放电模式呈现十峰周期的簇发放电状态；由图3可知，当分数阶阶数取0.95、且其它参数不变时，神经元的放电模式变为十七峰周期的簇发放电状态，因此引入分数阶导数可以加剧神经元的放电频率，且分数阶阶数越低，放电行为越剧烈．由图4可知，当分数阶阶数取0.93时，神经元的放电模式呈现半圆形的簇发放电状态，因此引入分数阶导数还可以使得HR神经元呈现出更加丰富的放电状态．

图2 整数阶系统相图和时序图

图3 分数阶阶数取0.95时系统相图和时序图

图4 分数阶阶数取0.93时系统相图和时序图

分数阶HR神经元模型不可避免的会受到外界刺激的影响，使得神经元的放电状态发生各种变化．因此，在考虑外部输入交流电流Iext=Imsin(2πFt)的影响下，对模型进行分岔分析．式中：Im、F分别为交流电流幅值和频率，当F=0.225、分数阶阶数取0.95时，调整Im从3变化到8的分岔图如图5所示．可知随着Im的逐渐增加，神经元模型呈现出各种复杂的动力学行为，如周期、倍周期、混沌放电等．

图5 Im从3变化到8时模型分岔图

2 控制器设计

考虑基于浸入与不变原理的两个以驱动-响应结构相互连接的分数阶HR神经元模型的滑模同步问题．驱动神经元模型如下：

受控的响应神经元模型如下：

其中：dri(i=1,2,3)为未知的外部扰动，ui(i=1,2,3)为响应神经元各状态变量的控制输入．驱动-响应HR神经元系统具有未知的非线性项参数a1、a2、b1、b2、d1和d2，以及未知的常数项x0和y0．

为了评价控制器的同步性能，同步误差可以定义为ei=yi-xi,i=1,2,3，所以驱动-响应HR神经元的误差系统可以定义为：

其中：y=[y1,y2,y3]T、x=[x1,x2,x3]T分别表示驱动和响应神经元的状态变量．可知误差向量的分数阶导数为：

为了简化推导过程，并将系统内部不确定性和外部扰动作为系统的总扰动，误差系统可以写成如下形式：

参数矩阵的定义如下：

其中：A是常数矩阵，he=[he1,he2,he3]T为系统的总扰动，包含系统未知非线性项、未知参数项和未知外部扰动项，u表示作用于响应分数阶HR神经元的控制输入向量．为了便于设计，令g=[g1,g2,g3]T=Ae．控制器的设计目的是存在系统内部不确定性和外部扰动的情况下，驱动状态向量y跟踪状态向量x的时变轨迹．

2.1 自适应分段滑模控制器设计

接下来进行滑模控制器设计，滑模面向量定义为s=[s1,s2,s3]T，为了简化控制器设计和稳定性分析，设计分数阶积分滑模面如下：

其中：i=1,2,3，k1为正常数．对式（20）求分数阶导数可得滑模面的分数阶导数为：

当系统运动在滑模面上时，需要满足si==0，且由Dqtsi=0可得，=D1-qtDqtsi=0，因此只需要满足s=Dqtsi=0即可．从而可以得到Dqtei=-k1ei，易得此时ei是稳定的且可以收敛到0．

为了提高系统的响应速度并且消除滑模抖振，结合常用的指数趋近律Dqts=-k1sgn(s)-k2s、饱和函数和正切函数，设计了一种新的滑模趋近律：

其中：c1>0、c2>0、µ1>0、µ2>0、σ>0、0<ϕ<1，可以通过调整µ1、µ2和σ的取值，灵活调整当系统位于滑模面外的趋近速度．

当|s|>ϕ时，误差系统远离滑模面，此时的滑模趋近律为Dqts=-c1exp(|s/µ1|)sgn(s)-c2sexp(|s/µ2|)．易得c1exp(|s/µ1|)>c1、c2exp(|s/µ2|)>c2，因此所提出的滑模趋近律相对常用的指数趋近律收敛速度更快，且在误差系统靠近滑模面的过程中，c1exp(|s/µ1|)和c2exp(|s/µ2|)也在逐渐减小，可以起到降低滑模抖振的效果．

当|s|≤ϕ时，误差系统靠近滑模面，此时的滑模趋近律为Dqts=-c1exp(|s/µ1|)tanh(s/σ)-c2sexp(|s/µ2|)．当|s|→0时，Dqts=-c1exp(|s/µ1|)tanh(s/σ)-c2sexp(|s/µ2|)→0，但Dqts=-k1sgn(s)-k2s →k1，故所提出的滑模趋近律相对常用的指数趋近律可以更好地消除滑模抖振，且更灵活、可以更快地达到收敛效果．

接下来将所提滑模趋近律应用于本文系统中，将式（19）代入式（21）可得：

控制器如下所示：

定理1针对所提驱动-响应分数阶HR神经元系统，使用所提新的滑模趋近律可以使误差系统收敛到0．

证明考虑Lyapunov函数v1=式中：=hei-为hei的估计误差，γ1>0．对v1求分数阶导数，将式（24）和式（25）代入并结合性质3得：

当|si|>ϕ时．

当|si|≤ϕ时．

由以上分析可知，控制器稳定，定理1得证．

相比传统使用Lyapunov稳定性理论设计的自适应率，利用浸入与不变原理设计的自适应律中引入了额外的补偿函数，从而使对总扰动的估计由积分转换为比例积分，加强了对总扰动自适应律设计的灵活性，进而改善了自适应非线性系统的控制性能，因此本文接下来应用浸入与不变原理推导出新型自适应律来对误差系统总扰动进行估计．

2.2 基于浸入与不变原理的自适应分段滑模控制器设计

基于浸入与不变原理，对误差系统的总不确定性估计建立如下不变流形：

其中βi(ei)是一个待定的连续函数，以满足所定义的流形（29）不变，可将误差系统的动力学方程（19）扩展为：

其中ψi(i=1,2,3)是总扰动估计值的自适应律．由于未知的总扰动hei被排除在Dqtei的表达式之外，若Dqtei和偏离流形M，那么式（30）就不再成立，因此需要设计一个变量来使流形M具有吸引力和不变性，考虑流形外变量zi(i=1,2,3)有如下定义：

通过使用zi，误差系统可以改写为：

对zi求分数阶导数且将式（30）和式（32）代入可得：

通过分析式（33），取自适应律ψi为：

由式（33）和式（34）可得：

通过分析式（35），可以取：

其中γ2>0．则有Dqtzi=-γ2zi，易知此时zi可以收敛到0．

对式（36）两边取分数阶积分可得：

由式（37）结合性质2可得：

再由式（2）和式（37）可得：

结合式（38）和式（39）可得：

化简式（40），取βi(0)=0可得：

定理2使用设计的式（34）自适应律和式（41）补偿函数，可以使定义的zi稳定且可以收敛到0，并使流形M保持不变、具有吸引力．

证明考虑Lyapunov函数v2=z2i/2，求分数阶导数且代入式（35）可得：

即zi可以收敛到0，定理2得证．

结合本节方法和式（20∼23）所提滑模面和滑模趋近律，考虑控制器设计如下：

由式（21）、式（32）和式（43）可得：

定理3针对所提驱动-响应分数阶HR神经元系统，使用所提基于浸入与不变原理的自适应滑模控制器可以使误差系统收敛到0．

证明考虑Lyapunov函数v3=s2i/2+z2i/(2γ2)，求分数阶导数，结合上述分析且将式（44）代入可得：

当|si|>ϕ时．

当|si|≤ϕ时．

若取c1>0、c2>1/4，即可实现Dqtv3≤0，从而定理3得证．

通过上述推导，基于浸入与不变原理的自适应分段滑模控制器设计完毕，应用所提方案，可以使驱动-响应分数阶HR神经元系统达到同步．

3 仿真验证

驱动-响应分数阶HR神经元模型的具体参数为a1=1、a2=1.2、b1=3、b2=3.6、c=1、d1=5、d2=5.3、r=0.002 1、s=4、x0=-1.6、y0=-1.8，系统的初始向量选取为x(0)=[0,0,6]T、y(0)=[0.1,0.1,6.1]T，分数阶阶次取0.95．外部输入交流电流分别为Iext1=3和Iext2=4sin(0.45πt)．响应系统的外部扰动选取为dr1=sgn(t)、dr2=tanh(t)和dr3=0.2cos(t)．接下来对控制器的参数分析和控制效果进行仿真验证．

3.1 参数分析

由于本文所提基于浸入与不变原理的自适应分段滑模控制器的不同控制参数会对驱动-响应分数阶HR神经元系统的状态变量同步以及扰动跟踪的效果产生较大影响，所以对不同控制器参数变化进行了对比实验．当控制器参数变化时系统总扰动跟踪曲线如图6所示，其余控制器参数选取为k1=50、c1=50、c2=6、µ1=µ2=0.6、ϕ=0.2、σ=0.5．由图6可知，虽然γ2取不同值时均可使控制器在有限时间内实现对总扰动的跟踪，但是随着γ2的不断增大，控制器对总扰动跟踪的超调量会明显增大，且收敛时间也会相应增加．

图6 γ2变化时系统总扰动跟踪曲线

控制器参数k1的选取对驱动-响应分数阶HR神经元系统的同步曲线影响如图7所示，其余控制器参数选取为c1=50、c2=6、µ1=µ2=0.6、ϕ=0.2、σ=0.5、γ2=10．由图7可知，若k1的值过小会使同步的稳态误差增大．随着k1的增大，控制器的同步速度会加快，但是过大的k1值会使同步曲线出现超调，影响同步速度．

图7 k1变化时系统同步曲线

由以上分析可知，本文所提控制器的参数应该合理选取，其它控制器参数的选取也是由大量实验所得，在此不再赘述．控制器参数选取确定为k1=50、c1=50、c2=6、µ1=µ2=0.6、ϕ=0.2、σ=0.5、γ2=10．

3.2 控制器同步效果与方法对比

选取以上参数，本文所提控制器的同步效果如图8所示．在控制器的作用下，响应分数阶HR神经元的状态变量立即跟随驱动分数阶HR神经元的状态变量，并具有相同的状态轨迹，误差也收敛到一个相当小的区间内，实现了完全同步．由此可见，本文所提方案是具有鲁棒性的，即使存在内部不确定性和外部扰动的前提下，也可以实现驱动-响应分数阶HR神经元的完全同步．

图8 系统同步效果和误差曲线

为了验证所提方案的优越性，将其与方法1（自适应滑模控制器）和方法2（基于非线性扰动观测器的自适应滑模控制器）进行对比实验．图9是驱动-响应分数阶HR神经元系统的状态变量在3种控制器作用下的同步曲线．相比其它两种控制方式，所提基于浸入与不变原理的自适应分段滑模控制器同步时间更短，超调量更小，过渡过程更平滑，稳态误差也更小．

图9 不同控制器状态变量同步曲线

通过对比进一步说明，引入浸入与不变原理后，系统状态变量的同步速度和对系统内部不确定性的适应能力相比其它两种控制方法都得到了一定的提升，并且可以有效降低稳态误差和抖振现象，体现出本文所提方案的优越性．

4 结论

以分数阶HR神经元为研究对象，针对驱动-响应分数阶HR神经元完全同步问题提出了基于浸入与不变原理的分段滑模同步方案，并与其它两种控制器进行对比实验，结果表明：在保证控制器可以使神经元系统达到稳定同步的前提下，相比自适应滑模控制器和基于非线性扰动观测器的自适应滑模控制器，本文所提控制器提高了传统方法对扰动的跟踪性能，并降低了控制器抖振，证明所提方案的可行性与优越性．