有向圈码

赵 颖,王 燕

(烟台大学数学与信息科学学院,山东 烟台 264005)

1 引言与预备知识

本文中,关于有向图的基本定义和术语可以参考文献[1]。设Γ是有点集V(Γ)和弧集A(Γ)的一个连通的有向图。一条弧(u,v)的两个端点u和v分别称为这条弧的尾部和头部。假定∅≠S⊆V(Γ),如果对于任意的u,v∈S,(u,v)∉A(Γ)并且(v,u)∉A(Γ),则称子集S为一个孤立点集。

定义1 假定S是有向图Γ的一个孤立点集。如果对于每一个v∈V(Γ)S,存在唯一的元素x∈S使得(v,x)∈A(Γ),则S称为Γ的一个完备核,而如果对于每一个w∈V(Γ)S,存在唯一的元素y∈S使得(y,w)∈A(Γ),则称S为Γ的一个完备解。而Γ的一个完备有向码(也称为有效双向控制集)是V(Γ)的一个孤立点集S,它既是一个完备核也是一个完备解。

对于一个无向图,不需要区分完备核和完备解而统称为完备码(也称为有效控制集或独立完备控制集)。完备码的研究结果比较多[2-7],但是到目前为止,有向图的完备有向码的研究结果不如无向图的完备码的研究结果丰富。文献[8-18]对于de Bruijn 和Kautz digraph等图类中有向完备码做了相关研究。

定义2 设G是一个群,X={x1,x2,…,xn}是G的一个子集。凯莱有向图Γ=Cay(G,X)的点集为G,任取g,h∈G,(g,h)∈A(Γ)当且仅当存在x∈X使得h=xg。

由定义2可知,如果X=X-1,则它是一个凯莱图(无向)。如果为了避免自环,则X中不含群的单位元。容易验证,有向图Cay(G,X)是连通的当且仅当X生成G。

例1 在8阶循环群G=〈a〉中,取X0={a,a2,a3},则{1,a4},{a,a5},{a2,a6},{a3,a7}同时是Cay(G,X)的完备核与完备解,见图1。

图1 Cay(G,X0)中的完备核和完备解

例2 在6阶二面体群D6=〈ρ,τ|ρ3=τ2=1,τ-1ρτ=ρ-1〉中,取X={ρ,τ},则{τ,ρ2}是凯莱有向图Cay(D6,X)的一个完备核但不是完备解。同样,{1,τρ2}是凯莱有向图的一个完备解但不是完备核,见图2。

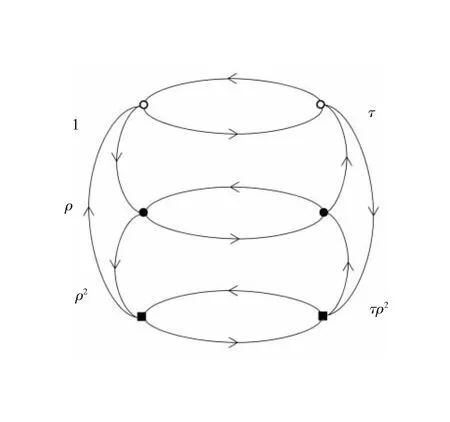
图2 Cay(D6,X)中的完备核{τ,ρ2}和完备解{1,τρ2}

定义3Cay(G,X)的一个自同构指的是作用在G上的一个既单且满的映射σ使得(u,v)是一条弧当且仅当(σ(u),σ(v))是一条弧。

选取G中的一个元素g,定义Rg:G→G满足:对于每个元素u∈G有Rg(u)=ug。容易看出Rg是G上的一个既单且满的映射,并且(u,xu)(x∈X)是一条弧当且仅当(ug,xug)是一条弧,因此Rg是Cay(G,X)的一个自同构。

定义4在一个有向图Γ中,假定存在V(Γ)的两个子集S1,S2满足S1∩S2=∅,|S1|=|S2|且任取v∈S2存在唯一的u1∈S1和唯一的u2∈S1(u1和u2可以是同一个点)使得(u1,v)∈A(Γ), (v,u2)∈A(Γ)。反之任取u∈S1,存在唯一的v1∈S2和唯一的v2∈S2(v1和v2可以是同一个点)使得(v1,u)∈A(Γ),(u,v2)∈A(Γ),则称S1与S2之间存在一个有向匹配。容易验证,两个集合之间的有向匹配是若干个相互独立的有向圈的并集。

例3 令S1={u1,u2,u3},S2={v1,v2,v3},则S1和S2之间有两种有向匹配,见图3。

图3 S1与S2之间的两种有向匹配

有向完备码是孤立点集可以控制有向图的所有顶点,本文考虑一个有向圈可以控制有向图中所有顶点的情况,即题目中的有向圈码。

定义5在一个有向图Γ中,如果存在一个有向圈C,满足对于任意的u∈V(Γ),C上存在唯一的一个顶点c1和唯一的一个顶点c2(c1和c2可以相同)使得(c1,u)∈A(Γ),(u,c2)∈A(Γ),则称C是Γ的一个有向控制圈,称长度最小的有向控制圈为有向圈码。

本文中,如果在一个有向圈C上从某个顶点开始,不妨设为u1,沿着圈的方向经过的顶点依次为u2,…,um,u1,则将C记作C=(u1,u2,…,um)。比如,图2中长度为3的有向圈(1,ρ,ρ2)为Cay(D6,X)的一个有向圈码。

2 有向圈码

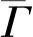
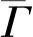
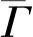
证明只需证明:任取u∈V(Γ),C上存在唯一的一个点c1使得(u,c1)∈A(Γ)和唯一的一个点c2使得(c2,u)∈A(Γ)。

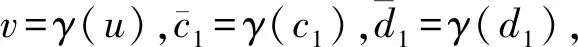
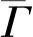
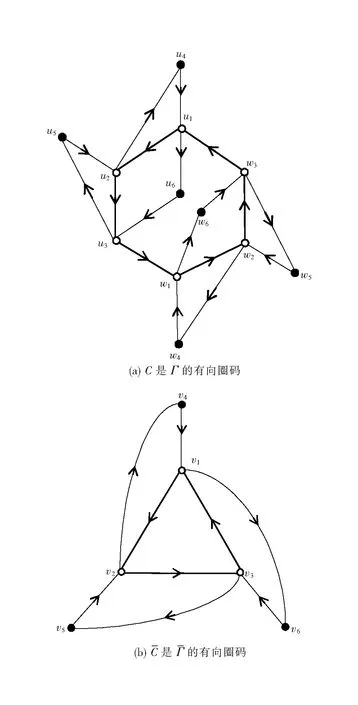
图4 Γ是的2重覆盖,C覆盖

定理2 (1)有向图的有向圈码的圈长相同。

(2)假定C1,C2是有向图Γ的两个没有公共顶点的有向圈码,则Γ(V(C1)∪V(C2))是Γ的一个有向匹配。

证明根据有向圈码的定义易得结论(1)。

(2) 设C1=(u1,u2,…,um)和C2=(v1,v2,…,vm)是有向图Γ的两个无公共顶点的有向圈码。由于C1是一个有向圈码,任取vi,1≤i≤m,在C1中存在唯一的一个顶点us和唯一的一个顶点ut,1≤s,t≤m使得(us,vi)∈A(Γ),(vi,ut)∈A(Γ),这里s和t可以相等。同理,由于C2也是一个有向圈码,任取uj,1≤j≤m,在C2中存在唯一的一个顶点vk和唯一的一个顶点vl,1≤k,l≤m使得(vk,uj)∈A(Γ),(uj,vl)∈A(Γ),这里k和l可以相等。这就说明,Γ(V(C1)∪V(C2))是一个有向匹配。

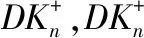
图5 Γ覆盖

图6 Γ是的4重覆盖

3 凯莱图的有向圈码

在本文中,如果一个有向图的每个顶点的出度和入度都分别对应相等, 我们称这个有向图为一个正则有向图。

引理1 假定Γ是一个正则有向图,每个点的出度为s,入度为t。如果C是Γ的一个有向圈码, 则s=t且|V(Γ)|=|V(C)|s。

证明根据有向圈码的定义可知:

|V(Γ)|=|V(C)|s=|V(C)|t,

因此s=t且|V(Γ)|=|V(C)|s。

凯莱有向图Cay(G,X)是一类典型的正则有向图,且其顶点的出度和入度相等,都等于|X|。

定理3假定Γ=Cay(G,X)是有限群G相应于X={x1,x2,…,xn}的一个凯莱有向图,C=(c1,c2,…,cm)是Γ的一个有向圈。则C是Γ的一个有向圈码当且仅当以下任意一条成立:

(1)对任意的g∈G,Cg=(c1g,c2g,…,cmg)是Γ的一个有向圈码。

(2)集合G既可以划分成n个子集:

Si=(xic1,xic2,…,xicm),1≤i≤n,

也可以划分成n个子集:

证明(1)如果C是一个有向圈码,则对于Cay(G,X)的每个自同构φ,φ(C)也是一个有向圈码。对任意g∈G,Rg是Γ的一个自同构,所以Rg(C)=Cg是一个有向圈码。

反过来,Rg-1(Cg)=C在Cg是一个有向圈码的条件下是一个有向圈码。

(2)假设C是Γ的一个有向圈码,根据有向圈码的定义G可以划分成m个子集:

Vi={x1ci,x2ci,…,xnci},1≤i≤m,

也可以划分成m个子集:

将m个子集Vi,1≤i≤m重新组合,令

Si={xic1,xic2,…,xicm},1≤i≤n,

即可得到G的一个新划分。

同理,可以得到G的划分:

反过来,假设G可以划分成n个子集:

Si={xic1,xic2,…,xicm},1≤i≤n。

对于每个a∈G,存在唯一的一个子集,比如St,使得a∈St,即a=xtcj。这说明V(C)中存在唯一的cj使得(cj,a)∈A(Γ)。

同理,如果G可以划分成n个子集:

Ti={xi-1c1,xi-1c2,…,xi-1cm},1≤i≤n,

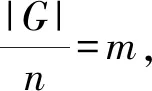
假定G是一个有限群,H是G的一个子群,集合{a1,a2,…,am}⊆G称为H在G中的一个左陪集代表系。如果其满足aiH∩ajH=∅(1≤i≠j≤m)且G=a1H∪a2H∪…∪amH。同理可以定义H在G中的一个右陪集代表系,由群论理论可知左陪集代表系和右陪集代表系中包含相同数目的元素。

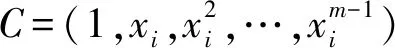
x1Hi,x2Hi,…,xnHi

和

反之,假定X既是Hi的一个左陪集代表系也是Hi的一个右陪集代表系。则首先Hi∩X={xi},其次

x1Hi,x2Hi,…,xnHi

和

例6G=〈a〉={1,a,a2,a3,a4,a5} 是一个6阶循环群,取X={a,a2,a3},子群H=〈a3〉。则X是H的一个左(右)陪集代表系,C=(1,a3)是Cay(G,X)的一个有向圈码,如图7所示。

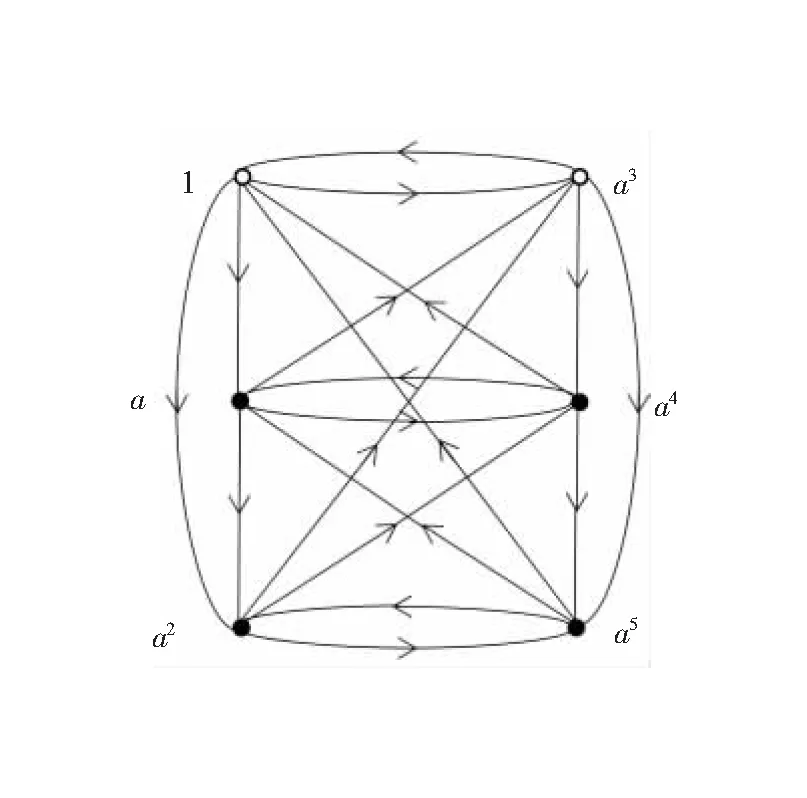
图7 有向圈码(1,a3)