核心素养导向下的问题驱动式教学——以“两角差的余弦公式”为例

⦿ 湖北大学数学与统计学学院 赵 薇 徐运阁

《普通高中数学课程标准(2017年版2020年修订)》提出高中数学的课程目标之一就是发展学生的核心素养,学者章建跃也提出“教好数学就是落实核心素养”.那么,六大核心素养怎样才能落地生根?什么样态的知识教学有利于学科核心素养的发展?学者李松林认为问题驱动的整合式教学有利于学生核心素养的发展,并提出学习即持续的自主建构,学生的学习及核心素养的发展最终依靠的都是学生本身的内源性学习力.因此,教师需要做的就是通过自己精心设计的教学来驱动学生的内源性学习力,无疑问题驱动式教学就是有效的教学模式之一.

1 教材分析

三角恒等变换是高一学生需要掌握的重点内容,两角差的余弦公式是“三角恒等变换”这一节的基础和出发点,也是前面所学三角函数知识的继续与发展.由于和与差内在的联系性与统一性,教材选择两角差的余弦公式作为基础,使公式的证明过程尽量简洁明了,易于学生理解和掌握.教材没有直接给出两角差的余弦公式,因此可以利用问题驱动学生结合本章已学的知识与方法进行自主探究,引导学生大胆猜想、小心求证,鼓励学生发散思维、创新方法.

2 教学目标

(1)掌握两角差的余弦公式,能正确运用公式进行简单的求值运算;

(2)经历用平面直角坐标系、单位圆、两点间的距离公式推导两角差的余弦公式的过程,进一步体会平面直角坐标系和单位圆对于三角函数的重要作用;

(3)在探究过程中,体会“转化与化归”“分类讨论”“数形结合”等数学思想方法,体会数学思维的合理性与条理性.

3 教学过程

3.1 课程引入,提出问题

问题1某城市电视发射塔建在市郊的一座小山上(如图1),沿着山坡有一条坡度为15°,长为200 m的小路可以从山底直达塔底,在小路最底端测得电视信号发射塔塔尖的仰角为60°,求塔尖到地面的距离.

图1 现实情境

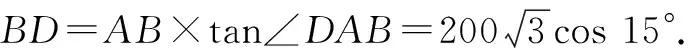
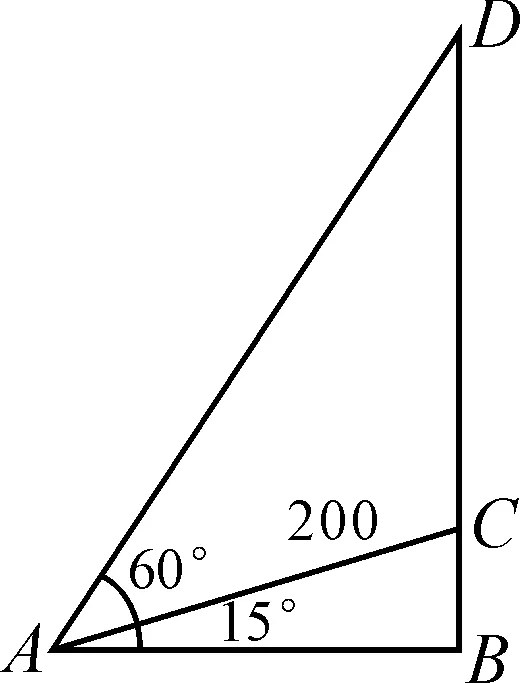
图2 数学模型

追问1:cos 15°=?

追问2:cos 15°=cos(60°-45°)=?

追问3:更一般地,对于任意角α,β,cos(α-β)=?

设计意图:从实际问题出发,有利于强调数学与实际的联系,使学生感受到研究差角公式的必要性,让学生经历将现实情境抽象成数学问题的过程,有利于培养数学抽象素养.强调用已知角表示未知角,让学生体会将未知转化为已知的转化与化归思想.

3.2 联系旧知,形成猜想

问题2同学们之前见过哪些两角差的余弦呢?

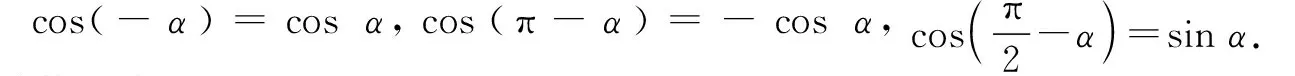
追问1:观察这6个式子的结果,有什么发现吗?

师生活动:学生回答,教师总结.这6个式子的结果涉及到cosβ,sinβ,cosα,sinα这4个三角函数值,于是猜想cos(α-β)与cosβ,sinβ,cosα,sinα有关!

追问2:cos(α-β),cosβ,sinβ,cosα,sinα的数学意义是什么?

师生活动:引导学生根据三角函数的定义回答.当角的始边与x轴的非负半轴重合时,cosα与sinα;cosβ与sinβ分别是角α,β的终边与单位圆交点的横、纵坐标;cos(α-β)是角α-β的终边与单位圆交点的横坐标.

设计意图:该环节体现了从特殊到一般的思想,联系以前学过的诱导公式,让学生经历探究发现的过程,而不是直接告诉学生结论.最后引导学生从最本质的定义出发说出各三角函数值的数学意义,也意在提示学生要注重对数学定义的理解和记忆.

3.3 探究发现,得出结论

利用平面直角坐标系、单位圆,结合两点之间的距离公式,推导两角差的余弦公式.

师生活动:学生动手操作,将上述数学符号在图中表示出来.有学生将角α,β的终边画在了一起(预设),此时α=β+2kπ(k∈Z),对应cos(α-β)=1.接着探究一般情况,假设α,β的终边不重合,也就是α≠β+2kπ(k∈Z),提示学生不必纠结角α,β终边的位置问题,因为cos(α-β)=cos(β-α),为了研究方便这里将角α的终边画在角β终边的上方,就可得到角α,β的终边与单位圆交点的坐标分别为P1(cosα,sinα),A1(cosβ,sinβ).

问题3角α-β的始边、终边分别是什么?

师生活动:有学生提出∠A1OP1就是α-β(预设).教师提示,根据角的减法,角α-β的始边就是角β的终边,角α-β的终边就是角α的终边,则α-β=∠A1OP1+2kπ(k∈Z),但此时∠A1OP1没有在标准位置上,也就是始边没有与x轴的非负半轴重合,无法得到cos(α-β),所以将角α-β的始边、终边一起旋转,使其始边与x轴的非负半轴重合,则角α-β的终边与单位圆交点P的坐标为(cos(α-β),sin(α-β)),令单位圆与x轴正半轴的交点为A(1,0).

问题4观察图3,并联系刚才得到的点的坐标,可以得到什么等量关系?

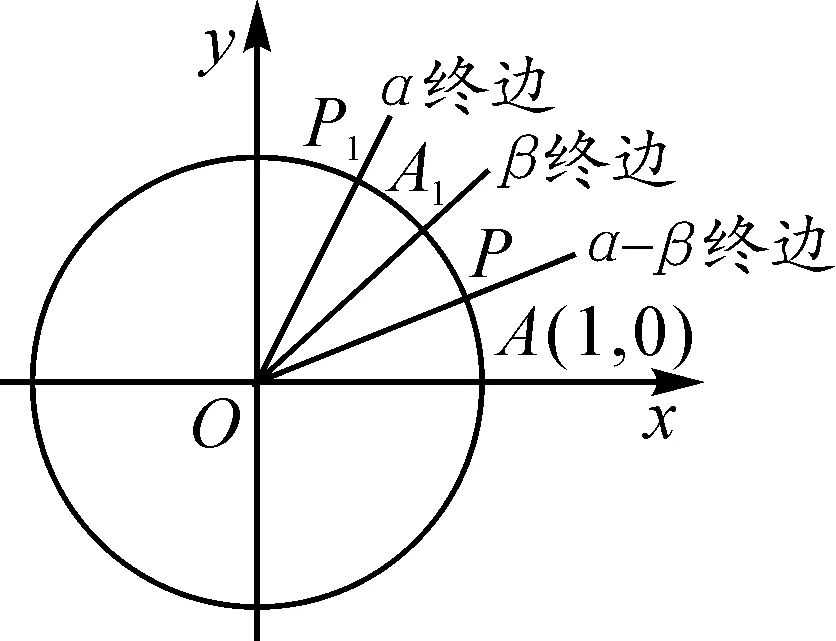
图3

追问:到此我们的探究过程就结束了吗?

师生活动:教师指出上述结果是在α≠β+2kπ(k∈Z)的前提下得到的,还需验证α=β+2kπ(k∈Z)时等式是否成立.经验证,特殊情况下等式依然成立.因此,当α,β为任意角时,都有cos(α-β)=cosαcosβ+sinαsinβ.

设计意图:在该环节,引导学生分类讨论,体现数学证明的严谨性.同时,让学生知道平面直角坐标系和单位圆在解决三角函数问题中的重要作用,而且证明过程环环相扣,体现了数学的逻辑性,有利于培养逻辑推理核心素养.

3.4 牛刀小试,加深理解

问题5利用两角差的余弦公式求cos 15°的值.

引导学生通过15°=60°-45°和15°=45°-30°两种方式求解,具体过程如图4.

图4 该题对应的教学PPT(截取)

设计意图:帮助学生掌握两角差的余弦公式的应用,拓展数学思维,体会角拆分的多样性决定了变换的多样性,但是最后都殊途同归.

追问:现在能解决“求电视信号发射塔塔尖到地面的距离”问题吗?

师生活动:学生计算,教师播放PPT展示答案.

3.5 深入思考,更新认知

问题6问题5中分别令α,β为特殊值来求得cos 15°的值,能否令α,β为其他形式,从而得到一些公式?

师生活动:教师提示,若令β=-β,则可以得到cos[α-(-β)]=cos(α+β)=cosαcosβ-sinαsinβ,这个公式叫做两角和的余弦公式;还可以令β=-α,则可以得到cos[α-(-α)]=cos 2α=cos2α-sin2α,这个公式是二倍角的余弦公式.给出课后思考题——利用今天所学的两角差的余弦公式推导剩下的两角和与差的正弦、余弦、正切公式以及倍角公式.

设计意图:帮助学生理解α,β的任意性,同时理解公式不仅能正用、逆用,还能变形用.

3.6 课堂小结,巩固知识

问题7本节课你学到了哪些知识?

(1)两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ.

(2)体会到了平面直角坐标系、单位圆在解决三角函数问题中的便利性.

(3)解决数学问题的一些思想和方法:转化与化归、由特殊到一般、分类讨论、数形结合.

4 教学反思

4.1 反思学生

学生虽有一定的认知基础,但在单位圆中证明两角差的余弦公式,容易犯思维不严密的错误.教学时,需要引导学生正确表述终边与单位圆的各个交点,找到正确的等量关系,再结合两点间距离公式计算差角终边与单位圆交点间的距离并化简.

4.2 反思教学

本节课的主要流程为“创设问题情境—抽象数学问题—形成猜想—验证猜想—得出结论—解决问题—深化结论”,以问题链的形式驱动学生思考,以问题情境和学生的旧知(诱导公式)为出发点,利用研究三角函数的常用工具——平面直角坐标系和单位圆,不断探究,自然“生长”出新的知识点——两角差的余弦公式,然后回归到最开始的问题情境解决问题,最后深化主题,将公式的变形应用留作课后思考题,引发学生的进一步思考.整个教学过程让学生发现问题、分析问题、解决问题,其间渗透了数学思想方法,培养了学生数学抽象、逻辑推理、数学运算核心素养.