贝叶斯结构方程模型的原理及应用

乔欣宇 冯咏琳 潘俊豪

（中山大学心理学系，广州 510006）

1 引言

在心理学和管理学等领域，研究者通常使用问卷测量人格和智力等不能直接观测的潜变量。针对这些变量，研究者可以使用潜变量建模的方法进行统计分析。用于反映潜变量的若干个可观测变量，如问卷中的多个测量条目，被称为外显变量。基于结构方程模型的方法，研究者可以分析潜变量之间的关系。结构方程模型在建模分析过程中考虑了外显变量的测量误差，可以获得更准确的变量间关系的估计。常用的验证性因子分析模型、中介效应分析模型和增长曲线模型等都可以使用结构方程模型的形式表征。

结构方程模型的估计主要有频率学派方法和贝叶斯方法两类。贝叶斯结构方程模型是贝叶斯估计在结构方程模型中的应用，在2012年由Muthén和Asparouhov提出，是相对于传统极大似然方法更加灵活的一种新方法。van de Schoot等（2017）的统计结果显示，自2012年以来，贝叶斯结构方程模型得到了越来越多应用研究者的青睐。

本文首先简单介绍贝叶斯分析的基本概念和优势，随后针对贝叶斯结构方程模型估计中的先验设置、敏感性分析、后验分布的计算、模型收敛判断以及模型拟合评估等问题进行基本的介绍，最后采用一个例子演示贝叶斯结构方程模型的建模过程，有助于国内心理学研究者了解贝叶斯结构方程模型在处理交叉载荷、局部依赖性和小样本等问题的建模优势，并将其用于解决自己的研究问题。

2 贝叶斯结构方程模型

2.1 贝叶斯结构方程模型的基本概念

对比传统的频率学派的方法（如极大似然估计方法），贝叶斯估计方法的优势在于可以在参数估计的过程中结合已有的知识或背景信息。基于贝叶斯估计框架，研究者可以得到模型未知参数的分布，而非具体的点估计值。贝叶斯估计方法与传统的频率学派的方法的本质区别在于如何定义模型中的未知参数。

频率学派使用样本估计参数对总体参数进行估计，将模型的待估计参数视作常数，基于模型得到的参数点估计值在最大程度上代表样本数据，被认为是总体参数的最佳估计值，不同模型得到的参数的估计值不同（王孟成等,2017;Depaoli,2021）。在使用频率学派的方法时，研究者使用标准误或者置信区间量化参数点估计值不确定性。

与频率学派的方法相同，贝叶斯估计方法也认为样本数据随机来自一个特定分布的总体。但不同的是，贝叶斯估计方法认为参数是随机的，研究者可以通过先验分布表示参数取不同值的可能性（王孟成等,2017;Depaoli,2021），并基于参数的后验分布得到贝叶斯95%可信区间。贝叶斯可信区间的解释与频率学派的方法不同，它被解释为该区间包含参数总体真值的可能性（Depaoli,2021）。

贝叶斯定理是贝叶斯估计方法中的一个重要部分，对于观测到的样本数据y以及模型参数θ，贝叶斯定理如公式（1）所示，其中p（θ|y）表示在该样本数据中，模型参数值出现的概率，即参数的后验概率；p（y|θ）表示该参数值下的样本数据出现的概率；p（θ）表示该参数的先验概率信息，反映了在总体样本中，参数不同取值的可能性。

在贝叶斯估计中，研究者需要基于已有的信息对参数的分布形态和可能的取值范围进行估计，即设定模型参数的先验分布以及相应的超参数。基于公式（1），研究者可以得到参数的后验分布，并基于后验分布的均值、中位数或众数等得到参数的后验点估计值。

以包含p个测量条目和q个潜因子（p>q）的验证性因子分析模型为例，具体介绍贝叶斯结构方程模型。该验证性因子分析模型如公式（2）所示。

其中yi为代表p×1的连续观测数据向量；μ为表示p×1的截距向量；Λ为一个p×q的因子载荷矩阵，表示观测变量与潜变量之间的关系；ωi表示一个q×1的因子分数向量；εi为一个p×1的测量误差（残差）向量，服从均值为0，方差为Ψ的多元正态分布。在传统频率学派估计方法中，交叉载荷以及残差协方差参数被严格限制为0，因此，Ψ为一个对角矩阵，Λ中一个条目仅对应一个因子。

在贝叶斯结构方程模型中，研究者可以将根据已有理论或者研究结果为验证性因子分析中的未知参数θ=（μ,Λ,Ψ,ω）设定有信息的先验分布、弱信息先验分布或方差很大的无信息先验分布，并结合样本信息以及先验信息使用马尔科夫链蒙特卡洛算法（Markov Chain Monte Carlo;MCMC）估计方法得到未知参数的后验分布。

2.2 贝叶斯结构方程模型的优势

对比频率学派的估计方法，贝叶斯结构方程模型可以有效估计参数较多的复杂模型以及释放严格的模型假设。例如，在传统的极大似然方法中，不重要的交叉载荷或者残差协方差参数通常都被严格固定为0。而这种严格的限制一方面并不能真实反映实际的测量情景，另一方面也可能会导致模型拟合不佳以及参数估计不准确（Asparouhov &Muthén,2009;Marsh et al.,2013）。已有研究者指出，这种针对交叉载荷以及残差协方差参数的严格限制是不合理的，即使在一个单维的量表中，题目之间仍然可能存在除共同的潜变量外的其他因素导致条目之间存在较小的相关关系（Zyphur&Oswald,2013）。如 Golay等（2013）使用贝叶斯结构方程模型自由估计了被严格限制为0的交叉载荷参数，结果发现，与4因子结构和高阶模型相比，包含5个因子加上一般智力因子的直接分层CHC模型（Cattell-Horn-Carroll model，CHC）更能代表韦氏第四版儿童智力量表的结构。Guo等（2019）的文章使用了 CFA、以及针对残差协方差参数设置先验的 BSEM（Bayesian Structural Equation Model with Residual Covariance Priors,BSEM-RC）方法重新拟合了大五人格问卷，研究结果发现使用BSEM-RC方法所得到的因子间的相关更低。因此，有必要对可能存在的交叉载荷以及残差协方差参数进行建模。

传统的频率学派的估计方法处理该问题时存在较多局限，如使用模型修正指数方法一次只能修正一个参数，如果模型中存在多个交叉载荷或残差协方差参数，使用该方法较为繁琐且耗时较长，模型修正结果依赖模型中的参数修正顺序及数量，且没有一个较为明确且通用的停止模型修正的规则，研究者通常基于自己的主观经验确定是否停止修正（Hill et al.,2007）。此外，如果释放较多的参数自由估计，模型可能无法识别，从而不能进行参数估计，导致不能得到结果（Asparouhov et al.,2015）。

而贝叶斯结构方程模型在处理该问题上具有一定的灵活性。它通过设置均值为0、方差较小的先验，放宽将不重要的参数严格设置为零的假设，如允许小交叉载荷或残差协方差的出现，并允许这些参数自由估计，尝试解决在传统方法下模型的限制条件过于严格的问题，兼顾了模型的可识别性与灵活性（Muthén&Asparouhov,2012）。相较于传统频率学方法，这种灵活性使得贝叶斯方法能够处理更加复杂的数据类型和模型，比如数据缺失和残差动态结构方程模型等。此外，贝叶斯结构方程模型也可以得到关于交叉载荷参数以及残差协方差参数的后验分布信息。

此外，贝叶斯结构方程模型在小样本中的表现更好，有利于缓解统计时样本量不足的问题。传统极大似然估计通常假设需要大样本，Lee和Song（2004）的研究发现，当对结构方程模型使用极大似然估计时，样本量与模型参数数量的比值需高于5:1时才能得到准确的参数估计；而实际应用中对样本量的要求往往更加严格，可能需要样本量与模型参数数量的比值达到10:1或20:1。而贝叶斯分析不像频率学方法那样假设大样本，在相对较小的样本量下也能得到比较高的检验力（Lee &Song,2004;van de Schoot et al.,2015）。并且与先验信息相结合是贝叶斯估计的一大亮点，先验信息和样本数据信息共同影响参数的后验分布。小样本情况下，样本数据提供的信息较少并存在抽样误差，而对感兴趣的参数设置具体的先验信息可以为模型估计提供一部分信息，且此时先验信息对参数后验分布的影响程度强于样本信息，从而解决有偏的参数估计问题和低检验力的问题（McNerish,2016;van de Schoot et al.,2015;Zondervan-Zwijnenburg et al.,2019）。

Smid等（2020）系统综述了贝叶斯结构方程模型在小样本在参数估计上相对频率的优势。样本量与模型未知参数数量的比值小于2:1时通常被认为是小样本。综述结果发现当样本很小时，频率方法确实可能导致严重的有偏估计和不收敛的解的问题，而贝叶斯估计可以是一个可行的替代方法。具体而言，贝叶斯估计相比频率估计表现出更优的覆盖率和检验力，在结构参数的后验分布点估计上也有更准确的表现。但是作者也强调研究者在使用先验解决小样本问题时最好不要使用软件的默认无信息先验。因为默认先验可能导致有偏的方差参数估计，而这个问题只能通过结合先验信息来解决。研究者应该更加积极地思考先验超参数，设置有信息先验以解决小样本带来的问题。

总的来说，贝叶斯方法对样本量的要求更低，在小样本条件下能够避免严重的参数估计偏差，能够处理更加复杂的数据，可以分析传统频率学派下无法实现的复杂模型，能够提供更多关于参数估计和模型拟合的信息（张沥今等,2019;McNeish,2016;Muthén &Asparouhov,2012;Smid &Winter,2020）。此外，BSEM建模可以检测传统的CFA模型所忽略的交叉载荷与残差协方差问题，同时避免了由于估计参数较多、模型过于复杂而不可识别的难题（Guo et al.,2019）。

与贝叶斯结构方程模型处理模型中的交叉载荷参数、残差协方差参数严格为0的假设的思路一致，针对多组结构方程模型，研究者同样可以对参数的跨组差异值设置合适的先验（如均值为0，方差较小的正态分布），从而放宽在多组结构方程模型中参数严格跨组不变的限制，得到更为准确的参数估计结果（Asparouhov &Muthén,2014）。张沥今等（2019）的文章中介绍了其他类型的贝叶斯结构方程模型，宋琼雅等（2021）的文章针对贝叶斯渐近测量不变性，详细介绍了该方法的原理及优势，感兴趣的读者可以参考他们的文章深入了解贝叶斯结构方程模型。

3 贝叶斯结构方程模型中的先验设置

模型中未知参数的先验分布是贝叶斯结构方程模型中的重要组成部分。先验信息包含了先前的结论或前人研究的经验与结果，反映了研究者对待估计参数的了解程度，先验信息的丰富程度可以通过不同的超参数设定呈现。常见的超参数有先验分布均值和先验分布方差，前者反映了研究者基于已有的研究结果和理论知识对特定参数所确定的估计值，后者反映了研究者对其估计均值的相信程度，方差越小表示研究者对先验均值的信心越多（Liang et al.,2020）。

van de Schoot等（2013）认为可以在研究理论、先验信息的丰富程度以及研究者对先验的确信程度的基础上为参数设置不同类别的先验分布。基于所包含的信息程度，先验可以分为有信息先验、弱信息先验和无信息先验。在传统方法中，每个研究的假设总是基于当前研究者的信念，而前人研究的结果未能在新的研究中起到最大的指引作用。贝叶斯分析中先验信息与观测数据的结合有效改进了这一点，真正将前人研究的结果运用在后续研究的分析之中，体现了知识的累积和与理论的进步，相较于传统方法更具优势（王孟成,毕向阳,2018;Muthén &Asparouhov,2012）。

对于贝叶斯结构方程模型中不同的参数，为保证模型可以被识别并估计，研究者在考虑有关模型参数已有信息的同时，对于不同类型的参数通常会选择不同的先验分布形式。Mplus（Muthén &Muthén,1998—2017）和R语言中的blavaan软件包（Merkle &Rosseel,2015）是在进行贝叶斯结构方程模型建模过程中常使用的工具，表1总结了这两个工具中不同参数的默认先验形式与默认先验超参数。

表1 Mplus 与blavaan 软件包中不同参数的默认先验形式与默认先验超参数

对于贝叶斯结构方程模型中的因子载荷、截距、斜率与回归系数，正态分布先验最为常用，表示为N[μ，σ2]，μ其中为平均超参数，决定了先验分布的中心，而σ2为方差超参数，方差越小表明研究者对参数值的确信程度越高，信息量越大，而大方差表明研究者对参数值的确信程度更低，信息量较小。Mplus中默认的超参数设置为N[0，1010]，为无信息先验；blavaan软件包相较于Mplus中的默认先验形式有所不同，测量截距的默认先验为N[0，1000]，截距、载荷以及回归系数的默认先验则为N[0，100]。

对于贝叶斯结构方程模型中的方差协方差矩阵，常用的先验形式为逆Wishart分布，可以表示为IW[s，df]，即当存在q个因子（测量条目）时，s是一个大小为q×q的正定矩阵，df则是一个表示自由度的整数，通过改变df的大小可以为先验分布指定不同丰富程度的信息量，df越大表示对先验的确信程度越高（Barnard et al.,2000）。在软件Mplus中，对于连续变量以及类别变量的方差协方差矩阵，所使用的默认先验不同，连续变量的默认先验为IW[0，-p-1]，类别变量的则为IW[0，p+1]，其中p为变量的数量，I为单位矩阵（Muthén &Muthén,1998—2017）。

对于残差方差，常用的先验分布形式为逆Gamma分布，表示为IG[α，β]，其中α为形状超参数，不同的α表示分布曲线形状不同；β为尺度超参数，在α大小不改变的条件下，不同大小的β会使得曲线以等比例放大或缩小。在Mplus中，默认先验为IG[-1，0]。相较于正态分布先验和逆Wishart分布先验的超参数设置，逆Gamma分布先验的超参数设置显得不那么直观。根据Gelman等（2013）的建议，为确定这些超参数的值，可以使用来自先前研究（前人观察样本、前人研究或试点研究）的信息，以通过先前研究样本量的作为超参数α，而超参数β可以被计算为先前研究样本量的乘以先前研究的方差估计。假设研究者在试点研究中收集了20个参与者的数据并对模型进行评估，对于某个条目的残差方差估计为2，这时超参数，超参数，即可以在后续研究中对该条目的残差方差设置IG[10，20]的先验。如果研究者对于先验不是十分确信，可以通过用较小的值代替先前研究的样本量来增加先验中的不确定性，如将α设置为编码样本量里的，而将β设置为编码样本量的乘以先前研究的方差估计。根据这种情况，在上述例子中，超参数，超参数，可以在后续研究中对该条目的残差方差设置IG[5，10]的先验。对于残差方差的倒数形式，即残差精度，常用的先验形式则为Gamma分布，表示为G[α，β]，α和β同样分别为形状超参数与尺度超参数。

对于相关系数，通常会为其设置均匀分布先验，表示为U[l，u]，其中超参数l和u分别表示上界和下界，这些超参数通常以±1为界（van Erp et al.,2018）。除Mplus与blavaan外，还有如Stan，Amos，WinBUGS等软件可以实现贝叶斯结构方程建模，其默认先验的设置可以参考van Erp等（2018）的研究。

综上，在各种软件中一般都默认是无信息先验，当对参数设置该类型先验时，参数的后验分布更多取决于数据中包含的信息，这使得研究者们不用为参数的先验设置而烦恼，提供了便捷使用贝叶斯结构方程模型的方式（Smid&Winter,2020;van Erp et al.,2018）。根据van de Schoot等（2017）的综述，在1990年到2015年的近25年中，研究者们在使用贝叶斯方法进行心理学领域研究时经常依赖于软件的默认先验（26.3%），在已发表的文章中使用无信息或弱信息先验的研究占42.1%。然而，也有很多研究者指出，使用默认的无信息先验并不能最大程度地发挥贝叶斯方法相较于传统方法更加灵活的优势，因为前人研究的背景知识并不能有效通过默认先验纳入当前分析，并且在小样本情况下，软件的默认先验分布可能并不合适，希望默认先验能最大限度体现数据信息的想法可能会在小样本中导致参数估计存在严重偏差（Smid &Winter,2020;Smid,McNeish,et al.,2020;van de Schoot et al.,2018）。

基于以上使用默认先验可能导致的偏差，许多研究都推荐在贝叶斯结构方程模型中对部分参数设置有信息的先验（Depaoli,2014;Gelman et al.,2013;McNeish,2016;Smid,Depaoli,et al.,2020）。Smid和Winter（2020）为研究者提供了选择正确先验的指导，了解未知参数值的合理范围是避免使用不合理先验的关键。研究者可以考虑从前人文献的结果中提取信息，或是考虑研究中让所使用的问卷与量表能够得到分数的合理范围，亦或是询问相关领域专家的专业建议，从而为参数设置正确的先验分布。例如，根据Muthén和Asparouhov（2012），对于正态分布先验，设置均值为0的小方差正态分布先验能够更加准确地反映出实质性的理论，当对于因子载荷设置N[0，0.01]的先验分布时，因子载荷后验分布的95%可信区间将在-0.2与0.2之间；而对于逆Wishart分布先验，推荐选择自由度df≥p+4，其中p为变量的数量，以保证获得可识别的后验分布。当对于残差协方差，设置IW[l，p+6]的先验分布，在该先验下残差协方差的两个标准差范围为-0.2至0.2。

在使用贝叶斯结构方程模型分析数据时，研究者需要谨慎选择先验，因为不同的先验设置可能会影响MCMC算法的性能；错误的先验设置甚至会导致得到具有严重偏差的后验分布结果，影响参数估计的准确性与模型的收敛率（Baldwin &Fellingham,2013;Depaoli&Clifton,2015;MacCallum et al.,2012;van Erp et al.,2018;Yuan &Mackinnon,2009;Zondervan Zwi-jnenburg et al.,2017）。例 如，Tong和Ke（2021）的研究结果表明，在贝叶斯非参数增长曲线建模中，信息量水平不同的精度参数先验会影响模型的收敛速度、模型估计以及计算时间。Lee等（2020）发现，在使用贝叶斯潜类别分析时，如果选择了与参数的真实分布差异显著的有信息先验，可能会导致一类错误率升高。此外，偏离参数真值分布的先验还会对贝叶斯模型拟合指标判断模型拟合情况的表现与选择正确模型的能力造成影响，且不同的模型拟合指标对先验分布的敏感性存在差异，越来越多的研究关注到频率学派中模型拟合指标的截断值是否依旧适用于贝叶斯方法（Liu et al.,2021;Winter &Depaoli,2022）。

因此，尽管与先验分布相结合使得贝叶斯结构方程模型相对于传统模型具有更加灵活的优势，但如何设置参数的先验分布是使用该方法最大的挑战之一（van Erp et al.,2018）。对于判断在贝叶斯结构方程模型中选择的先验是否合适，Smid和Winter（2020）提出了四种方法：

一是计算有效样本量，即在后验链中有效独立抽取的样本数量，当有效样本量小于1000时，可能说明先验的选择存在问题。

二是看轨迹图，当轨迹图中多条链大部分重合时，可能可以说明先验的选择是合适的，但依旧要注意后验分布中是否存在现实中不可能出现的数值，在这种情况下即使多条链出现了重合，但依旧可能表明先验是不合适的，而当多条链之间完全缺乏重合时，很有可能说明选择的先验是非常不合适的。

三是比较先验分布、似然分布与后验分布，当他们之间存在实质性差异时，需要注意设置的先验是否合适，当似然与先验偏差很大时，尤其是在小样本的情况下，后验分布可能受先验分布影响很大，从而导致结果的偏差。

四是检查后验标准差与95%的可信区间，当标准差过大与可信区间范围过宽时，先验的选择可能存在问题。此时，研究者可以使用敏感性分析，进一步了解先验分布对结果的影响，从而选择正确的先验（Smid &Winter,2020）。当研究者想要探讨某个特定的先验的影响时，可以对该先验的均值超参数或方差超参数进行敏感性分析，具体来说可以对增大或者缩小均值超参数或方差超参数，得到具有不同均值或方差超参数的先验，并使用这些不同的先验进行参数估计；随后，研究者可以通过比较几个不同先验下模型的收敛率、计算速度、效应量、模型拟合指标的表现以及模型参数估计结果，从而检查先验的超参数设置对于参数的估计是否具有实质性的影响（Depaoli &van de Schoot,2017;Liu et al.,2021）。

van Erp等（2018）根据模拟研究的结果建议，如果希望在研究中使用默认先验，可以考虑包含软件默认无信息先验与多个水平的弱信息先验的敏感性分析。如果敏感性分析结果显示在不同先验下模型分析的结果十分稳定，可以认为使用默认先验得到的结果是可靠的；如果在研究中希望使用有信息先验，可以对有信息先验与默认无信息先验进行敏感性分析，比较不同先验分布下模型的结果以考虑有信息先验分布下的研究结果是否可靠（Depaoli&van de Schoot,2017）。R语言中的MplusAutomation软件包（Hallquist &Wiley,2018）可以通过调用Mplus生成多个先验条件下贝叶斯结构方程模型的输入文件，并对其进行运算，得出模型分析的结果，可以有效运用于完成先验的敏感性分析。

4 贝叶斯估计中后验分布的计算

研究者主要借助MCMC算法估计后验分布，该方法通过在参数的概率空间中随机重复抽样从而得到参数的近似分布（Gelfand &Smith,1990）。MCMC算法可以分为马尔科夫链和蒙特卡洛两个部分。其中马尔科夫链过程确定每一次随机抽样的规则，即下一次迭代中参数估计值仅依赖当前迭代中的参数估计值，而与之前的迭代过程无关；蒙特卡洛方法是通过在分布中抽样的方式确定模型参数的近似值及其后验分布，蒙特卡洛抽样过程中的样本均来源于特定的马尔科夫链（Depaoli,2021;Van Ravenzwaaij et al.,2018）。

MCMC在不断的迭代过程中，针对每一个参数都会形成马尔科夫链，而链中的每一个值都是基于蒙特卡洛抽样方法实现的（Depaoli,2021）。具体而言，在进行MCMC的过程中，研究者首先需要给出模型参数的初始值，基于样本数据、参数的先验信息以及模型参数的初始值，在每一次迭代中，研究者可以基于蒙特卡洛抽样方法得到参数当前的估计值；基于当前迭代中的参数估计值，研究者可以得到下一次迭代中的参数估计值，多次重复该过程，每一次迭代中得到的参数估计值最终构成了稳定的参数后验分布。在构成参数后验分布的过程中，并不是每一次迭代中基于蒙特卡洛得到的参数估计值都会被保留用于构成参数后验分布。研究者可以使用不同的算法调整是否保留基于当前的参数估计值确定的下一次迭代中的参数估计值的规则。常用的两种算法为Gibbs抽样和MH算法（Metropolis-Hastings algorithm;Depaoli,2021），具体关于该算法细节的介绍可以参考Bos（2004）以及Depaoli（2021）。

5 贝叶斯结构方程模型的收敛判断

在使用MCMC算法进行贝叶斯估计时，随着迭代的增加，模型参数的后验分布逐渐趋向稳定，即模型达到收敛。判断模型参数迭代收敛是评估模型后验参数估计的重要问题之一。在实际应用中，研究者可以基于多个不同的评价指标判断贝叶斯结构方程模型是否已经达到收敛。

（1）收敛图或踪迹图。当样本的参数估计在踪迹图中的波动较小，相对稳定时，表示该参数已经达到收敛。这种基于踪迹图的方式较为直观，因此并不能说明是否该参数真正达到了收敛。但总的来说，该方法可以作为模型参数尚未达到收敛的标准（Mengersen et al.,1999）。如果模型参数的踪迹图表现出较大的波动或者出现极端值，则该参数有较大的可能性尚未达到收敛。

（2）Geweke收敛诊断。该收敛诊断方法主要用于判断单条链的第一部分是否与该链的最后一部分之间存在显著差异，常用于判断单条链是否达到了收敛。研究者需要设定一定的迭代比例作为链的开始以及链的结束。Geweke（1992）最早指出可以比较链前10%以及后50%的部分的结果进行收敛性判断。研究者可以基于实际情况调整用于比较的链的比例，确保用于比较的每一个部分足够大从而保证基于两次抽样过程得到的均值彼此独立。基于一条链的两个部分彼此独立的假设，研究者可以使用z检验的方法判断是否达到收敛，即若z检验显著则说明该参数的迭代并未达到收敛（Smith,2007）。研究者可以使用R工具包coda完成Geweke收敛诊断（Plummer et al.,2006）。

（3）潜在尺度缩减因子（Potential Scale Reduction,PSR）或Gelman-Rubin法。PSR通过比较参数估计的链内和链间的变异性判断参数是否达到收敛，当链间的变异性小于链内的变异性时，不同链得到的参数估计结果接近一致，则说明该参数估计达到收敛（Gelman &Rubin,1992）。针对PSR，Mplus软件使用的默认标准为1.05，当PSR小于1.05则认为模型达到收敛（Muthén &Muthén,1998—2017）。Vehtari等（2019）的文章中针对该指标的使用提出了更多的建议。

（4）自相关图。在MCMC算法中，基于马尔科夫链，每一次的抽样过程仅依赖前一次的抽样。理论上每连续两次抽样之间都会存在自相关系数，而非连续两次抽样之间则相互独立。但是在实际场景中，该假设很难得到满足。因此，研究者通常会计算一定抽样间隔的抽样相关。当自相关数小于0.1，则认为抽样样本之间彼此独立（Depaoli,2021）。

当模型在迭代过程中尚未达到收敛时，研究者可以通过修改模型参数估计的初始值以及增加迭代次数的方式提高模型的收敛。此外，当模型的先验设置不正确时，模型参数也会存在不收敛的情况，因此研究者也可以基于实际情况对模型参数的先验做出调整。研究者可以使用R工具包coda绘制参数的自相关图（Plummer et al.,2006）。

6 贝叶斯结构方程模型的拟合评估和模型选择

在贝叶斯结构方程模型的模型拟合评估方面，贝叶斯近似拟合指标和模型选择指标的数量以及关于这些指标的研究深入程度都远远不及频率学方法（West et al.,2012）。对于贝叶斯模型拟合指标，许多研究在早期仅局限于后验预测p值（Posterior predictivep-values,PPp,Gelman et al.,1996）。与传统的显著性检验的p值不同，PPp中的p值是指观测数据产生的卡方值比模型生成的样本数据产生的卡方值小的比例，该值接近0.5则表示模型拟合越好，越偏离0.5则表示模型拟合越差，研究者通常使用0.05作为模型评估的标准，若PPp值小于0.05，一般认为模型拟合不佳。相应地，研究者同样可以获取后验预测检验的95%区间，用于表示样本数据与模型生成的数据之间的统计检验量差异，当该区间的下限为负数，且0位于该区间内时，则表示模型拟合良好（Muthén &Asparouhov,2012）。

Hoofs等（2018）首次提出了近似均方根误差的贝叶斯变体，并命名为贝叶斯近似均方根误差（Bayesian root mean square error of approximation,BRMSEA），Garnier-Villarreal和Jorgensen（2020）由此进一步拓展了贝叶斯框架下的近似拟合指标，包括贝叶斯比较拟合指数（Bayesian Comparative Fit Index,BCFI）、贝叶斯Tucker-Lewis指数（Bayesian Tucker-Lewis Index,BTLI）。对于新提出的贝叶斯近似拟合指标，由于其与使用极大似然方法的近似拟合指标具有相似的表现，研究者推荐使用传统近似拟合指标的截断值作为贝叶斯框架下的近似拟合指标对模型的评价标准（Asparouhov &Muthén,2021）。因此，根据Hu和Bentler（1999）提出的极大似然方法的近似拟合指标的截断值，可以使用BRMSEA=0.06,BTLI=0.95，BCFI=0.95作为截断值。贝叶斯模型拟合指标相对于传统模型拟合指标的一个优势在于可以计算模型拟合指标的可信区间，而不是单纯地使用点估计进行模型拟合判断，这可以给判断模型拟合是否良好提供更丰富的信息（Asparouhov &Muthén,2021）。我们可以通过比较贝叶斯近似拟合指标的可信区间和截断值来判断模型拟合是否良好。当截断值高于可信区间的最大值（对于BRMSEA而言是截断值低于可信区间最小值）时，可以判断模型拟合不佳；当截断值低于可信区间的最小值（对于BRMSEA而言是截断值高于可信区间最大值）时，则判断模型拟合良好；当截断值被可信区间所包含，则不能明确判断模型拟合不佳或模型拟合良好。举例来说，假设BCFI的截断值为0.95。（1）当BCFI的点估计为0.892时，可信区间为［0.873,0.902］，截断值高于可信区间的最大值，BCFI表明模型拟合不佳；（2）当BCFI的点估计为0.961，可信区间为［0.958,0.976］，截断值低于可信区间的最小值，BCFI表明模型拟合良好；（3）当BCFI的点估计为0.950，可信区间为［0.872,0.963］，截断值被可信区间所包含，则不能明确判断模型拟合不佳或模型拟合良好。

在贝叶斯结构方程模型框架下，模型选择指标的数量相对更多，常用的指标有偏差信息准则（Spiegelhalter et al.,2002）、贝叶斯因子（Bayes factor,BF;Kass &Raftery,1995）、贝叶斯留一法（Bayesian leave-one-out,LOO;Gelfand et al.,1992）等，Lu等（2017）在CFA的框架下详细对比了这些指标。

对于上述贝叶斯模型选择指标以及贝叶斯近似拟合指标在模型选择过程中的应用，各指标也存在不同的截断值来表明两个模型之间存在显著差异。对于DIC，在模型比较中，两个模型中DIC更小的模型拟合得更好，通常会使用两个模型的DIC相减，得到ΔDIC。Cain和Zhang（2019）一项研究的结果表明，选取ΔDIC=7为截断值能较好降低选择错误模型的概率。

对于贝叶斯近似拟合指标在模型选择的应用，目前的研究依旧参照的是传统极大似然方法下近似拟合指标的截断值。但是由于近似拟合指标被用于模型选择的情况相较于模型选择指标更少，不同研究者针对不同近似拟合指标给出了模型选择的不同截断值。有研究者认为当CFI的差异值大于0.005，TLI的差异值大于0.005和RMSEA的差异值大于0.010时，则说明模型之间存在显著差异；但也有研究者认为当CFI和TLI的差异值大于0.01，RMSEA的差异值大于0.015时，则说明模型之间存在显著差异；并且在样本量的不同水平，应该选取不同的截断值以保持近似拟合指标进行模型选择判断的敏感性（Chen,2007;Sokolov,2019）。

贝叶斯框架的模型拟合指标已被证实与传统极大似然方法中的近似拟合指标合理近似，并已经被Asparouhov和Muthén（2021）运用在软件Mplus中。由此，越来越多的研究者关注贝叶斯框架下的近似拟合指标，并展开了关于先验设置敏感性的研究（Cain &Zhang,2019;Liang,2020;Winter &Depaoli,2022）。目前，关于近似拟合指标进行模型选择的研究较少，对于贝叶斯近似拟合指标的截断值尚存在争议。McNeish和Wolf（2021）的研究基于模拟的方法来针对特定数据和结构构建特定的验证性因子分析模型动态截断值，并开发了一个RStudio附带的Shiny应用程序（https://dynamicfit.app/），目前也可以通过名为“dynamic”的R包计算不同验证性因子分析模型的动态截断值，给研究者提供了能获得更加精确的频率学派结构方程模型框架下的模型拟合指标截断值的方法。未来研究或许可以拓展该研究的发现，进一步探索用于贝叶斯近似拟合指标的动态截断值。然而，尽管贝叶斯方法如今在心理学领域仍未如频率学方法一般得到广泛应用，但其优点已在各种研究中逐渐显现，进一步了解和探索新提出的贝叶斯模型拟合指标进将是普及使用贝叶斯结构方程模型的重要课题与方向。

7 示例：使用贝叶斯结构方程模型处理模型中的交叉载荷问题

在本研究中，我们将使用一个实证数据展示和说明贝叶斯结构方程模型针对交叉载荷参数的建模过程。本文用于展示的软件为Mplus，该软件为最常用的潜变量建模软件之一。其他的可以使用贝叶斯估计方法构建结构方程模型的软件有WinBUGS、Stan、R软件包blavaan等，关于这些软件的介绍可以参考张沥今等（2019）的文章。

7.1 数据介绍

本研究选用 Holzinger 和 Swineford的经典数据集进行展示，原有Holzinger和Swineford的智力测试中共包含了26个变量，本研究选择了包含9个变量的数据子集。该数据子集同样是R 语言的lavaan工具包和 blavaan工具包中的内置数据。该数据集包含了来自Pasteur 学校和Grant-White 学校的 301 名七年级和八年级儿童的智力测试分数，为避免学校不同带来的影响，本研究仅考虑来自Grand-White学校的145名儿童的数据。

智力测试子集中的九个变量分别为视觉感知、立方体、菱形、短文理解、句子填空、词义理解、加法、点计数与直曲线大写字母，其中前三个变量用于测量空间能力，中间三个变量用于测量语言能力，最后三个变量用于测量反应速度，具体的模型如图1所示。该训练子集包含了来自Pasteur和Grant-White两所学校的301名七年级和八年级儿童的智力测试数据。该智力子集的Cronbach’s α为0.760，各潜变量的Cronbach’s α分别为0.626、0.883、0.688。

为更加直观地体现贝叶斯结构方程模型的灵活性，本研究同时展示使用频率学派的极大似然估计方法和贝叶斯结构方程模型得到的结果。在贝叶斯结构方程模型建模估计的例子中，本文着重体现贝叶斯结构方程模型在处理交叉载荷参数问题上的优势，因此，针对主要的因子载荷参数以及因子间相关参数，均使用Mplus软件的默认先验；针对交叉载荷参数，以均值为0，方差为0.01的正态分布先验N（0,0.01）为例展示建模过程及模型参数估计结果。随后将展示默认先验以及强信息先验的结果，以模拟在实际研究中研究者进行敏感性分析的过程。

7.2 使用Mplus 进行贝叶斯结构方程模型建模

在使用Mplus进行贝叶斯结构方程模型建模时，研究者在进行模型设定前，需要在ANALYSIS语句中先设定模型使用的估计方法以及方法的细节。如针对本研究的例子，需要使用贝叶斯估计方法进行贝叶斯结构方程模型建模，则对应的估计方法需要选择BYAES，对应的语句为“ESTIMATOR=BAYES”。当研究者使用频率学派的方法进行估计时，对应的估计方法可以选择极大似然估计方法或经过均值和方差校正的最小二乘法等。针对贝叶斯估计方法，研究者同样需要设置模型中的马尔科夫链的数量和模型迭代次数等信息。

7.3 结果解释及报告

由于使用贝叶斯结构方程模型对数据进行建模的过程中，对比传统的频率学派方法，研究者需要基于已有的经验给出模型中参数的先验信息，且针对模型参数也会存在不收敛以及参数后验分布准确性等问题，因此，图2结合Depaoli（2021）对贝叶斯估计方法的结果报告的建议以及Depaoli 和 van de Schoot（2017）提出的 WAMBS 清单对估计结果的报告步骤进行整理，本文的示例也将参考该过程报告结果。

图2 贝叶斯结构方程模型结果报告流程梳理

（1）样本数据相关的人口学信息。与传统频率学派估计方法的结果报告一致，在报告参数估计结果前，研究者需要报告样本数据的基本信息，如样本量的大小、性别比例、正态分布情况和变量之间的相关信息等。如果对样本数据进行了拆分，如使用一部分被试用于确定模型中参数的先验信息，另外一部分用于估计模型的参数结果；或存在多个样本数据时，研究者需要分别报告多个样本数据的相关信息，以及数据拆分的具体步骤和规则。在本文的示例中，总样本量为145，其中男性被试72人，女性被试73人。变量均不存在严重的非正态情况，峰值范围为2.520～5.164，偏度范围为-0.544～0.721。

（2）贝叶斯结构方程模型估计的软件使用以及相关参数的设置。参数先验信息是贝叶斯估计中较为重要的一部分，研究者在报告贝叶斯结构方程模型的参数估计结果前需要报告不同参数先验设置的理论背景和参数先验设置的细节。本研究的目的在于展示贝叶斯结构方程处理交叉载荷问题时的效果，因此仅对模型中的交叉载荷参数设置先验。考虑到在问卷设置过程中，一般不假设模型中存在交叉载荷的情况，且针对交叉载荷参数常用正态分布作为先验，因此，本研究中针对交叉载荷参数设置均值为0，方差为0.01的正态分布先验，允许交叉载荷参数在［-0.2,0.2］范围内波动。

另外，在报告结果时，研究者需要报告贝叶斯估计中相关参数的设置，如模型中参数估计的初始值、模型迭代次数及模型中MCMC链的数量等。在示例展示中，我们使用Mplus软件中的默认初始值进行估计，并设置2条MCMC链。为保证模型参数估计更加准确，在模型估计中使用50000次固定迭代。

（3）贝叶斯结构方程模型的收敛情况。在实际应用中，研究者可以通过“BCONVERGENCE=0.05;”语句修改PSR收敛判断的标准，其中0.05为Mplus默认值。当PSR<1+CONVERGENCE*factor则表示该参数已经达到收敛。其中factor的取值范围为［1,2］，取值的标准为参数数量（Muthén&Muthén,1998～2017）。当研究者使用单条MCMC链进行估计时，Mplus默认使用第3/4和最后1/4链的迭代结果进行计算。在本文中，BCONVERGENCE使用Mplus默认值。

另外，通过在Mplus的输入input文件（.inp）中，研究者可以使用“PLOT:TYPE=PLOT2;”语句输出参数估计的后验分布结果图；并在对应output（.out）文件中，研究者可以通过PLOT→View Plot查看参数的后验分布、后验参数踪迹图、自相关图和后验预测检验图得到模型的收敛情况。有关基于踪迹图、自相关图等判断模型收敛的介绍可以参考王孟成等（2017）的文章。

以测量条目Y9和因子空间能力之间的交叉载荷参数为例，图3（a）表示该参数的踪迹图。本文仅考虑了两条MCMC链，因此，图中使用黑色和灰色分别表示了不同链的估计结果，其中横坐标表示对应的迭代次数，纵坐标表示后验参数估计值，研究者可以基于踪迹图的方式直观评估两条链的参数估计值是否收敛到相同的、平稳的分布。其中图中最长纵线之前的部分表示burn-in阶段，后半部分的结果用于判断模型是否达到收敛，从图3（a）可以看出该参数逐渐迭代过程趋于平稳。

图3 条目Y9 与因子空间能力之间的交叉载荷参数估计的踪迹图和自相关图

图3（b）为测量条目Y9和因子空间能力之间的交叉载荷参数的自相关图，其中纵坐标表示相关系数大小，横坐标表示不同的迭代间隔次数或步长。如图3（b）所示，随着迭代的增加，自相关系数逐渐低于0.1，趋于0，说明模型收敛良好。结合TECH8的结果显示，当达到2500次迭代时，PSR=1.008，已经达到收敛的标准。这些结果均显示模型的参数估计收敛良好。当模型尚未达到收敛时，研究者可以选择增加迭代次数或修改模型估计的初始值。

（4）贝叶斯结构方程模型模型拟合评估。在进行贝叶斯结构方程模型建模时，Mplus会输出关于模型拟合的相对应的结果，所使用的指标有PPp、CFI、TLI、RMSEA等。在本研究中，模型拟合良好，其中PPp=0.436（后验预测检验95%CI为［-25.85,31.81］）、CFI=0.99、TLI=0.99、RMSEA=0.04。

（5）模型参数估计结果。在模型结果部分，Mplus会基于参数后验分布的中位数得到对应参数的点估计值，并基于后验分布得到参数的95%的可信区间。表2展示了在本研究中，针对交叉载荷参数使用均值为0、方差为0.01的正态先验分布后对应得到的模型因子载荷参数的结果。贝叶斯结构方程模型检测出一个显著的交叉载荷参数。

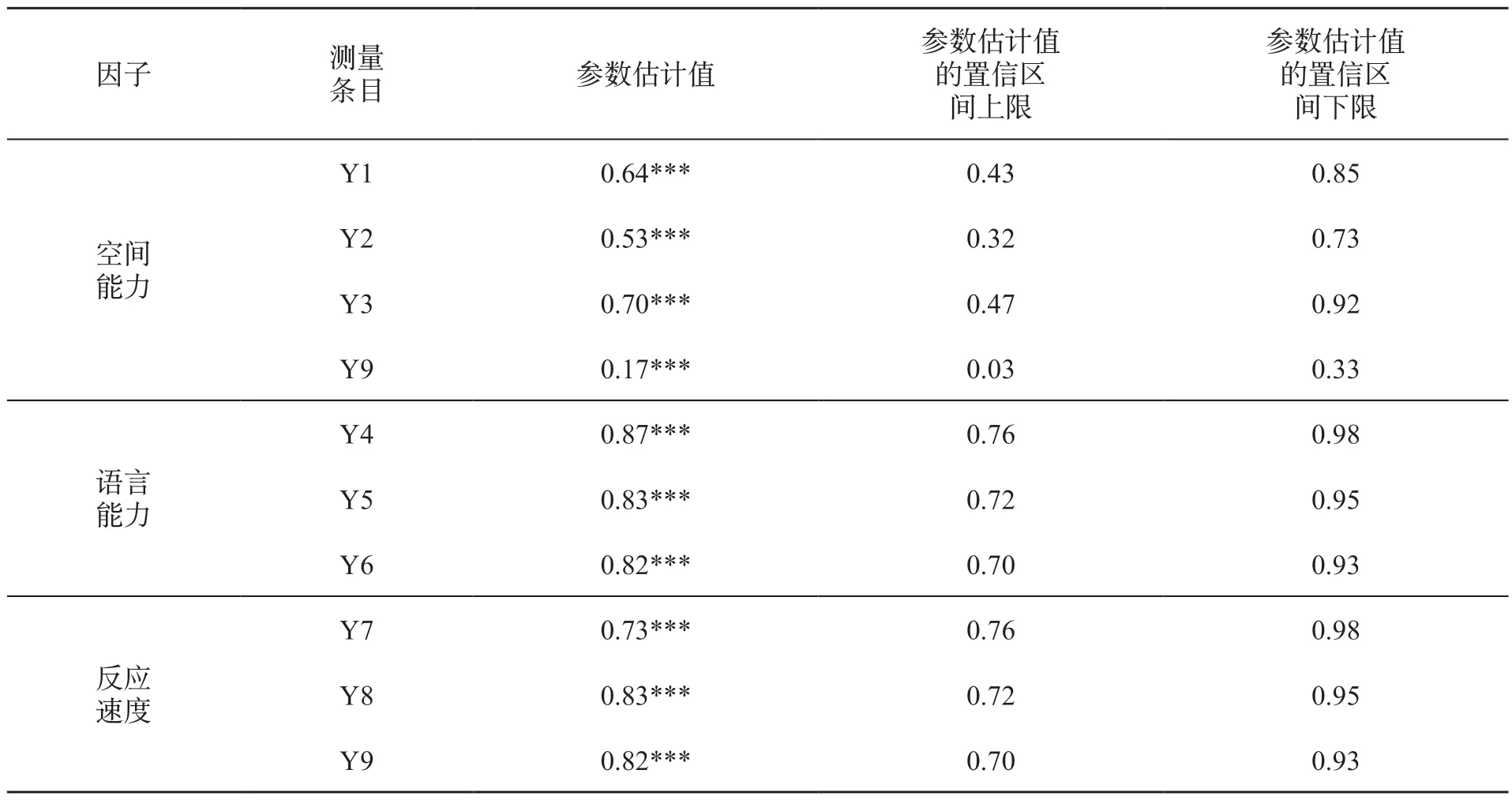
表2 针对于交叉载荷参数设置N（0,0.01）先验的BSEM 模型的因子载荷参数估计结果

7.4 敏感性分析：不同先验的贝叶斯结构方程模型结果

在进行贝叶斯结构方程模型建模时，为进一步避免先验设置错误导致的参数估计偏差，研究者可以进行敏感性分析，比较设置不同先验的模型参数估计结果（Depaoli &Van de Schoot,2017）。为进一步展示敏感性分析及其结果，本文修改了贝叶斯结构方程模型中交叉载荷参数的先验作为展示，分别为：（1）Mplus默认的先验信息；（2）强信息先验，即均值为0，方差为0.0001的正态分布先验，该先验设置交叉载荷参数的变化范围为［-0.02,0.02］。相比均值为0，方差为0.01的正态分布先验，该先验对交叉载荷参数变化范围的限制更高。除交叉载荷参数的先验设置不同外，其他模型设置参数均与均值为0、方差为0.01的正态分布先验时的模型参数设置相同。

数据分析结果显示，当使用Mplus默认的先验设置时，模型中方差协方差矩阵不正定，模型不收敛。当对交叉载荷参数使用强信息先验时，结合参数的踪迹图以及自相关图的结果均显示模型收敛。在模型拟合评估中，PPp=0.023，小于0.05，即该结果显示模型拟合不佳。在模型参数估计中，强信息先验BSEM模型未识别出交叉载荷参数。在强信息先验条件下，该先验条件限制交叉载荷参数在较小的范围内波动，且样本量小，样本数据能为模型参数估计提供的信息相对有限。因此交叉载荷参数估计值多在0.01附近波动。综合来看，虽然强信息先验的贝叶斯结构方程模型达到了收敛的标准，但是拟合不佳，尚未识别出其中可能存在的交叉载荷参数。而这也进一步反映了当处理小样本的情况时，先验条件的设置会对模型的参数估计产生较大的影响，研究者对此需要慎重考虑。

通过对比不同先验的贝叶斯结构方程模型结果发现，先验信息设置对模型的参数估计具有较为重要的影响。且在实际研究中，先验信息是基于已有的理论或结果，存在一定的主观性，有必要尝试使用不同的先验验证结果的稳健性。

7.5 频率学派的验证性因子分析结果

本研究同样使用频率学派的极大似然估计方法对数据进行验证性因子分析，并基于模型修正指数MI释放严格的模型假设，优先修正MI较大的交叉载荷参数，估计可能存在的交叉载荷参数。参考CFI>0.95，TLI>0.95，RMSEA<0.08，SRMR<0.08的模型拟合良好的标准（Hu &Bentler,1999）判断是否停止修正。如果模型拟合良好，则结束修正过程。

具体的模型修正过程及每一次修正后的模型估计结果如表3所示。该结果显示，最终基于模型拟合良好的标准确定的模型中存在一个交叉载荷参数，结果如图4所示，该交叉载荷与贝叶斯结构方程模型得到的结果一致。

表3 使用频率学派极大似然估计方法进行模型修正过程所得到的模型拟合结果

8 讨论

贝叶斯结构方程模型在模型拟合和识别、参数估计、处理复杂模型以及小样本问题中都有较大优势。基于先验信息的设置，研究者可以释放原有传统测量模型中较为严格的参数限制，同时也可以将已有信息整合在当前研究中，从而得到更准确的模型参数估计结果。本研究示例所展示的结果表明，对比传统频率学派的估计方法，贝叶斯结构方程模型可以准确地检测出模型中可能存在的交叉载荷参数，得到相对准确的参数估计结果。

国内学者王孟成等在2017年简要介绍了贝叶斯统计在潜变量建模过程的应用，随后张沥今等（2019）介绍了贝叶斯结构方程模型的方法基础以及常用的贝叶斯结构方程模型的研究现状，为更多研究者了解新的研究工具提供了一定的基础。但截至2023年5月，基于中国知网的检索发现，国内心理学领域有关贝叶斯结构方程模型的应用研究仍相对较少。希望本文可以帮助更多国内心理学研究者了解贝叶斯结构方程模型在处理小样本、严格的模型参数假设和复杂模型等问题上的优势，基本掌握贝叶斯结构方程模型解决实际研究问题的操作。

在贝叶斯结构方程模型建模中，模型参数的先验设置具有一定的主观性，对参数的估计具有一定的影响。本文示例展示的结果同样表明，先验设置可能会导致模型不收敛或者模型参数估计不准确等问题。因此，研究者在实际使用过程中有必要基于已有知识选择多个先验条件建模，从而得到更为稳健的参数估计结果。此外，由于贝叶斯估计方法在对参数的解释上与传统的频率学派的方法存在一定差异，因此不可避免地可能会错误解读模型估计结果。Depaoli和Van de Schoot（2017）提出了WAMBS清单，该清单描述在应用贝叶斯估计时需要重视10个点，主要包括对先验的理解、模型收敛性的检验以及模型估计结果的解释三个方面。研究者在实际进行贝叶斯结构方程模型建模时，也可以参考该清单完善自己的建模过程。

由于不同的软件使用不同的抽样方法进行贝叶斯结构方程模型的参数估计，且当研究者在使用默认先验时，不同软件默认的先验设置不同，这些都会影响最终的模型参数估计结果（Jak et al.,2021;van Erp et al.,2018）。因此，研究者需要注意不同软件可能会导致不同的估计结果。

本文旨在简要介绍贝叶斯结构方程的原理及其在心理学的应用，更多关于贝叶斯结构方程的方法基础、原理以及在Mplus软件上的应用的相关信息，感兴趣的研究者可以参考张沥今等（2019）、王孟成等（2017）、Depaoli和Van de Schoot（2017）的文章以及Depaoli（2021）或王孟成（2014）主编的书籍。