关注问题梯度,提升解题能力——以“一次函数面积问题”教学设计为例

秦 哲

⦿广东省深圳实验学校初中部

面积问题一直是中考的重点和难点,平面直角坐标系中的面积问题往往是几何与函数的综合问题,一般考查学生逻辑思维能力和数学知识的综合应用.学生遇到这类问题,通常无法将面积问题进行有效转化.本文中以八年级“一次函数面积问题”复习课的教学设计为例,阐述如何通过优化问题结构,以问题驱动课堂,以问题变化提高学生解题的热情,引导学生从多角度和全方位进行思考,形成解题策略,深化解决平面直角坐标系中面积问题常用的方法.

1 问题引入,方法归纳

在平面直角坐标系中,直线l1:y=x+2与y轴相交于点A,l1上点B的纵坐标为5.(文中的变式都使用此条件.)

问题1如图1,连接OB求点B的坐标和△OAB的面积.

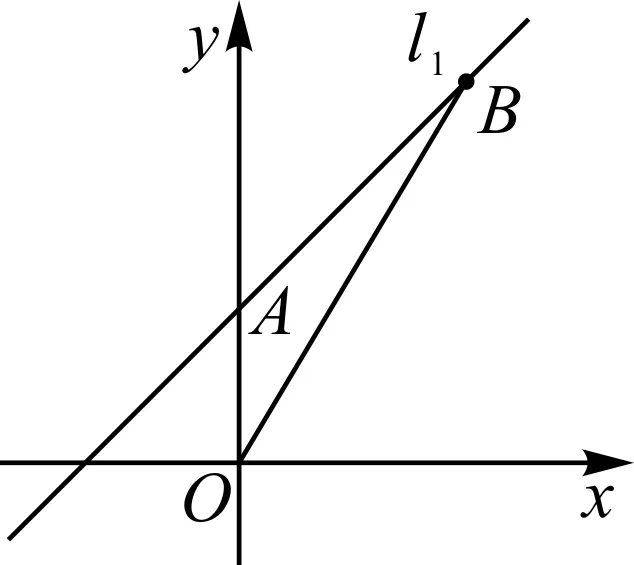
图1

解略.

点评：在平面直角坐标系中,若三角形的一边在坐标轴上或平行于坐标轴(通常称之为“横平竖直三角形”),则可以直接利用三角形面积公式求出其面积.如问题1中△OAB的边OA在y轴上,它是一个“横平竖直三角形”.“横平竖直三角形”是解决一次函数面积问题的突破口.

问题2如图2,若点C(1,0),连接AC和BC,求△ABC的面积.

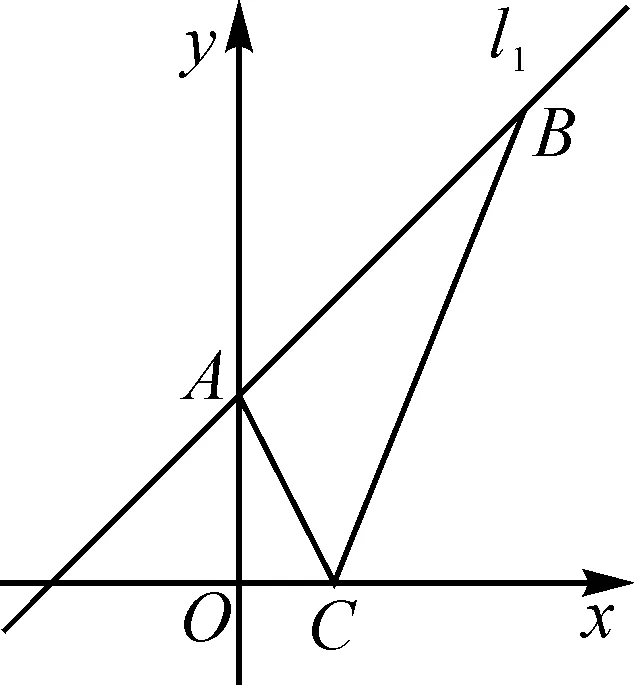
图2

方法1：如图3,过点B分别作x轴和y轴的垂线,垂足分别为F,E,从而把△ABC的面积转化为矩形的面积与三个三角形的面积之差,即

图3

S△ABC=S矩形BFOE-S△AOC-S△BCF-S△EAB.

△ABC的面积由矩形的面积减去三个三角形的面积求得,这种方法称之为“割补法”.

方法2：如图4,过点C作y轴的平行线交AB于点D,则

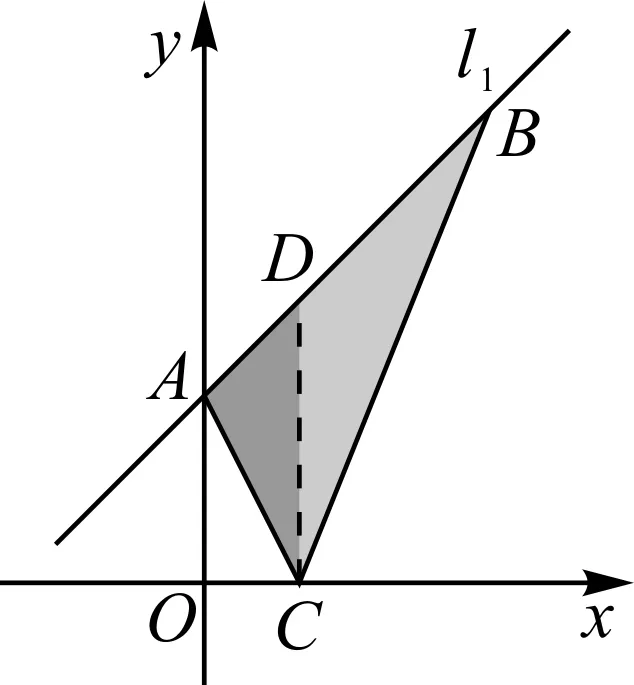
图4

S△ABC=S△ADC+S△BDC

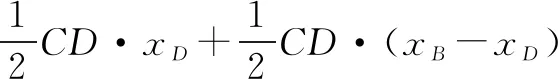
方法3：如图5,过点C作直线AB的平行线交y轴于点E,连接BE.因为△ABC与△ABE同底,且它们的高为两条平行线之间的距离,因此S△ABC=S△ABE,△ABE为前面所说的“横平竖直三角形”.由于AB∥CE,因此直线AB和直线CE的斜率相等,可求出直线CE的解析式,进而求出△ABC的面积.

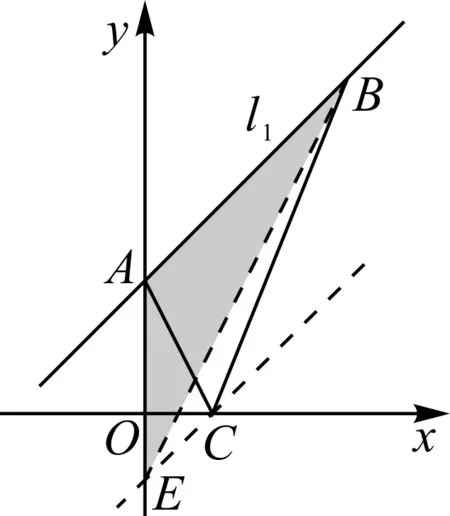
图5

利用“平行线间的距离处处相等”,将△ABC的面积转化为△ABE(“横平竖直三角形”)的面积,此方法称之为“平行面积转化法”.

点评：问题2中的△ABC不是问题1中的“横平竖直三角形”,因此不能通过三角形的面积公式直接求解,需进行转化.问题2的解决引出解决面积问题的三种方法——“割补法”“铅垂法”和“平行面积转化法”,为解决后续复杂的面积问题提供了基本思路和出发点.

2 变式训练,巩固提升

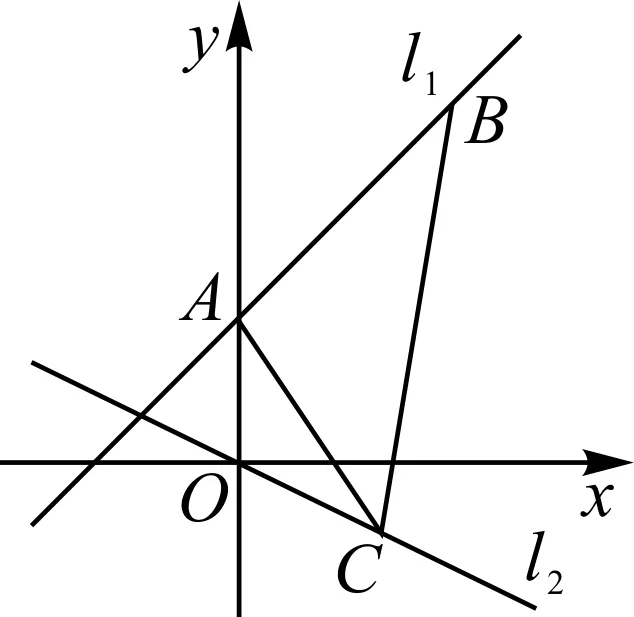
图6

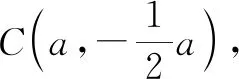
图7

图8

由于AB∥CD,因此kCD=kAB=1,则直线CD的解析式为y=x-3.

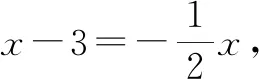
点评：变式1中的点C由“定点”变为直线上的“动点”,题目虽变复杂了,但仍可使用问题2提及的方法来解决,让学生体验方法应用的广泛性.方法1关注“方程思想”,使用“未知数”表示动点C的坐标,利用“铅垂法”表示三角形的面积并利用面积的等量关系构建方程求解;方法2关注“转化思想”,使用“平行线”将△ABC的面积转化为△ABD(“横平竖直三角形”)的面积,将点C看成是两条直线的交点.

变式2如图9,在变式1的条件下,P是线段AB上的动点,若直线CP平分四边形OABC的面积,求点P的坐标.

图9

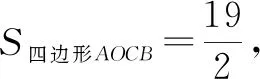
图10

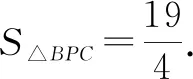
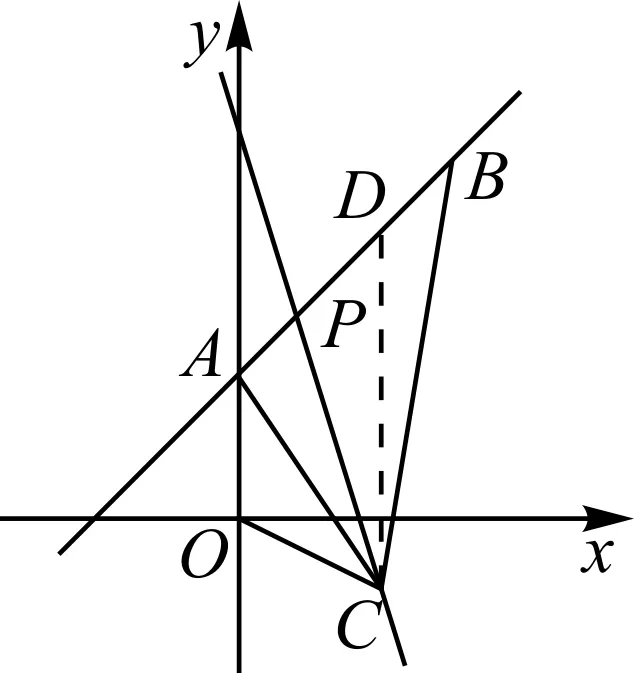
图11

方法3：“平行面积转化法”.如图12,过点O作AC的平行线,交AB于点D.由△ADC与△AOC同底等高,可得S△AOC=S△ADC.则S四边形AOCB=S△ABC+S△AOC=S△ABC+S△ADC=S△BDC.

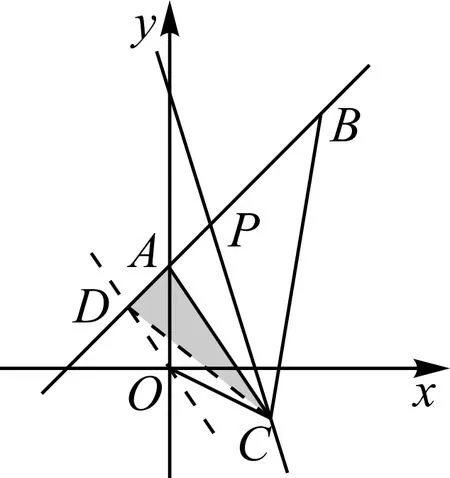
图12

将四边形AOCB的面积则转化为△BDC的面积,又直线CP平分四边形AOCB的面积,可知CP平分△BDC的面积,故P为线段BD的中点.

点评：变式2为动直线平分不规则四边形的面积问题,综合性和难度都有提升,学生通过分析问题情境,运用已有的学习经验将陌生的新问题转化为已知问题,精选方法进行解决.方法1以“分割法”为载体,经由“横平竖直三角形”求解;方法2利用“未知数”表示动点P的坐标,利用面积的等量关系构建方程;方

法3“平行面积转化法”最巧妙,利用平行将四边形AOCB的面积转化为△BDC的面积,符合条件的点P即为线段BD的中点.将不规则图形的面积转化为我们熟悉的三角形面积,由“陌生”到“熟悉”,“一题多解”提高了学生思维的灵活性,拓宽了解题思路,更增加了学习数学的兴趣.

3 反思与小结

3.1 关注问题的设置

复习课常常以问题为导向,解题为驱动.有层次、有梯度、系统化的问题能激发学生的求知欲,引发学生深度思考.在“一次函数面积问题”的变式训练中,笔者利用相同的问题背景,对条件进行重新配置与组合,创设有层次的问题,这些问题虽各不相同,但相互联系.从“问题1”到“变式2”层层递进,由简单的“横平竖直三角形”求面积,到“动点”的面积问题,再到平分不规则四边形的面积问题,由“静”至“动”,从“简单”到“复杂”.学生深入思考,使用多种方法解决问题,体验成就感,不断加深对解题思路和技巧的理解,为后续二次函数面积问题的学习作铺垫.

3.2 关注数学思想的渗透

《义务教育数学课程标准(2022年版)》要求“能够回顾解决问题的思考过程,反思解决问题的方法和结论,形成批判性思维和创新意识”.从“变化的”问题中提炼出“不变的”方法,促进数学思想的内化.“模型思想”:问题1促使学生关注“横平竖直三角形”,后续变式题中的三角形都可通过“分割”或“平行”转化为“横平竖直三角形”来求面积.“方程思想”:利用“未知量”表示动点,利用“等量关系”构建方程,这是解决动点问题的基本思路.“转化思想”:将“普通三角形”的面积转化为“横平竖直三角形”的面积;将“不规则四边形的面积”转化为“三角形的面积”,化“繁”为“简”,化“陌生”为“熟悉”.“转化思想”不仅是有效的思维方式,更在数学的学习过程中扮演着重要的角色.

3.3 关注有针对性的专题训练

“双减”政策对初中课后作业的设计与优化提出了更高的要求.我们要改变当前过量的、低效的、机械的作业训练,提高课后作业质量.笔者认为教师首先要“下题海”,“见识”更多的题目,而仅仅靠做题是不够的,还要对题目进行归纳和整理,将题目的技巧、方法和思路进行总结.课前精选例题,并对例题进行分析、整合、挖掘与拓展,让学生进行有针对性的专题训练,而非盲目地“多做题”;课堂中进行“变式教学”,用问题的多种变式组织课堂架构,将解题方法和数学思想作为贯穿课堂的主线,帮助学生巩固所学知识,提升解题技巧,内化数学思想.Z