Explosive synchronization of multi-layer complex networks based on star connection between layers with delay

Yan-Liang Jin(金彦亮), Qian-Yuan Han(韩钱源), Run-Zhu Guo(郭润珠),Yuan Gao(高塬), and Li-Quan Shen(沈礼权)

1Key Laboratory of Specialty Fiber Optics and Optical Access Networks,Joint International Research Laboratory of Specialty Fiber Optics and Advanced Communication,Shanghai Institute for Advanced Communication and Data Science,Shanghai University,Shanghai 200072,China

2School of Communication and Information Engineering(SCIE),Shanghai University(SHU),Shanghai 200000,China

Keywords: multi-layer networks,Kuramoto model,explosive synchronization,delay

1.Introduction

The origin of complex networks can be traced back to the Swiss mathematician Euler’s “Seven Bridges” problem.Because of the common topological statistical properties of networks in reality,the small-world network characteristics[1]proposed in 1998 and the scale-free network characteristics[2]proposed in 1999 have made complex networks a hot research topic.They have become the focus of many disciplines such as graph theory, computer science, biological science, economics, sociology, and nonlinear dynamics.[3-6]In complex networks, the interaction between nodes results in nonlinear synchronization, such as the flash of fireflies, the chirp of crickets, the applause of music venues, and the synchronous discharge of brain nerves,etc.[7-9]Meanwhile,some engineering applications have synchronous behavior:the dumbbell network of Wuhan University,[28]the power grid and information network,and so on.

The underlying mechanism behind nonlinear synchronization has become the focus of complex dynamics.The initial research based on the coupled Kuramoto[10,11]phase oscillator and the synchronization of the coupled chaotic oscillator shows that in most cases, the order parameter characterizing the macroscopic cooperative motion of the system continuously increases after passing through the phase transition point when the system changes from a noncooperative state to a cooperative state.[12]However, most existing research over the past decades only considered second-order phase transition synchronization on single-layer and doublelayer networks.[12-15]The first-order phase transition of complex networks has not yet been discovered.After the discovery of explosive seepage in random networks and scale-free networks,[16,17]the first-order phase transition(explosive synchronization,ES)in complex networks was found and has attracted extensive attention.The early ES required highly heterogeneous network topology, which greatly limited research of ES theory.Because of this heterogeneity, researchers proposed the Kuramoto model based on frequency weight,[18]which makes ES independent of special topological structure,and it was then widely used for ES of single-layer complex networks.Huet al.also provided an accurate solution for the ES phase transition point of a single-layer network.[19]In addition,Wuet al.studied the effect of the single-layer network with delay on ES.[20,21]In the initial stages, ES was mainly considered a single-layer network;ES on multi-layer networks was in its infancy.

Thereafter,research on ES has extended from single-layer to multi-layer.[22-25]Liuet al.simulated the framework of mutual co-evolution of networks[23], but the synchronization between network layers was not explained.Shuet al.discussed the synchronization optimization problem of a multilayer network structure composed of a star structure chain.[24]However, the adopted inter-layer connection mode was only connected through the hub node of the star network, and did not fully consider the impact of other leaf nodes on the interlayer synchronization of the network.Jalanet al.concluded in a study of multi-layer networks that adjusting the network properties of one layer can change the dynamic characteristics of other layer networks.[25]The influence of ES between layers was also verified, but the exact phase transition point was not given.Yaoet al.studied the Kuramoto model on a double-layer network,[26]providing the exact solution of the backward phase transition point of ES but the multi-layer network and the connection mode between layers were not discussed.Guoet al.extended it to multi-layer networks based on Yao,[27]summarizing the Kuramoto model on multi-layer networks,and taking the star connection model as the research object.This model discusses the interaction between networks in the ideal state,but it lacks consideration of the delay in the real network interaction, That is, the influence between the non-delay layer and the delay layer.

Considering the disturbance in a real network, there is a delay in the information exchange between the networks.In the ES of complex networks,the synchronization between actual networks is not as ideal as the theory,there is a delay effect.To understand the stability of ES of multi-layer complex networks more deeply and realize control of synchronization,it is of practical and academic significance to study the ES of multi-layer networks with delay.For example, it is of importance to synchronization generation and control of multilayer complex systems with a time delay in real life, such as in the synchronization of double-layer dumbbell networks.[28]This paper develops a delay parameter based on this model,and a coupling model with delay is derived which gives the backward phase transition point theoretically.Additionally,we study the influence of parameters on multi-layer ES with delay.

The main contributions of this paper are as follows: (i)The delay parameter is introduced into the multi-layer network coupling synchronization, and a multi-layer star ES model with delay is deduced.The influence of delay on ES is also explored.(ii) Numerical results reveal the influence of different parameters on ES with delay, including average node degree,inter-layer coupling strength,and network topology.

The structure of the rest of this paper is organized as follows: Section 2 introduces the Kuramoto model of a multilayer network with delay and analyzes the average field theory of the model.Section 3 introduces the experimental results of ES with different parameters using this model.Section 4 gives the conclusion.

2.Model

2.1.Kuramoto model of a multilayer network

Compared with the Kuramoto model of a single-layer network, the Kuramoto model of a multi-layer network is relatively more complex.The topological structure of the multilayer star network is shown in Fig.1.

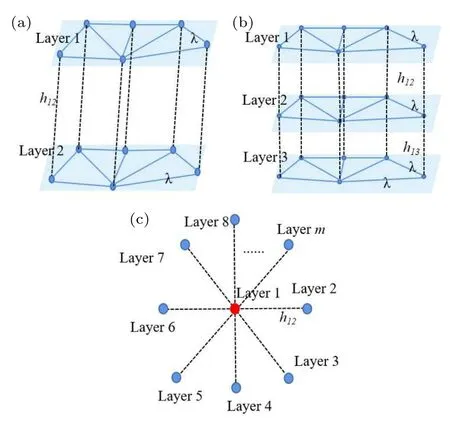
Fig.1.Topological structure of multi-layer star network. λ represents the coupling strength in the layer(blue solid line),and hi j represents the coupling strength between layer i-th and layer j-th (black dotted line).(a) 2-layer network.(b) 3-layer network.(c) m-layer network.The red dot represents the center layer,and the blue dots represent the leaf layer.

The ES of multi-layer complex networks needs to be divided into the central layer and the leaf layer by the coupling strength.The central layer acts on all leaf layers,such as layer 1 in Fig.1.Assuming that each layer of the network containsNcoupled oscillators, Guoet al.[27]gave the Kuramoto formula of the multi-layer star network:

Equation (1) is the equation of the center layer model, and equation (2) is the leaf layer model, wherei=1,...,Nanda=2,...,m,irepresents thei-th oscillator in the center layer,andarepresents thea-th layer of the leaf layer.〈k〉represents the average node degree of each network layer.λirepresents the intra-layer coupling strength of thea-th layer,h1arepresents the coupling strength between the central layer and thea-th layer,θiandθjstand for the phase of thei-th andj-th oscillators of the central layer, respectively,θ＇jrepresents the phase of the node connected to the nodeion the network of another layer,andωirepresents the absolute value of the natural frequency of thei-th node.Aijrepresents the adjacency matrixMbetween multi-layer star networks,where the elements are

whereAirepresents the adjacency matrix of the star network of each layer,I,0 represent the identity matrix and the zero matrices, respectively, and represent whether the layers are connected.

Based on the coupling dynamic behavior formula between multi-layer star networks,the Kuramoto model of multilayer star networks is designed.Because the multi-layer star network is composed of the center layer and the leaf layer,the design is divided into two parts:

(i)Central layer with delay When the delay layer is the central layer,as shown in Fig.2,all networks in the leaf layer will be directly affected by the delay.The purpose is to study the synchronization of each layer of the network.

Fig.2.Central layer with delay.

At this,thedynamic formula is

Equation (4) is the Kuramoto model of the central layer and equation(5)is the Kuramoto model of the leaf layer.

(ii) Leaf layer with delay When the leaf layer with delay,the central layer connected to it is directly affected by the delay layer,while all the remaining leaf layers are not directly affected by the delay layer, but are indirectly affected by the delay layer, as shown in Fig.3.The purpose is to study the synchronization of each layer of the network when the delay layer directly acts on one layer of the network or indirectly acts on other network layers.

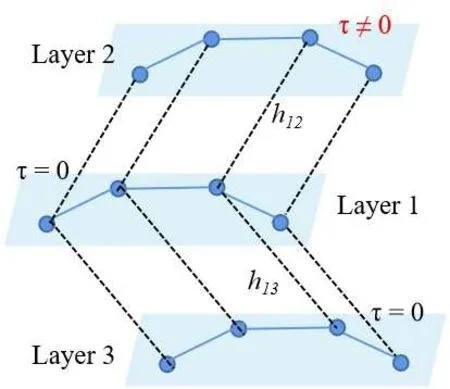
Fig.3.Leaf layer with delay.

Compared with the first one, the leaf layer at this needs to be divided into a delay layer and a non-delay layer, so the dynamic formula is

Equation(6)is the Kuramoto model of the central layer,equation (7) is the Kuramoto model of the leaf layer with a delay layer,and the Kuramoto model of the leaf layer without delay is the same as Eq.(4).

2.2.Theoretical analysis

To facilitate the research,this paper uses the same topology and natural frequency of the nonfully connected star network to form a multi-layer network model.Based on the case that delay is introduced into different layers, it is necessary to analyze the dynamic evolution of Kuramoto oscillators with delay introduced into the center layer and the leaf layer respectively.

2.2.1.Backward phase transition with delay in the central layer

When the average node degree is large enough, ignoring the fluctuation under the thermodynamic limit conditions,taking the Kuramoto model, equation(4), of the central layer as an example,equation(4)can be rewritten as

whereP(k＇) denotes the degree distribution function andρ(k＇;θ＇,t) denotes the probability density function of the oscillator with nodeKand phase at timet.Based on the definition of order parameter,[29]represents the phase of thei-th node with delay, andrepresents the phase corresponding to thei-th node in the leaf layer network.The formula of the corresponding order parameter is defined as

whereψrepresents the average phase of the network,R ⊆[0,1].WhenR=0,this means non-complete homomorphism;whenR=1,this denotes complete homomorphism,i.e.,complete synchronization.

Based on the mean-field theory and the self-consistent theory,[30,31]equation(9)is brought into Eq.(8),and then the mean-field form is obtained as

By defining the phase difference between the instantaneous phase of the network oscillator and the average phase of the system as Δθ=θ-ψ,equation(10)may be rewritten as

When the system tends to the synchronous state,the system is in the synchronous phase-locked state ˙θ(t)=0, and-θi(t)≈0,from which the phase at phase locking can be obtained:

It can be seen from Eq.(12) that Δ ˙θiwith coupling strengthλthe increase will gradually approach zero, the order parameter equation can be written as follows:

where Δθ+and Δθ-represent synchronous states when the natural frequencies are positive and negative, respectively.If Eq.(12)is brought into Eq.(13),the following is obtained:

The linear stability analysis of the homomorphism shows that when Eq.(14)has a non-zero solutionλ,the value range is as follows:

From this, it can be concluded that the critical coupling strength of the backward phase transition of the central layer network is expressed as

Similarly,the expression of the critical coupling strength value of the backward phase transition of the leaf layer network when the central layer contains delay can be deduced by Eq.(5)as

2.3.Backward phase transition with delay in the leaf layer

The formula derivation process of the backward phase transition point with delay in the leaf layer is similar to the process of delay in the central layer, so we will not repeat it here,and the results will be directly given by

The Kuramoto model,equation(6),of the central layer allows deduction of the critical coupling strength of the backward phase transition to be given by Eq.(18).The critical coupling strength of the backward phase transition derived from Kuramoto Eq.(7)with delay and Kuramoto Eq.(4)without delay in the leaf layer is the same,which is Eq.(19).

From the above formulas, it is found that the delay does not affect the critical coupling of the backward phase transition of explosion synchronization.From Eqs.(14)-(19),it can be seen that the inter-layer coupling strengthhand the average node degree〈k〉are the direct factors affecting ES.Increasing the coupling strength between layers will increase the backward critical coupling strength and hinder the backward phase transition;conversely,increasing the average node degree will reduce the backward critical coupling strength and promote the backward phase transition.In addition,there are other indirect factors,such as the number of network layersmand the number of network nodesN.The network topology does not affect synchronization.To verify the theoretical analysis results,this paper will introduce the delay into the network layer and conduct numerical simulations and experimental analyses.

3.Experimental analysis

In this section, the ES of multi-layer complex networks with delay layers will be simulated in detail.In the experiment, based on the previous theoretical analysis, the effects of delay,average node degree,network layers,network nodes,and network topology on ES are studied after introducing a delay.During the numerical simulation, the parameters and parameter values are shown in Table 1.

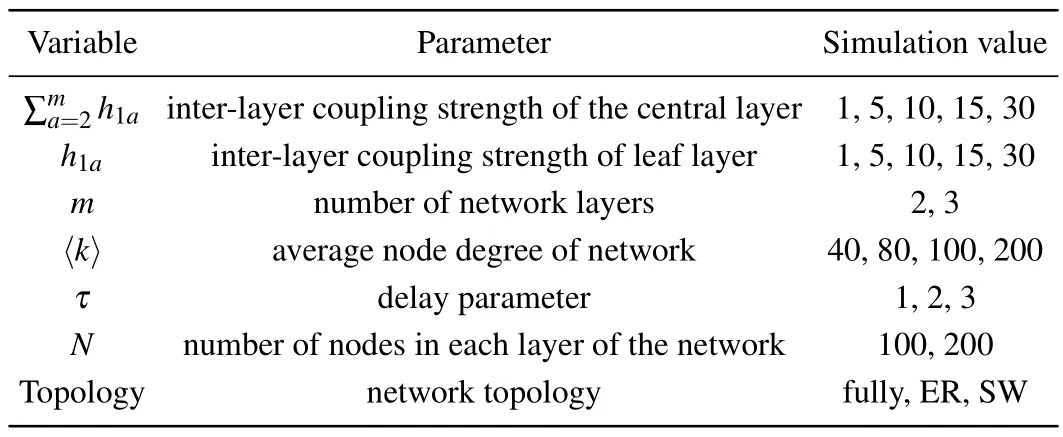
Table 1.Simulation parameters.

3.1.Simulation of structural parameter change

3.1.1.The influence of inter-layer coupling strength on ES

In this section,a double-layer fully connected network is selected,withN=200 for each layer.The first layer is set as the delay layer, where delayτ=1 and the coupling strength between layers ish=h12=1,5,15,and 30.The influence of coupling strength change between delay layers on the ES will be discussed below.

Fig.4.Synchronous phase transition of the order parameter is changed with delay.(a) h = h12 = 1.(b) h = h12 = 5.(c) h = h12 = 15.(d)h=h12=30.

In Fig.4,R1F and R1B curves respectively represent the forward phase transition and backward phase transition curves of the central layer, and R2F and R2B respectively represent the forward phase transition and frontback phase transition curves of the leaf layer.It can be seen from Fig.4.that the backward phase transition points of the center layer and the leaf layer increases with the increase of the interlayer coupling strength when the delay is determined, which is in line with the theoretical results.The forward phase transition point decreases with the increase of interlayer coupling strength.It is concluded that with delay,the interlayer coupling strength promotes the forward phase transition and hinders the backward phase transition.

3.1.2.The influence of average node degree and network node number on ES

In this section, the Erd¨os R´enyi random network(ER)is used with the number of nodesN=100, 200, and the average degree of nodes〈k〉=40,80.The first layer is set as the delay layer, where the delayτ=1, the coupling strength between layersh=h12=10, and the frequency distribution is the Lorentz distribution.Next, we will discuss the impact of the average node degree and node parameters of the network on ES with delay.

In Fig.5, (a)-(b) and (c)-(d) have the same number of nodes and different average node degrees.It can be seen from the figure that the backward phase transition point in (a) is larger than the phase transition point in(b),and has no effect on the forward phase transition point.The same conclusion is reached for(c)and(d).Panels(a)and(c),and(b)and(d),have the same average node degree and different node numbers.From the figure,it is found that the backward phase transition of(a)and(c)is the same,and the same conclusion can be obtained for(b)and(d).It can be concluded that when the delay and inter-layer coupling strength are the same, the average node degree of the network hinders the backward phase transition of explosive synchronization of the network,and has no effect on the forward phase transition point;the number of nodes in the network has no direct influence on the phase transition point of ES,which conforms to the theoretical derivation in Eqs.(16)and(17).

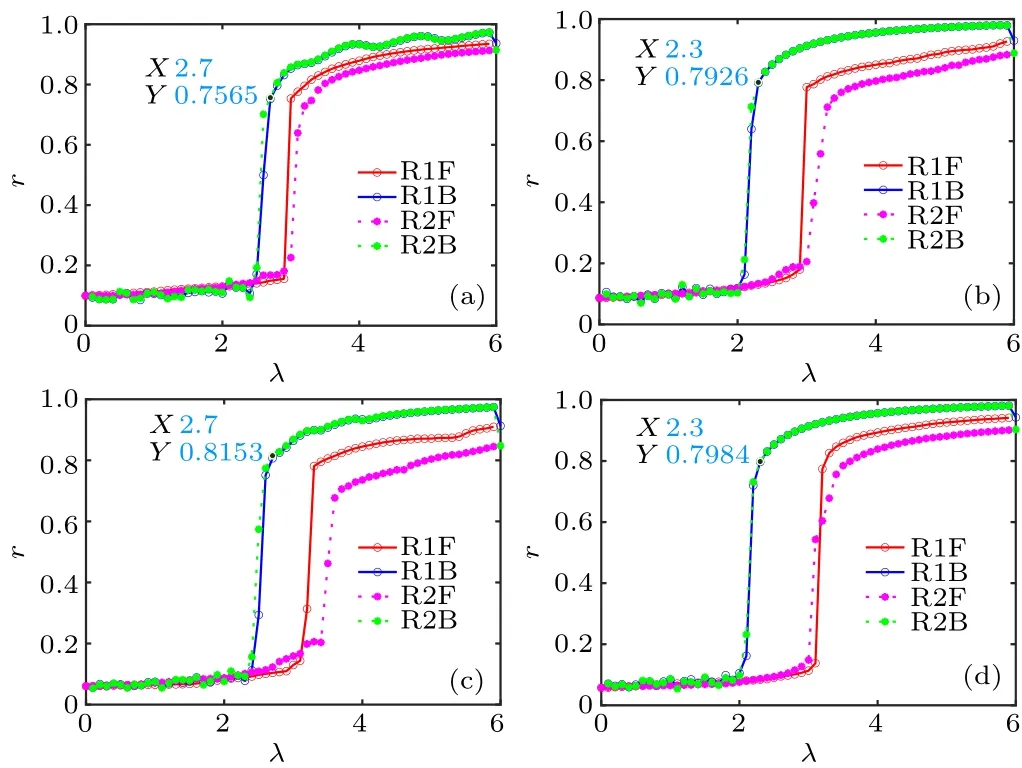
Fig.5.Synchronous phase transition diagram at different average node degrees.(a) N =100, 〈k〉=40.(b) N =100, 〈k〉=80.(c) N =200,〈k〉=40.(d)N=200,〈k〉=80.

3.1.3.The influence of network topology on ES

This section selects three network topologies: smallworld network (SW), fully connected network, and ER to study the impact of different topologies on ES with the same delay and layer coupling strength.The first layer is set as the delay layer, where the delayτ=1, the coupling strength between layersh=h12=10,and the frequency distribution is the Lorentz distribution.The results of the simulations are shown in the following figure.

In Fig.6, when the delay and the inter-layer coupling strength are the same, and the network topology is different,although the change of the order parameter is different in the phase transition process,the phase transition point remains unchanged,that is,the network topology has no direct impact on the ES.

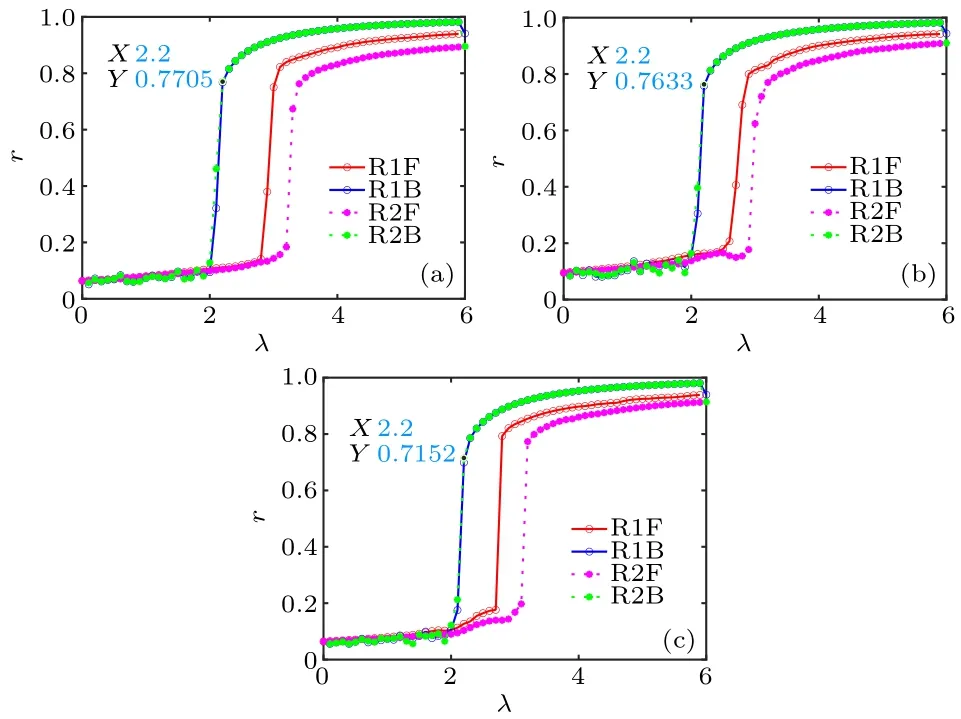
Fig.6.Synchronous phase transition diagrams under different topologies.(a)Small-world network(SW):N=200,〈k〉=100.(b)Fully connected network (fully): N =100, 〈k〉=100.(c) Erd¨os R´enyi random network(ER):N=200,〈k〉=100.

3.2.Simulation of delay parameter change

In the simulation experiment of structural parameters, it is concluded that the average node degree of the network and the coupling strength between layers are the direct factors that affect the ES of multi-layer complex networks.Next,we will discuss the influence of delay factors on ES.

3.2.1.Synchronous simulation with delay in the central layer

This section uses a double-layer fully connected network as the research object.The first layer is set as the central layer and the other layer as the leaf layer.The number of nodes in each layer of the network isN=200, the coupling strength between the layers ish12=10,and the effect of different delay values on the ES of the central layer and the leaf layer is explored.

In Fig.7, the results of the backward phase transition point in (a)-(c) are the same through different delay parameters of the central layer.The instantaneous delay value does not change the backward phase transition point of ES, which is consistent with the backward phase transition point formula derived in the paper.For the forward phase transition point,it will change the forward phase transition point of the central layer and the leaf layer, and also affect the order parameter value of the forward phase transition of the direct-acting leaf layer.

Fig.7.Phase transition diagram under different delay parameters(m=2).(a)τ =1.(b)τ =2.(c)τ =3.

3.2.2.Synchronous simulation with delay in the leaf layer

This section takes the three-layer fully connected network as the research object.The first layer is set as the leaf layer,the second layer as the center layer,and the third layer as the other leaf layer.The number of nodes in each layer of the network isN=200,and the coupling strength between layers ish12=10.We explore the impact of the introduction time delay of the leaf layer on the ES of the center layer and other leaf layers.

In Fig.8,by introducing a delay in the leaf layer,we get the same conclusion as for two layers.That is, the change of delay parameter will not affect the backward critical coupling strength,but will change the forward critical coupling value of the interacting network, and affect the order parameter value of the directly interacting network.

Fig.8.Phase transition diagram with different delay parameters(m=3).(a)τ =1.(b)τ =2.(c)τ =3.

4.Conclusion

In this paper, we study ES under a frequency-weighted,coupled Kuramoto model for multi-layer networks with interlayer star network connections with delay.This paper mainly focuses on the influence of parameters on the backward critical coupling strength after the introduction of delay.Through theoretical and experimental data analysis using this model, the coupling strength between layers and the average node degree of the network has a direct impact on the backward critical coupling strength of ES.Increasing the coupling strength between layers will hinder the backward phase transition,and increasing the average node degree of the network will promote the backward phase transition.Then we explore the impact of other parameters on ES in multi-layer networks and find that the number of network layers, nodes, delay parameters, and network topology make no difference in the backward phase transition of the network, but the delay parameters have an impact on the forward phase transition.The critical coupling value of the backward phase transition is obtained by a meanfield analysis,which proves the correctness of the experimental results.

To ensure the security of synchronization, Liuet al.[32]studied the synchronization encryption scheme of two-layer complex dynamic networks, and then optimized the synchronization of multi-layer networks based on the graph comparison method.[33]Liet al.[34]made more economic and more research on the synchronization control of multi-layer complex networks.This is of great significance to the generation and control of multi-layer complex systems with time delays in real life.The model proposed in this paper has a one-to-one correspondence between nodes in the network layer.In real life, a node may act as multiple nodes of the network in another layer at the same time.Therefore, in the future it will be worth studying the synchronization phenomenon of one-tomany connected multilayer networks.