Optimal Kalman-like filter for a class of nonlinear stochastic systems

Shulan Kong ,Yawen Sun ,Huanshui Zhang

a School of Mathematics Science, Qufu Normal University, Qufu, China

b College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao, China

Keywords:Kalman-like filter Multivariate analysis Auto-correlated and cross-correlated stochastic parameters Uncorrelated pseudo-noises

ABSTRACT This paper deals with an optimal Kalman-like filter for nonlinear discrete-time systems aided with auto and cross-correlated noises and stochastic parameter matrices involved in state and measurement equations,and random nonlinearity.The random variables are proposed by their statistical characteristics while the inquiry is focused on stochastic multivariate analysis and calculation.For the nonlinear system with the auto and cross-correlated noises and stochastic parameter matrices,an equivalent system is first reconstructed by decomposing stochastic parameter matrices and introducing uncorrelated pseudonoises.Then a recursive filter that ensures unbiasedness and minimizes the error variance is designed for the newly transformed equivalent system.Finally,the filter is verified by applying it to some numerical simulations.

1.Introduction

With wide applications in engineering field,such as robot positioning and digital control of chemical process,the Kalman filter has attracted extensive attention;see [1-3].In addition,the Kalman filter is closely related to ocean modeling and parameter estimation.For example,an extended Kalman filter was proposed for a multilayer nonlinear quasi-geostrophic ocean circulation model [4].Kalman filter techniques were used to forecast near-surface ocean winds [5],and a Kalman Bucy filter was implemented for data assimilation with an ocean model [6].In recent years,the Kalman filter with a running-in-place algorithm was applied to an ocean circulation model [7],a coastal ocean model [8],while an ensemble Kalman filter was used to evaluate the effects of the general ocean circulation model [9].The Kalman filter has a very wide range of applications in ocean engineering,which suggest it is a practical platform for designing additional filters.

The problem of filtering has received continuous attention since it was proposed,see e.g.Kalman filter [10-13],H∞filter [14] -[15],generalized Kalman filter [16]-[18],orL∞-induced filter [19].Responses to this problem,have included a newly developed and robust Kalman filter for detecting and bounding the influence of outliers as proposed for discrete linear systems generated by thicktailed noise distributions [12] ;an adaptive Kalman filter that uses linear systems known parameter matrices for target tracking in underwater acoustic sensor networks [13] ;and a novel method of cubature Kalman filter based on Quasi-Newton proposed for an inertial navigation nonlinear system provided with magnetic sensors[17].

In many situations,the parameter matrices of systems are randomly disturbed by outside condition describing random phenomena,such as parameter uncertainty,Markov jump,multiplication noise and packet loss.However,the structure of parameter uncertainties is usually too complicated in real-world situations and thereby problematic to effectively replicate.Addressing this question,parameter uncertainties of the systems have been developed by using statistical information instead of structural information recently.In particular,designing an appropriate filter is of particular interest for discrete-time systems with known statistical information of stochastic parameter matrices.For this kind of the linear systems with known statistical information of stochastic parameter matrices,an optimal state estimator was pioneered by changing the system into one that used deterministic parameters and statedependent additive noises,which were statistically independent to time [20].The least-squares quadratic filter and robust optimal filter for the systems including independent stochastic parameter matrices,process noise and measurement noise have been respectively addressed;see [21] and [22].A dual-state filter has been designed for a relative velocity aiding strapdown inertial navigation system [23].Based on [20],an optimal filter for systems owning cross-correlated noises and random parameter matrics has been designed by constructing a de-correlation framework and using the results of Kalman filter [24].A recursive distributed Kalman-like optimal linear unbiased fusion filter which minimizes the error variance has been proposed for multi-sensor systems owning correlated noises and stochastic parameter matrices [25].

It is worth noting that few results are reported on the filter of the discrete nonlinear systems with parameter uncertainty [26-30].A recursive filter is discussed for nonlinear systems with correlated noises,random parameter matrices,and measurements [26].An optimal approximating nonlinear filter is considered from stochastically convergent state process approximations [27].The one-step prediction is obtained by solving a deterministic optimization of time varying systems which have unknown inputs and correlated noises [29].An improved Kalman filter with maximum correntropy cubature is given to deal with the measurement outliers in cooperative localization of autonomous underwater vehicles [30].Unfortunately,the existing work [17] and [26-30] does not simultaneously concern the nonlinear systems with noises and crosscorrelated stochastic parameter matrices.There is little literature,that examines using filter matrices of correlated stochastic parameters and noises,for nonlinear discrete-time systems.We want to address this research deficit by designing filters of the nonlinear discrete-time systems that have correlated and cross-correlated noises and stochastic parameter matrices.

Motivated by the studies described above,we are going to design a distributed Kalman-like filter for discrete-time nonlinear systems.The filter will be constructed from auto-correlation and cross-correlation stochastic parameter matrices,include noises of the state and measurement equations,and random nonlinearity.It is differentiated from the previous work,as we will first establish the optimal filter problem of nonlinear systems with both autocorrelation and cross-correlation coefficient matrices and noises.Two points below will highlight the contributions of the paper: (1)A de-correlation framework is established to decompose correlated noises and parameter matrices;(2) The developed recursive filter is applicable for online implementation.

The rest of the paper is arranged.The problem is proposed in Section 2.An optimal filter is designed in Section 3.The effectiveness of our obtained filter is shown by simulating a example in Section 4.Section 5 gives conclusions.

Notations.The symbolsRnandRm×nare denotedn-dimensional Euclidean space andm×nmatrice vector space.The operationE[·]is denoted as the mathematical expectation of random variable.Let denoteA=(Aij)m×nandE[A]=(Eaij)m×nfor a random parameter matrixA∈Rm×nand the expectation ofA.For a deterministic matrixB,BTandB-1denote its transpose and inverse,its trace is written astr(B).0m×nandInarem×nzero matrix andn×nidentity matrix.δijstands for the Kronecker’s delta function.For two stochastic vectorsxandy,their covariance matrix isCo(x,y).

2.Problem formulation

The discrete-time system is considered as below

where a time indexkis given,the state vectorxk∈Rnis to be estimated,the outputyk∈Rqis measured,Ak∈Rn×n,Dk∈Rq×n,Bk∈Rn×mandGk∈Rq×qare stochastic parameter matrices with known mean matrices,which are independent of the statexk.The noisesvk∈Rmandwk∈Rqare zero mean.The nonlinear functiong(xk,ξk) represents the stochastic nonlinearity.The Gaussian noiseξkis zero mean.It is uncorrelated with other noises and independent ofAk,Dk,Bk,Gkandxk.x0is the initial value of state which is independent of other random variances and has known meanμ0and covarianceW0.

For (1),the following assumptions are also made.

(A1)The sequencesvkandwkhave known covariances and cross-covariances

Co(vk,vj)=Rkδkj,

Co(wk,wj)=Qkδkj,

Co(vk,wj)=Skδkj.

They are independent of the matricesAk,Dk,BkandGk.

(A2)The matricesAk,Dk,Bk,andGkare only correlated at the same time instant,and the covariances of the entries of them are known.

(A3)The functiong(xk,ξk) withg(0,ξk)=0 has the following statistical information:

wheretis a known nonnegative integer,ГiandΠi(i=1,2,···,t)are known matrices.

The aim of the paper is to design an optimal Kalman-like filterat time instantkbased on observationYk={y1,y2,···,yk}.It is to find the appropriate filter gain matrix,based on the processYk,that minimizes the filter error covariance matrix.

3.Optimal kalman-like filter of the system

Here system (1) is redescribed as a new one by constructing uncorrelated noises as the same approach in [24].Then the optimal Kalman-like filter is designed.

3.1.Problem transformation

We shall separate a stochastic matrix into random and deterministic parts.The matricesAk,Dk,BkandGkcan be rewritten as follows:

Lemma 1[24].If the stochastic vectorxand parameter matrixAare independent,then

Theorem 1.System (1) is equivalently changed into the one as follows

where

MkandNkare called the uncorrelated pseudo-noises withE[Mk]=0n×1,E[Nk]=0q×1and respectively covariance matrices

Proof.Assume thatLk∈Rn×qis a weight matrix.Let add one termLk(yk-Dkxk+Gkwk) to the first equation of the system (1),the equation becomes

Then (1) can be changed into the following form

Under Assumption (A1) and the condition thatAkandDkare independent of the statexk,we have

then we have

Therefore it is obtained that

Remark 1.An equivalent system (2) is reconstructed by decomposing stochastic parameter matrices and acquiring uncorrelated pseudo-noises.The new system has deterministic coefficient parameters.The additive noisesMkandNkare dependent on state and some stochastic matrices,but they are uncorrelated pseudonoises with deterministic statistical information.Theorem 1 offers convenience for designing the Kalman-like filter of this kind of the nonlinear stochastic systems.

3.2.Optimal kalman-like filter design

For the system (2),a recursive filter is adopted as follows:

Before obtaining our main results,we first deal with the unbiasedness of the filter as well as the recursion of the second-order moment for state and prediction error covariances.We shall derive the following conclusions.

Theorem 2.Consider the system (2) with initial value,then the proposed filter (3) can achieve unbiased estimation.

Proof.The proof is processed by mathematical induction.

FromTheorem 1and the statistical properties of the nonlinear functiong(xk,ξk),it follows that

Theorem 3.For the system (2),the second-order momentXkof the statexk+1satisfies that

Proof.According to the properties of random variables ofvkandξkas well aswk,it is obtained immediately that

Considering the property of the conditional expectation,it follows from the assumption (A3) that

Hence

Theorem 4.Consider the system (2),the second-order momentWk+1|kof the erroris calculated by

Proof.Consider the error

together with the following equations

Then the second-order moment is reached by

Therefore

Next,the main results are proposed as follows.

Theorem 5.Consider the system (2),the gain matrixFk+1of filter (3) that minimizes the second-order momentWk+1|k+1is given as follows:

Moreover,the minimal error variance of filter is reached as

withW0|0=W0.

Proof.Applying (2),we get

Then focus on the above term,performing a completion of squares,we obtain

where

Now we need to solve the matrixFk+1that minimizes the covarianceWk+1|k+1.ThenFk+1should be chosen as

And the minimalWk+1|k+1is described as

whereW0|0=W0.

Finally we may conclude the following theorem based on Theorem 1 and Theorem 3–5.

Theorem 6.For the system (1),the optimal Kalman-like filter can be recursively calculated by

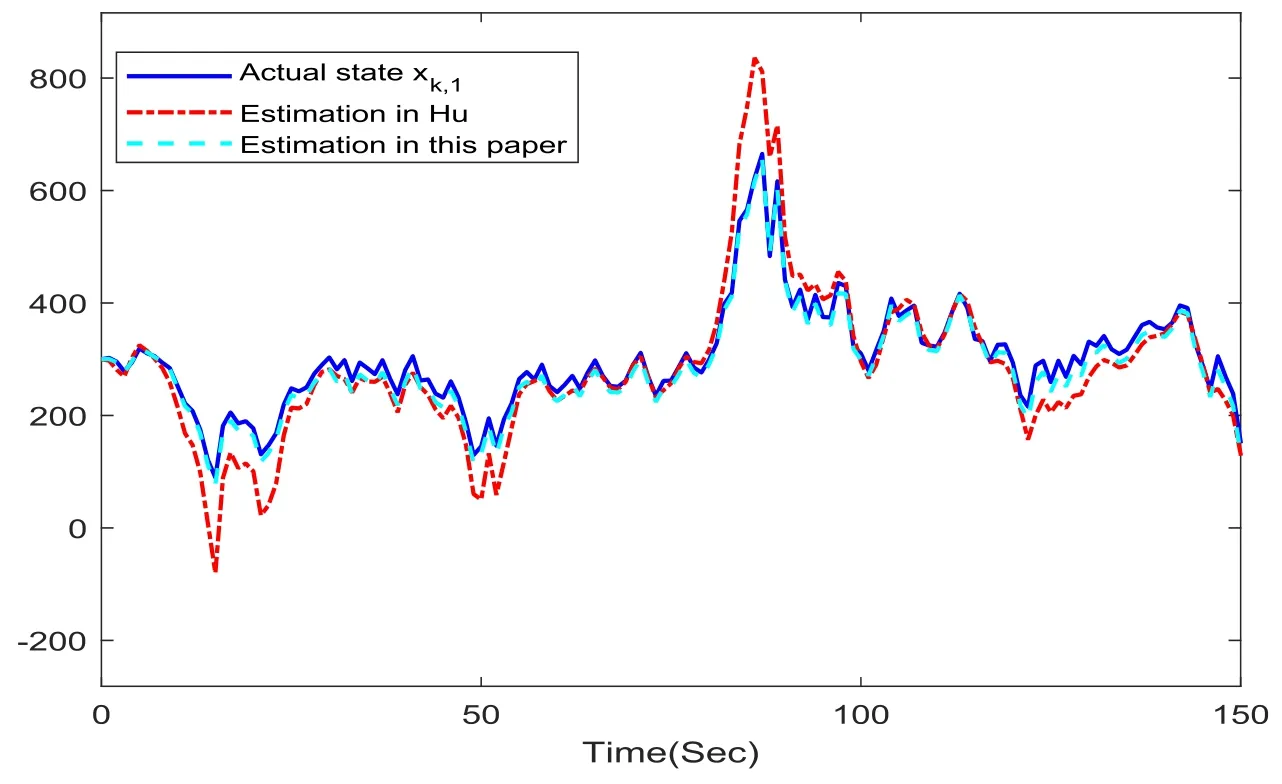
Fig.1. Actual state xk,1 and its estimations.

Fig.2. Actual state xk,2 and its estimations.

Fig.3. Actual state xk,3 and its estimations.

Fig.4. Mean-square error of xk,1.

Fig.5. Mean-square error of xk,2.

with the initial values

Proof.The proof can be directly completed by the above theorems.

Remark 2.The optimal Kalman-like filter for system (1) is designed by introducing a weight matrix and establishing Theorems 1–5.Then a real-time filter method is proposed for the systems owning cross-correlated noises and random parameter matrices.

Remark 3.Our designed filter closely approximates the actual state.It is observed from (3) that the filter is constructed by considering the matrixLkwhich includes the information of all stochastic variables except forvk.The technique used in Theorem 1 is a way out of the dilemma of solving cross-correlated noises and random parameter matrices.Based on lots of literature we have found the technique is uniquely applied for the nonlinear systems.

4.Numerical example

To explain the effectiveness of the designed filter strategy,one example is considered,and numerical simulations are performed by one example below.

Letxk=(xk,1xk,2xk,3)Tandξk=(ξk,1ξk,2ξk,3)Tbe the state and the noise,vk=wkbe Gaussian white noises with mean 0 and variance 0.05,and=μ0=[300 40 9]TandW0|0=0.1I3,consider the nonlinear system (1) with the following parameters:

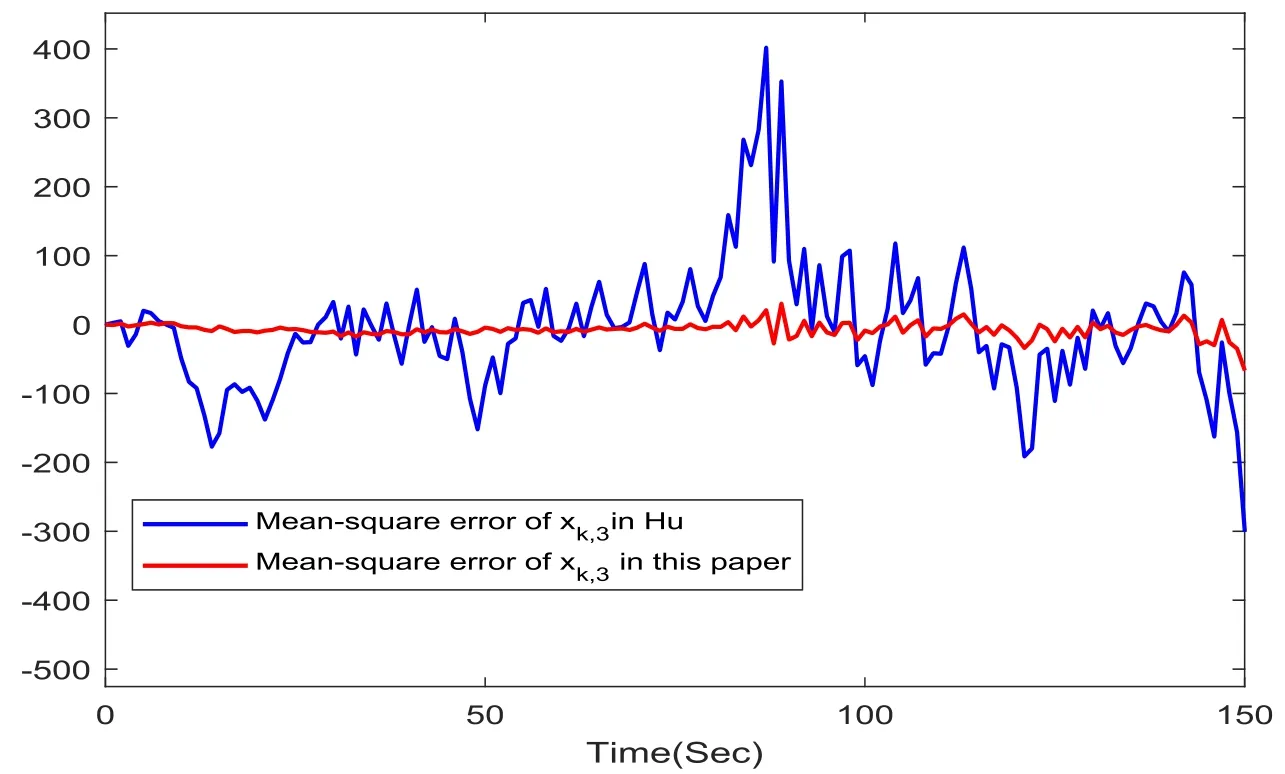
Fig.6. Mean-square error of xk,3.

whereωkand∊kare Gaussian white noises with mean 0,variances 0.2 and 1.The nonlinear function

Fori=1,2,3,di=sign(xk,i) xk,iξk,iwhereξk,idenote uncorrelated noises with mean 0 and covariances 1.It satisfies

The simulations are performed.Figs.1,2,3 show the evolution of the actual state and the filters.The filter curves are compared.It is obvious that our designed filter is closer to the actual state than that in [26] (Hu).More specifically,the filter achieves higher accuracy than that one when the actual state sharply changes.The mean-square error curves of the state estimation are compared in Figs.4,5,6.It can be found that the amplitude of the mean-square error of our filter is smaller than that one for the filter in [26] (Hu).After comparing with each other,we will reach the conclusion that our filter has better performances.This is why we shall use the technique of Theorem 1 to deal with the nonlinear system that owns correlated noises and random parameter matrices simultaneously.

5.Conclusions

We propose a filter scheme for the discrete-time nonlinear system with auto and cross-correlation noises and random parameter matrices involved in the measurement and state,and random nonlinearity.An equivalent system is first reconstructed by decomposing stochastic parameter matrices and introducing uncorrelated pseudo-noises.This allows us to develop a recursive filter that ensures unbiasedness and minimizes error variance for the new equivalent transformed nonlinear system.Finally,the performance of the designed filter is shown by an example.

Declaration of Competing Interest

We certify that this manuscript is original and has not been published,and will not be submitted elsewhere for publication while being considered by ’Journal of Ocean Engineering and Science’.And the study is not split up into several parts to increase the quantity of submissions and submitted to various journals or to one journal over time.No data have been fabricated or manipulated to support our conclusions.The submission has been received explicitly from all co-authors.And authors whose names appear on the submission have contributed sufficiently to the scientific work and therefore share collective responsibility and accountability for the results.The authors declare that they have no conflicts of interest