基于内嵌物理信息神经网络求解空间分数阶扩散方程*

王 肖,王自强

(贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550025)

深度学习在多种应用中取得了显著的成功,然而它在求解分数阶偏微分方程中的应用直到最近才出现。文献[1]中概述了物理信息神经网络(PINN),它通过自动微分将偏微分方程嵌入到神经网络的损失中。利用PINN求解整数阶偏微分方程是非常有效的,但分数阶导数不满足自动微分的链式规则,用PINN求解分数阶导数便出现了困难。文献[2]采取把分数阶偏微分方程的非局部部分使用传统的经典数值方法进行离散后,再利用PINN进行正常的求解,得到分数内嵌物理信息神经网络算法,简称FPINN。本文将基于文献[2]中FPINN的思想建立求解空间分数阶扩散方程的FPINN方法。

本文第一部分提出了一种基于有限差分方法来离散分数阶拉普拉斯算子的数值格式。第二部分是基于FPINN求解过程设计,将方程分为自动微分与非自动微分两类算子,建立求解空间分数阶扩散方程FPINN算法。最后部分根据数值算例,验证算法的有效性。

1 数值算法的构造

本文研究的具有分数阶拉普拉斯算子的空间分数阶扩散方程如下:

(1)

其中,α∈(1,2)是空间分数阶导数的阶数,Ω∈RD,(-Δ)α/2u(x,t)采用文献[3]中的定义,如式(2):

(2)

本文采用Grunwald-Letnikov(GL)公式来逼近分数阶导数

(3)

其中,d表示x在-θ方向上到Ω边界的距离,称为反向距离。空间步长Δx=d(x,θ,Ω)/「λd(x,θ,Ω)⎤=1/λ。

将上述公式(3)代入分数拉普拉斯式定义式(2)中,然后将求积规则应用于积分上,将分数拉普拉斯式离散为如下,并推导得到n维时通项公式:

(4)

其中,Nθ表示求积点的个数,对于笛卡尔变换,定义雅可比矩阵的行列式为JD,wi1wi2…wiD-1是对应的高斯-勒让德求积权值。

为了叙述方便,取方程(1)中的Ω=[a,b],边界条件为u(0,t)=u(1,t)=0,此时

(5)

(6)

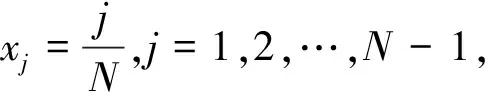
(7)

其中取ρ(x)=x(1-x),g(x)=0时,自动满足边界条件。

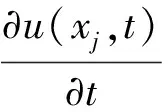
(8)

(9)

为了将上述格式简化,当λ=N时,得到如下形式

=f(xj,t)

(10)

=[f(x1,t),f(x2,t),…,f(xN-1,t)]T

(11)

对于λ=N,为了极小化误差,采用均方误差将FPINN的损失函数表示为

-[f(x1,t),f(x2,t),…,f(xN-1,t)]T

(12)

这里MSE(v)表示向量v的均方误差。

2 FPINN求解

上述将分数阶微分算子替换为离散版本,方程(1),将它分为自动微分项与非自动微分项两类算子嵌入PINN结构来解决空间分数阶扩散方程,具体操作如下:

构造方程(1)正向问题的形式为

(13)

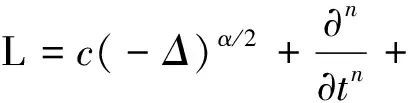
L=LAD+LnonAD

(14)

针对式(14)中的LnonAD=c(-Δ)α/2,则不满足经典的链式规则,无法利用自动微分进行求导。对于LnonAD,通过有限差分进行离散,我们用LFDM表示LnonAD的离散化版本,然后将其嵌入PINN,它的损失函数LFW(μ)定义为:

(15)

图1 物理信息神经网络(PINN)结构图

为了简要定义,我们将两层神经网络记为：

其中隐藏层(HiddenLayer)的神经元数量被记为m,σ为激活函数[6],wj为输入权重,aj为输出权重,bj为偏置项。我们把参数集记为

θ=(a1,…,am,wq,…,wm,b1,…,bm)。

3 数值算例

根据以上方法进行一系列的数值实验,以证实理论推导的正确性。

例1考虑具有精确解为

uex(x,t)=e-t·x3(1-x)3

(16)

的方程(1),相应的右端项为：

(1-x)6-α))

(17)

为了用FPINN来求解方程(1),利用DeepXDE和梯度下降Adam学习算法,将LnonAD项采用有限差分离散后的格式嵌入到PINN中,而LAD项则继续使用Tensorflow的自动微分。

并设置如下参数,以分数阶阶数α=1.8为例,激活函数σ(x)=tanh(x),Adam的学习速率为5×10-3,4个隐藏层,每个隐藏层的神经元个数为20。计算其训练误差(loss_train)和测试误差(loss_test),得到数值解对精确解的逼近度。

表1 每隔2000次的训练误差和测试误差

当α=1.8时,通过内嵌物理信息神经网络训练10000次的误差,最后的训练误差为1.67182×10-4,测试误差为1.67187×10-4。

图2 α=1.8,Δ(x)=0.05精确解与数值解

4 结语

本文以PINN为基础,结合DeepXDE新型网络框架,及神经网络梯度下降学习算法,将式(11)中的L{·}算子分为自动微分项与非自动微分项,分别嵌入到PINN中进行算法求解,提出了空间分数阶扩散方程初边值问题的FPINN算法。将上述方法应用于求解高维分数阶偏微分方程的控制问题。