基于共享近邻加权局部线性嵌入的轴承故障诊断
刘庆强, 孙艳茹, 刘远红, 吴 丽
(1. 东北石油大学 电气信息工程学院, 黑龙江 大庆 163318; 2. 大庆油田有限责任公司 天然气分公司培训中心, 黑龙江 大庆 163457)
由于机械设备的智能化发展,在检测轴承故障情况时往往有海量数据需要处理,这导致反映轴承信息的数据逐渐呈现高维特征[1-2].这不仅影响了数据的处理速度,还降低了求解精度,因此从高维轴承数据中提取显著特征变得尤为重要.近年来,流形学习算法成为故障诊断方法[3-4]中颇受关注的特征提取方式,它的主要思想是挖掘高维数据的本质结构,并在低维空间保持该结构,从而实现对数据的维数约简.其中,局部线性嵌入(local linear embedding, LLE)算法[5]是一种针对非线性数据的经典流形学习算法,可以学习任意维的低维流形,且计算复杂度相对较小,因此被广泛应用.
然而,传统LLE算法在提取特征时存在局限,如结构信息较为单一以及对离群、噪声数据敏感等问题.针对以上问题,YAO B. B.等[6]采用马氏距离代替传统邻域构建中的欧氏距离,并使用L1范数对权重矩阵进行标准化,增强了LLE的抗噪能力.WU Q.等[7]采用融合测地距离和欧氏距离的多结构拉普拉斯图进行重构降维,丰厚结构信息的同时也保持了数据的原始流形结构.K. MEHTA等[8]提出基于仿射变换的改进局部线性嵌入算法,利用近邻点的仿射组合表示高维样本数据,同时以邻域保留嵌入的方式计算低维数据,表现出较好的特征提取效果.L. ZIEGELMEIER等[9]提出稀疏局部线性嵌入算法,寻求最小化表示每个数据点所需的邻居数量,在大范围的稀疏性参数上具有较强的鲁棒性.以上算法都取得了很大的成功,但在样本邻域划分后都忽略了邻域邻居分布信息对挖掘结构的影响.同时,以上算法默认每个样本在低维嵌入中具有相同的重要性,忽略了离群点或噪声数据点对低维嵌入的影响,不利于保留原始数据的重要信息.
为解决以上问题,文中拟提出基于共享近邻的加权局部线性嵌入(weighted local linear embedding based on shared neighbors,SN-WLLE)算法.受共享近邻理论[10-11]启发,文中尝试应用共享近邻思想加强对流形局部结构的挖掘影响,在邻域划分后结合样本的6种邻居分布情况,加强多共享近邻的互近邻和单向近邻的线性重构作用,从而使LLE算法能够充分刻画样本间的内在关系.另外,文中从多流形的角度评估样本及其近邻点之间的稀疏分布一致性,进而获得样本的重要性指标,并将该信息在低维特征空间保持,从而弱化离群点和噪声点对低维嵌入的影响,并在轴承故障检测中得以应用.
1 相关工作
1.1 局部线性嵌入算法
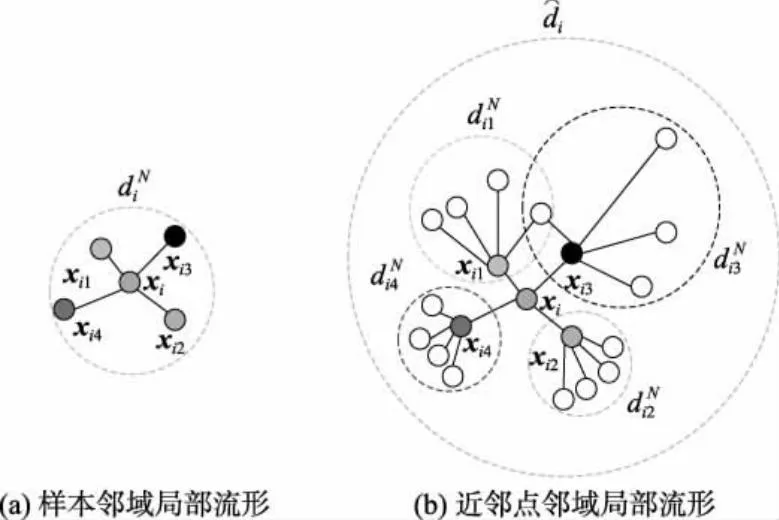
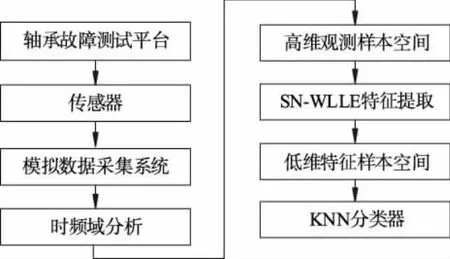
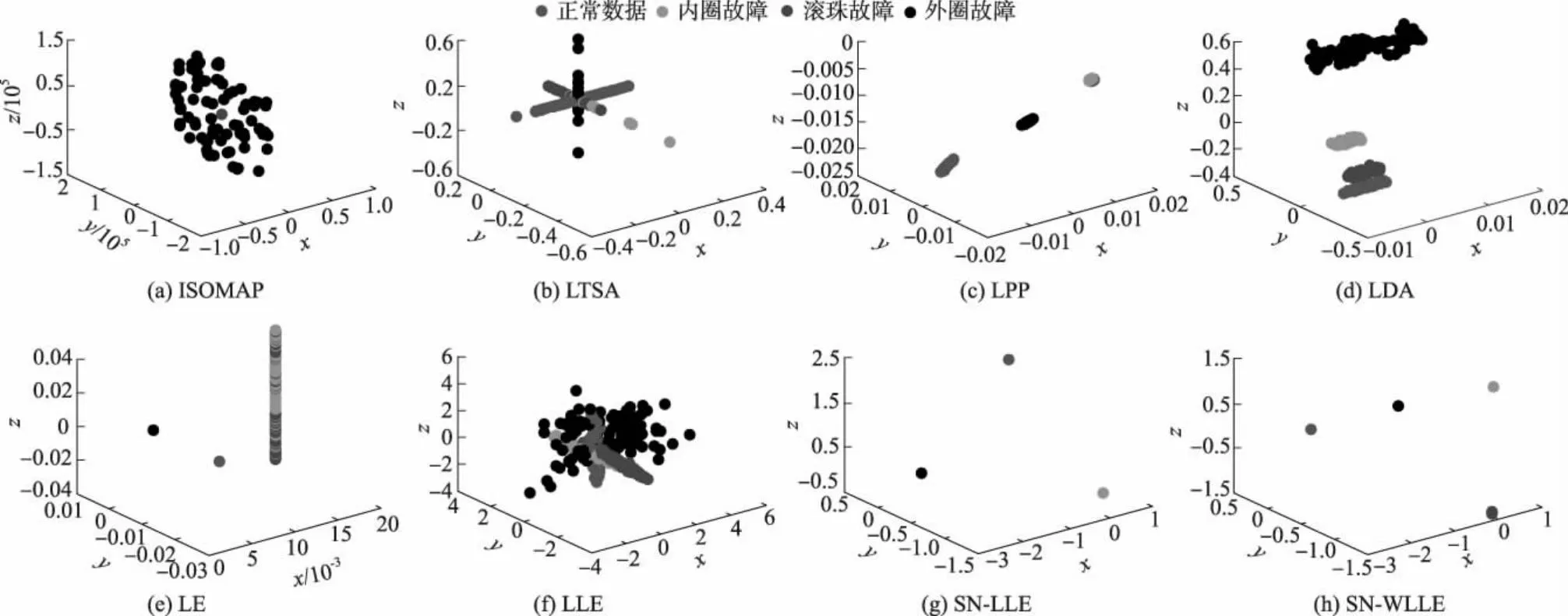
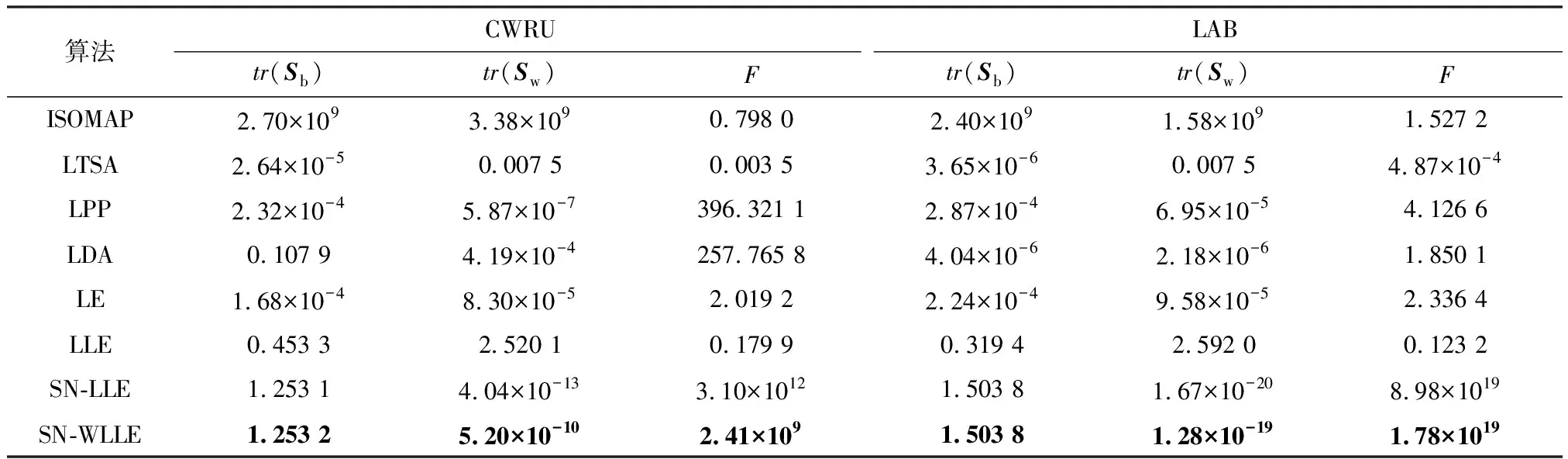
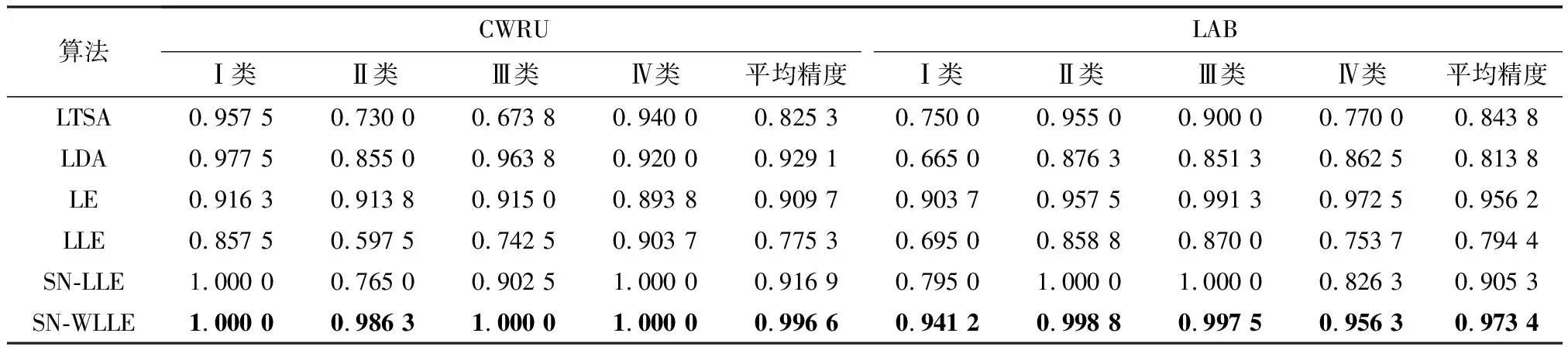
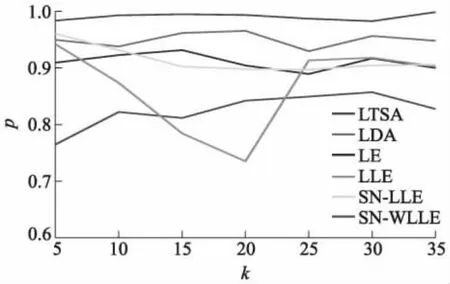
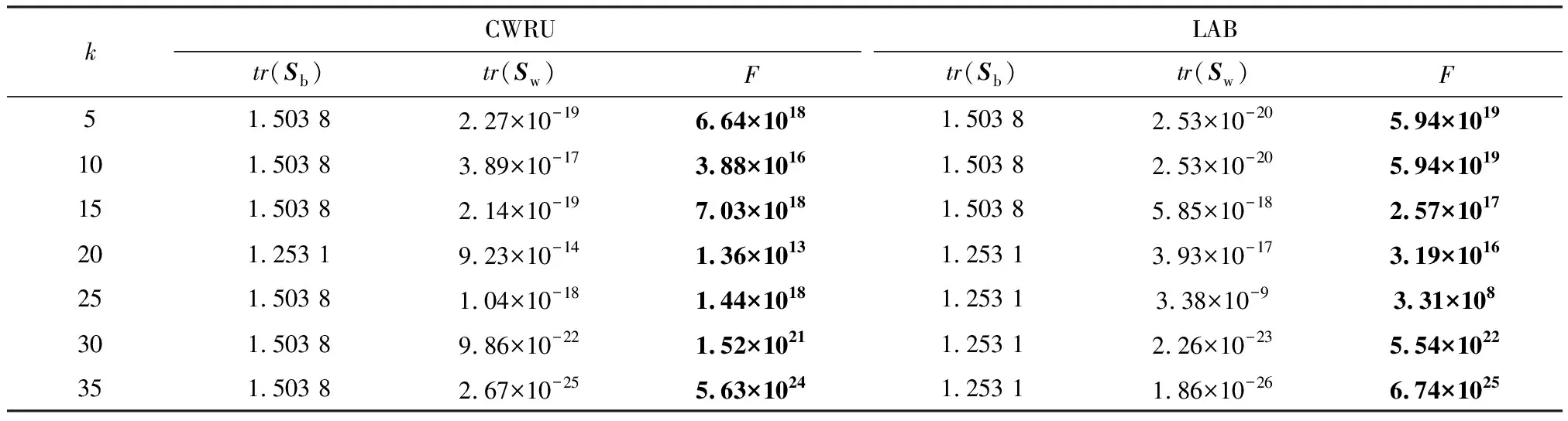
LLE算法是一种基于重构误差的经典局部流形学习算法,其核心思想是将高维空间的数据划分为多个相互交叠的局部流形,并用邻域点的线性重构权重拟合中心样本,在降维的过程中保留该重构权重结构以完成特征提取.设高维空间样本为X=[x1,x2,…,xN]∈RQ×N,其在低维空间的映射结果为Y=[y1,y2,…,yN]∈Rq×N,其中q< LLE算法流程如下: ① 划分样本邻域,通过相似距离度量样本间的相似度,各样本点取与其距离最短的k个点作为近邻点.② 计算局部重构权重W∈RN×N,各样本用其近邻点进行线性重构,通过最小化重构误差得到权重矩阵W: (1) (2) 式中:I为单位矩阵.式(2)可进一步矩阵化如下: (3) 式中:Ii、Wi分别为I、W的第i列向量,M=(I-W)(I-W)T.使用Lagrange乘子法求解式(3)可得到Y,即M的最小q个非零特征值所对应的特征向量. 余弦相似性[12]是通过测量2个向量的夹角余弦值来度量向量相似性,它体现的是方向上的相对差异,且在高维情况下依然能够保持和低维相同的性质,更适合高维空间故障向量的相似检测.样本间的余弦相似性cij定义如下: (4) 显然,cij的取值范围为[-1,1].将余弦相似性进一步投影至正空间[0,2],余弦距离dij可以表示为 dij=1-cij. (5) 传统LLE算法在邻域划分后,无论邻域的邻居分布如何,对局部结构挖掘都无影响.实际上,样本间存在6种邻居分布情况,即有(无)共享近邻的互近邻、有(无)共享近邻的单向近邻和有(无)共享近邻的非近邻情况.为获得最佳的流形结构挖掘效果,文中尝试通过样本的共享近邻结构信息来调节重构权值结构.在此引入Jaccard[13]系数定义邻域对相似度J∈RN×N,邻域对相似度越大,样本间的共享近邻结构信息也就越丰富. (6) 更进一步,共享近邻结构信息调节局部结构挖掘是以样本邻域选择为第1要则,以共享近邻结构信息为第2要则,既不忽略选邻的线性重构作用,也强调有共享近邻的样本对中心样本的线性重构作用.为此定义共享近邻调节矩阵T∈RN×N的子项为 (7) 传统LLE算法默认每个样本具有相同的重要性,忽略了对离群点或噪声数据点的处理,不利于保留原始数据的重要信息.因此,文中从多流形的角度评估样本及其近邻点之间的稀疏分布一致性,从而计算出样本在数据集中的重要程度,即样本的重要性指标.实际上,如图1所示,样本邻域可视为一个局部流形,邻域上的近邻点又在多个相互交叠的局部流形上,那么评估样本的重要性指标就可以通过样本邻域局部流形与其近邻点邻域局部流形的稀疏分布差异来表征. 图1 流形稀疏分布 样本邻域局部流形的稀疏分布程度用样本与其所有近邻点之间的平均距离表征.样本xi与其所有近邻点间的平均距离为 (8) (9) (10) 其中gi∈(0,1],gi值越大,样本的重要性也越大,反之,样本的重要性越小. 引入共享近邻结构与重要性指标后,首先在挖掘流形局部几何信息上,优化高维目标函数,提高共享近邻的k近邻信息挖掘效力,为区别原高维目标函数挖掘的权重W,设共享近邻调节的权重结构为W*,式(1)可优化为 (11) (12) 然后,在低维空间考虑样本重要性指标,优化降维后的数据信息,结合式(3)和式(10),低维目标函数由式(2)转化为 (13) 为获得标准化的低维数据,加入约束条件: (14) 进一步对式(13)进行整理,得出 (15) (16) 式中:Mg*=(Ig-Wg*)(Ig-Wg*)T.使用Lagrange乘子法求解式(16)可得到低维嵌入结果Y,即Mg*的最小q个非零特征值所对应的特征向量. SN-WLLE算法步骤如下: ① 划分邻域.结合式(4)和式(5)计算任意样本点之间的余弦距离d,对任意样本,选择距样本最近的k个样本作最近邻.② 计算局部重构权重W*.利用式(6)评估邻域对相似度J,并根据式(8)计算共享近邻调节矩阵T,结合式(1)和式(7)优化高维目标函数,计算W*.③ 计算低维嵌入结果Y.利用式(8)至式(10)评估样本重要程度,求得样本重要性指标g,结合式(2)和式(10)优化低维嵌入目标函数得到Mg*,并对其进行广义特征值分解;按照特征值λ1≥λ2≥…≥λQ,取最小q个特征值对应的特征向量组成Y. 文中提出的基于共享近邻加权局部线性嵌入的轴承故障诊断模型(SN-WLLE-KNN)如图2所示. 图2 基于共享近邻加权局部线性嵌入的轴承故障诊断模型 模型流程如下: ① 信号采集与预处理.首先通过故障试验平台进行振动信号采集,然后结合时域分析与频域分析的优势,选取轴承在不同状态下的时域特征和频域特征,包括偏度、峭度、裕度因子、均方频率、重心频率等特征,构建高维观测样本空间.② 特征提取.利用结合共享近邻与样本重要性的SN-WLLE算法对高维观测样本进行特征提取,实现对高维轴承数据的有效降维,构建低维特征样本空间.③ 故障识别.从低维特征样本空间随机选取样本,在KNN分类器中进行训练,然后利用训练好的KNN分类器进行其余样本的故障识别. 为保证模型评估的准确性,使用2组滚动轴承数据集进行评估验证,一组由凯斯西储大学(CWRU)提供,一组由实验室轴承测试平台(LAB)提供. 1) CWRU数据集.该数据集是公开的数据集,其测试平台包括一个1.5 kW的发动机、一个扭矩传感器、一个功率测试计和电子控制设备.该数据集在负载为0 kW、采样频率为12 kHz、转子转速为1 720 r/min 的情况下采集,包含正常数据、滚珠故障、内圈故障和外圈故障4类样本,每个样本维数是1 024维. 2) LAB数据集.该数据集是实验室轴承测试数据集,其平台由发动机、轴承和齿轮箱组成.该数据集在无负载、采样频率为10 kHz、转子转速为1 400 r/min的情况下采集,包含正常数据、滚珠故障、内圈故障和外圈故障4类样本,简称为Ⅰ、Ⅱ、Ⅲ、Ⅳ类,每个样本维数为1 024维. 分别在2组数据集上进行了8种算法的可视化评估试验,算法包括等距映射(isometric feature mapping, ISOMAP)、局部切空间排列(local tangent space alignment, LTSA)、局部保持投影(local preserving projection, LPP)、线性判别分析(linear discriminant analysis, LDA)、拉普拉斯特征映射(laplacian eigenmap, LE)、LLE、SN-LLE 以及SN-WLLE算法.其中SN-LLE算法为不涉及样本重要性指标的SN-WLLE拆分算法,是文中的创新算法之一.图3给出了在CWRU数据集上的降维效果. 图3 CWRU数据集上的降维效果 从图3可见, ISOMAP、LTSA、LE和LLE算法的聚类性和可分性都较差.相比前4者而言,LPP的聚类性较好,但故障特征存在交叉重叠;LDA可以完全区分故障,但聚类性不佳,外圈故障特征明显散乱;SN-LLE相较LLE有了明显改善,实现了区分3种故障的效果,从而验证了样本更深层次的共享近邻结构信息对高维几何信息的挖掘能力;SN-WLLE在SN-LLE的基础上进一步利用样本的重要性指标,优化了低维映射嵌入,以致可以完全区分4种故障,且降维效果有较好的聚类性和可分性.在LAB数据集上,SN-WLLE依然能够准确区分各类故障,表现出优于其他算法的特征提取效果. (17) 表1为2组数据集上SN-WLLE等8种算法的指标对比. 表1 不同算法的Fisher测度指标对比 由表1可见,LTSA在2组数据集上的F值都是最小的,这进一步解释了图3b中故障特征的类间交叠和类内散乱现象.LPP和LDA相较ISOMAP、LTSA、LE和LLE表现出较大的F值,但LPP的tr(Sb)值不大,存在特征交叠现象;LDA的tr(Sw)值较小,存在故障特征类内稀疏、不紧凑情况,因此这些算法都没有兼顾类内紧致性与类间可分性.而在2组数据集上,SN-LLE和SN-WLLE算法有较大的F值,且tr(Sb)值够大的同时tr(Sw)值够小,具备较好的聚类性与可分性.显然,定量评估与可视化评估结果一致,也进一步证实共享近邻结构信息和样本重要性指标信息能够提高特征提取效力. 分别在2组数据集上进行了6种算法的不同故障识别精度试验.将不同算法的低维嵌入结果输入到KNN分类器进行故障模式识别.其中,每类样本选择80%的样本进行训练,剩余20%的样本用于测试.表2给出了不同算法的不同故障识别精度对比. 表2 不同算法的不同故障识别精度对比 由表2可见,SN-WLLE在CWRU数据集上的平均故障识别精度达0.996 6,在LAB数据集上达0.973 4,且该算法对于不同故障的识别精度差别不大.另外,LLE、SN-LLE与SN-WLLE在2组数据集上的故障识别精度呈现递增趋势,这不仅表明共享近邻结构信息改善了高维空间的结构挖掘效果,也证实了样本重要性指标在低维嵌入中能够保留更多的原始重要信息. 基于传统LLE的故障检测方法对样本邻域选择较为敏感,近邻数的多少直接影响高维数据的特征提取,进而对低维空间的降维效果产生很大影响.为全面衡量SN-WLLE的鲁棒性,分别进行不同邻域参数k值的可视化评估、定量聚类评估和故障识别精度p评估试验.图4给出了不同邻域参数下的降维效果,图5给出了不同邻域参数下的不同算法识别精度对比. 图4 不同邻域参数下的降维效果 图5 不同邻域参数下的不同算法识别精度对比 从图4的降维效果可见,SN-WLLE算法表现出对近邻个数变化的非敏感性.随着k值不断增大,部分故障特征呈现短小点簇状,但始终不存在特征交叉重叠或散乱的状况,显然,SN-WLLE算法在一定邻域参数变动下,仍能够保持较好的类内紧致性和类间可分性.表3中虽然不同的k值伴有不同幅度的F值变化,但SN-WLLE算法整体有较好的F值,其聚类效果保持在108的量级水准. 表3 不同k值的Fisher测度指标 同时,由图5可见,k值的变化对SN-WLLE算法的识别精度影响不大,且相较其他5种算法,SN-WLLE算法一直保持稳定领先的高精度水准.以上3个评估试验表明,SN-WLLE算法对样本邻域选择不敏感,具备较好的鲁棒性. 1) 共享近邻结构信息与样本重要性指标能够挖掘故障数据的本质特征,通过与其他多种经典降维算法相比,SN-WLLE算法具备较好的可视化和聚类效果. 2) 将SN-WLLE算法与KNN分类器相结合建立SN-WLLE-KNN故障诊断模型,对不同状态下的轴承故障进行诊断,其识别精度最高可达1.000 0,平均故障识别精度最低可达0.973 4,诊断效果较为理想. 3) SN-WLLE算法对样本邻域选择不敏感,在一定邻域参数变动下,仍能够保持较好的类内紧致性和类间可分性,更利于模型实施故障诊断.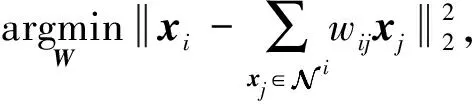

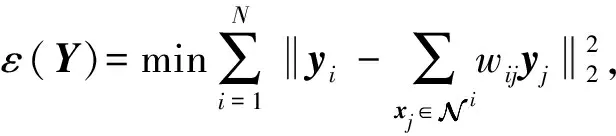

1.2 余弦距离
2 基于共享近邻的加权局部线性嵌入算法
2.1 共享近邻结构



2.2 样本重要性指标
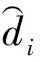
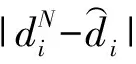
2.3 优化高低维目标函数和嵌入映射
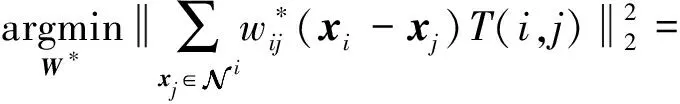
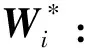
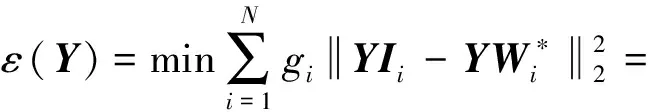
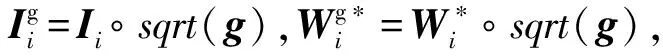
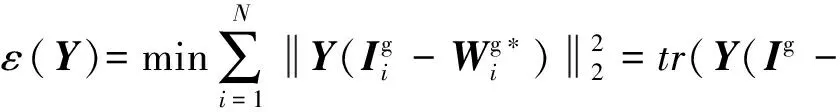
2.4 SN-WLLE算法步骤
3 基于共享近邻加权局部线性嵌入的轴承故障诊断模型
4 试验及数据分析
4.1 数据集描述
4.2 可视化评估
4.3 定量聚类评估
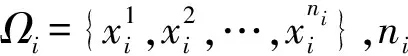
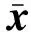
4.4 故障识别精度评估
4.5 鲁棒性评估

5 结 论

