重通法育素养 溯源头探本质——以2023年高考数学全国甲卷理科第20题的解法探究为例

肖皓月 官聖淇 张 君

(四川省温江中学)

2023年高考数学全国甲卷紧扣党的二十大报告精神,反映新时代基础教育课程理念.试题总体设计角度新颖,注重数学本质,突出理性思维,强调数学与生活及其他学科的联系,渗透数学文化,积极引导中学数学教学注重对数学学科素养的培养,发挥高考“指挥棒”作用.高考是高中课堂教学的风向标,本文以2023年高考数学全国甲卷理科第20题为例,从通性通法到秒杀解法,从不同的切入点探讨该题的解答,为解决此类解析几何试题提供参考.

2023年高考数学全国甲卷理科第20题,是一道以解析几何抛物线为背景设置的函数(最值)问题,形式新颖,综合性强,对考生的能力要求较高,特别是对高水平的考生区分较好.圆锥曲线中的最值(或取值范围)问题一直是历年高考数学试卷中的热点题型之一,常考常新,不断创新,形式各样,多以压轴题形式出现.此类问题对考生的代数恒等变形能力、数学运算能力、推理论证能力等都有较高的要求,同时突出对数学知识、数学思想方法、数学核心素养的考查,具有较好的选拔性与区分度,备受命题者青睐.

1 真题呈现

(1)求p的值;

2 真题剖析

2.1 第(1)问解法探究

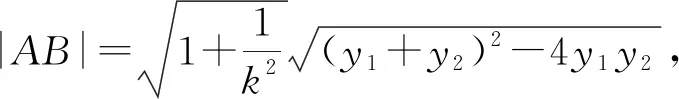
第(1)问思维导图如下:

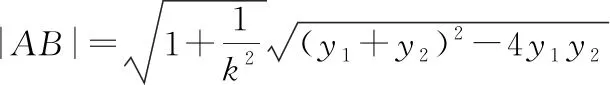
2.2 第(2)问解法探究

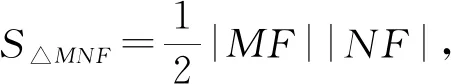
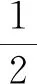
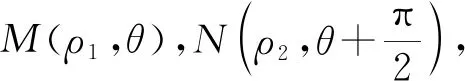
第(2)问思维导图如下:

3 解法探究

3.1 第(1)问解答

设A(x1,y1),B(x2,y2),

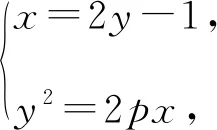
则y1+y2=4p,y1y2=2p,

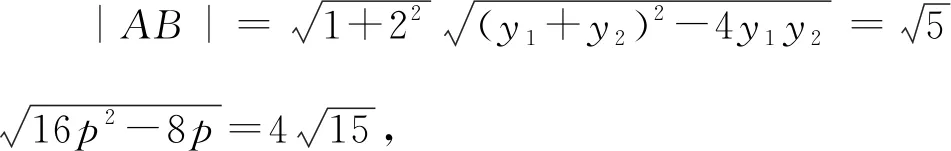
所以2p2-p-6=0.

又p>0,解得p=2.

3.2 第(2)问解答

3.2.1 思路一:综合条件,线参法化为二次函数最值

解法1：设M(x3,y3),N(x4,y4),

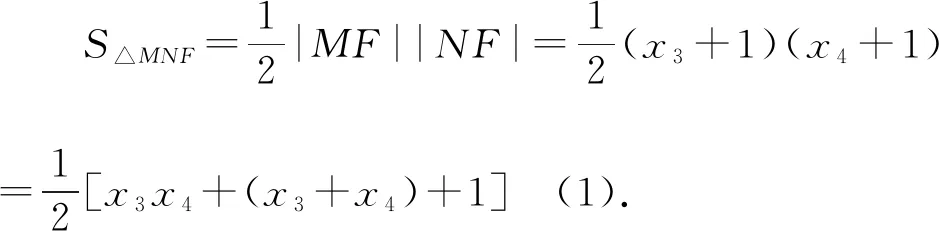
当直线MN斜率不存在的时候,设直线MN:x=s,则M(s,y3),N(s,y4),

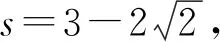
当直线MN斜率存在的时候,设直线MN:y=kx+t,

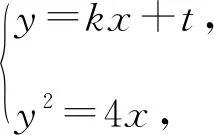
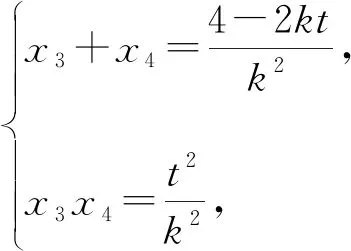
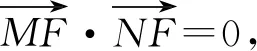
则(x3-1)(x4-1)+(kx3+t)(kx4+t)=0,

所以(x3-1)(x4-1)+(kx3+t)(kx4+t)=0,

所以(1+k2)x3x4+(kt-1)(x3+x4)+t2+1=0,

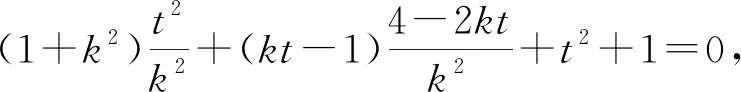
即t2+6kt+k2=4,

又t2+6kt+k2=4,

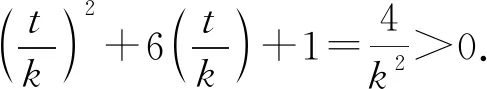
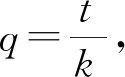
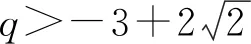
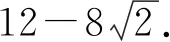
解法2：设M(x3,y3),N(x4,y4),易知直线MN斜率必不为0,则设直线MN:x=my+n,

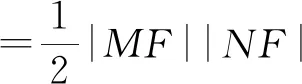
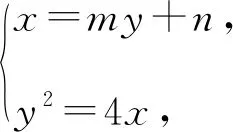
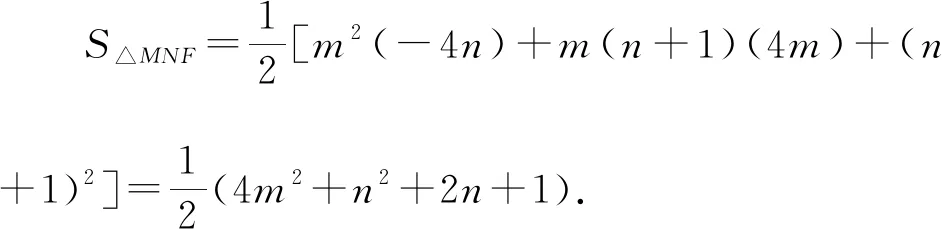
则(x3-1)(x4-1)+y3y4=0,

所以(my3+n-1)(my4+n-1)+y3y4=0,

所以(m2+1)y3y4+m(n-1)(y3+y4)+(n-1)2=0,

所以(m2+1)(-4n)+m(n-1)(4m)+(n-1)2=0,

所以4m2=n2-6n+1,

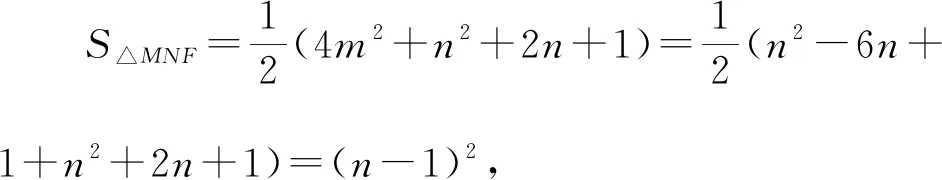
又4m2=n2-6n+1≥0,

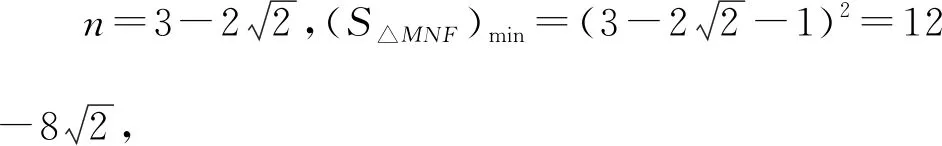
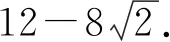
解法3：设M(x3,y3),N(x4,y4),易知直线MN斜率必不为0,则设直线MN:x=my+n,

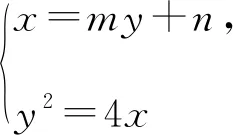
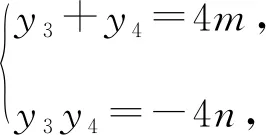
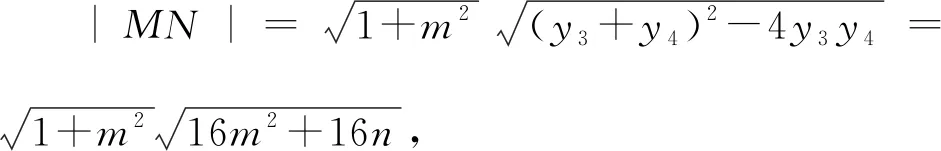
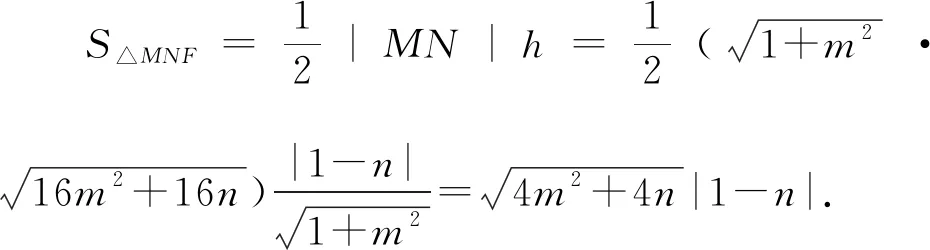
又有解法2知4m2=n2-6n+1,

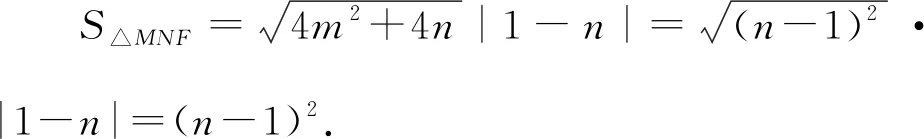
以下同解法2.

解法4：设M(x3,y3),N(x4,y4),易知直线MN斜率必不为0,则设直线MN:x=my+n,则设直线MN与x轴交于Q(n,0).

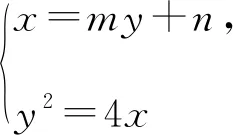
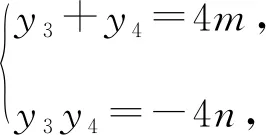
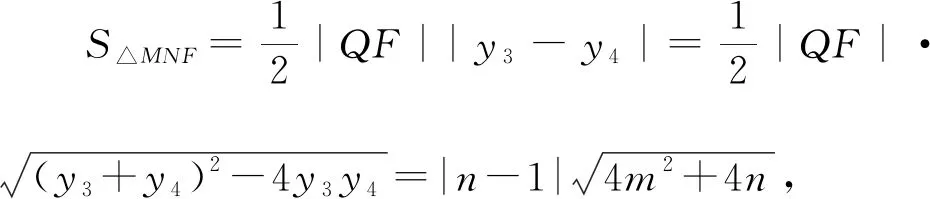
以下同解法3.

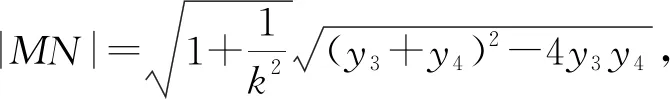
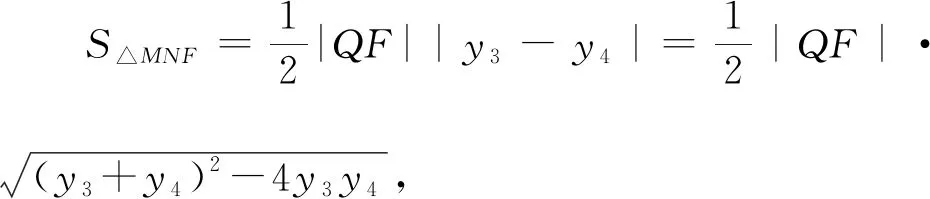
思路一主要思想是设直线方程,最终转化为二次函数最值问题.

3.2.2 思路二:点参法转化函数最值问题

解法5：设M(x3,y3),N(x4,y4),

则(x3-1)(x4-1)+y3y4=0,

则x3x4-(x3+x4)+1+y3y4=0.

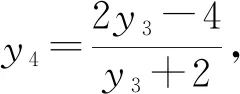
则由三角形面积的坐标式可得:

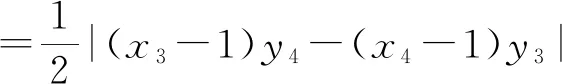
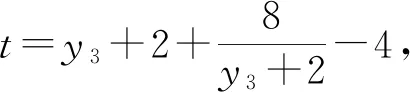
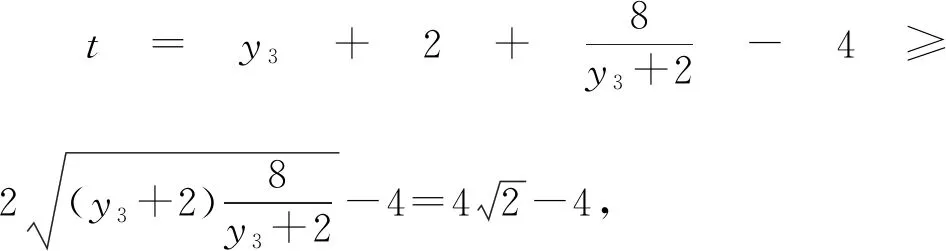
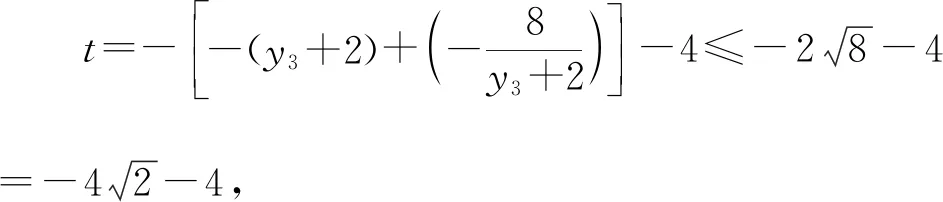
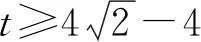
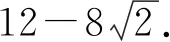
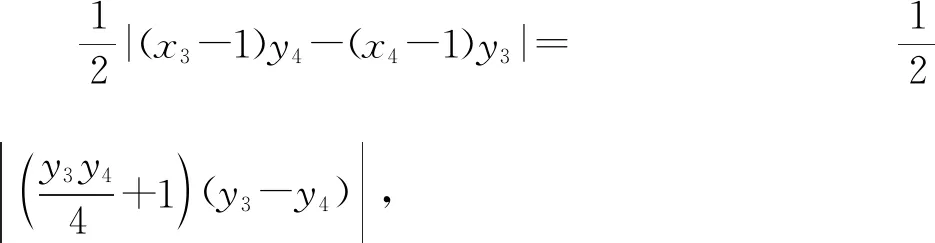
3.2.3 思路三:合理运用条件,引入角度参数

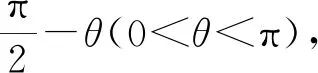
由抛物线定义,|MF|=|MF|cosθ+2,

又t2=(sinθ-cosθ)2=1-2sinθcosθ,

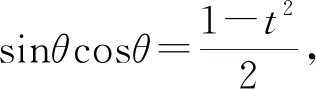
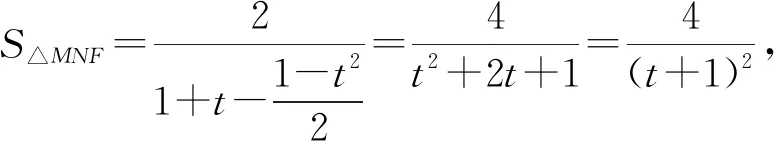
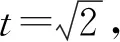
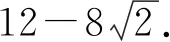
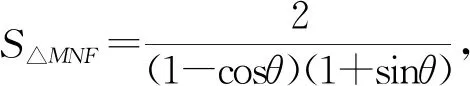
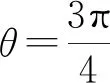
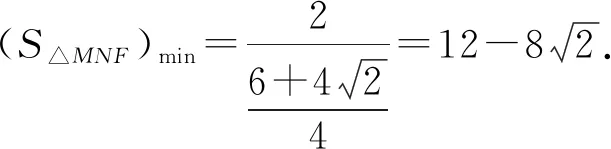
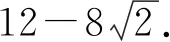
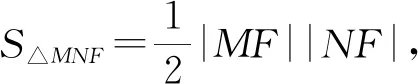
3.2.4 思路四:极坐标法简化运算

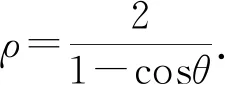
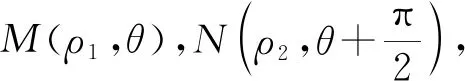
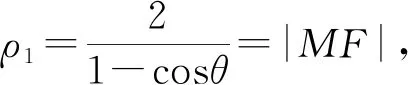
又t2=(sinθ-cosθ)2=1-2sinθcosθ,

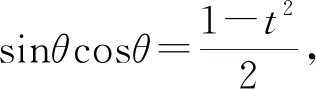
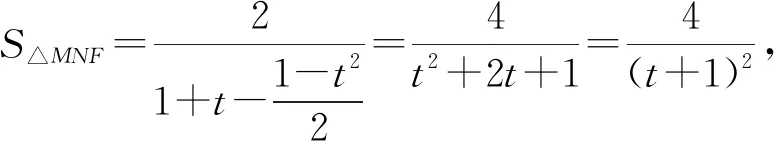
以下同解法6.

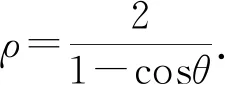
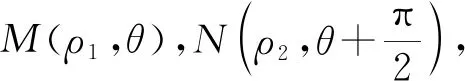
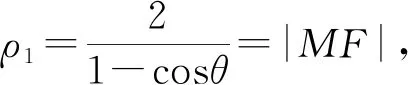
要求S△MNF的最小值,即求(1-cosθ)(1+sinθ)的最大值.

以下同解法7.

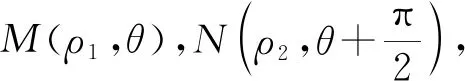
4 追本溯源

圆锥曲线中面积最值问题是高考中的热点和难点问题,此类问题常与函数、三角、不等式等知识有机结合综合考查.此题解法一方面注意选取合适的面积公式,从而求得面积表达式.另一方面要合理使用条件将面积表达式转化为函数问题,我们可以追溯到2015浙江高考19题,读者可仿照上文中解法给出第(2)问对应的解法.

(1)求实数m的取值范围;

(2)求△AOB的面积最大值(O为坐标原点).

5 题后反思

这道高考题,考察抛物线中三角形面积最值问题,以抛物线为载体,将抛物线、三角形、函数等多项内容结合起来考察知识、思想方法、能力综合功能,对学生数学素养要求较高.知识方面:考察直线方程、韦达定理,弦长公式、点到直线距离、三角形面积公式、抛物线定义与性质、基本初等函数(二次函数、基本初等函数、三角函数等)性质,基本不等式等多项知识;思想方法方面:考察到函数与方程、数形结合、化归与转化、分类讨论数学思想;能力方面:考察数学运算能力、直观想象能力、逻辑推理能力、数据处理能力.

圆锥曲线面积最值问题本质其实就是函数最值问题,解决此类问题常分两步:第一步:选择合适的面积公式.可用公式法或割补法或者坐标法求取三角形面积.第二步:转化为函数最值问题.这一步也尤为重要,一方面我们可以选择线参法或者点参法,将面积转化为双元问题,然后根据题设条件,寻求双元之间关系,转化为单元问题,最终转化为函数最值问题.另一方面,在一些情况下若涉及焦半径等,可以选择角度为参数或者极坐标法,直接将面积转化为单元问题,极大减轻计算量.

数学教学中,解决此类问题,教师应把握问题本质,落实素养导向.应引导学生多角度多方法进行探索,感悟其中的变与不变,总结多种解题方法,感悟其中数学思想.重视通法,培养数学素养,追根溯源,探索问题本质!