导数压轴题的多视角解法探究及其背景溯源——以2023年天津卷与全国甲卷文科导数压轴题为例

郭 蒙

(陕西省榆林市吴堡中学)

本文以多视角探究2023年天津卷高考数学与全国甲卷文科数学导数压轴题的解法,揭示试题背后的背景,这两道题综合性强,区分度高,满足了高考选拔高层次人才的要求,非常有必要探究.

1.高考试题呈现

(1)当a=1时,讨论f(x)的单调性;

(2)若f(x)+sinx<0,求a的取值范围.

(1)求曲线y=f(x)在x=2处切线的斜率;

(2)当x>0时,证明:f(x)>1;

甲卷文科导数题将导数与三角函数巧妙地结合起来,通过对导函数的分析,考查函数的单调性等相关问题,通过导数、函数不等式等知识,深入考查了分类讨论、化归与转化的思想,难度较大.甲卷第一问,天津卷前两问都属于基础题,试题难度上进行了合理控制,体现了学科知识本质的基础性,落实了高考内容改革,考查学生对基础知识和基本方法的深刻理解及融会贯通的应用.甲卷(2)问聚焦学科核心素养,立意新颖,计算量大,巧妙地将一次函数、三角函数与函数的单调性等融合在一起,创新性极高.天津卷(3)问以斯特林公式、阶乘等价量为背景,第三问继前一问函数不等式进行应用,结合数列单调性思想,体现了函数与不等式的和谐统一,彰显了试题的综合性.

2.解法探究

2.1 甲卷试题解法探究

2.1.1 第(1)问的解法

2.1.2 第(2)问的证明

结论1：若f(x)≥0在[a,b](a,b为常数)上恒成立,且f(a)=0(或f(b)=0),则f′(a)≥0(或f′(b)≤0).

【证明】因为f(x)≥0在[a,b]上恒成立,且f(a)=0,所以存在t∈(a,b],使得f(x)在[a,t]上单调递增,因此f′(x)≥0在[a,t]上恒成立,故f′(a)≥0.(f′(b)≤0证明方法类似)

结论2：若f(x)≥0在[a,b](a,b为常数)上恒成立,且f(a)=0,f′(a)=0(或f(b)=0,f′(b)=0),则f″(a)≥0(或f″(b)≤0).

【证明】因为f(x)≥0在[a,b]上恒成立,且f(a)=0,所以存在t∈(a,b],使得f(x)在[a,t]上单调递增,因此f′(x)≥0在[a,t]上恒成立,又因为f′(a)=0,所以存在δ∈(a,t],使得f′(x)在[a,δ]上单调递增,因此f″(x)≥0在[a,δ]上恒成立,故f″(a)≥0.(f″(b)≤0证明方法类似)

【评注】端点效应是必要性探路的一种特殊情况,利用端点效应求出的参数范围并不一定就是所求的实际范围,必须检验充分性.利用端点效应可以缩小参数的讨论范围,减少分类讨论的类别,降低思维的成本.

解法一(端点效应)

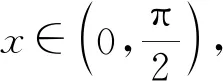
【评注】本题可利用端点效应求解,并且证明充分性成立,即可证明充要性,2016年全国Ⅱ卷文科第20题,2017年全国Ⅱ卷文科数学第21题,2019年全国Ⅰ卷文科数学第20题,2022年全国Ⅱ卷第22题都可利用端点效应完美解答.利用端点效应可缩小参数的范围,使得分类讨论的问题得到简化,端点效应为我们用分类讨论解题提供了参数的分界点.

解法二(连续函数保号性)

当a≤0时,由解法一的充分性可知,满足题意.

【评注】利用必要性探路可得到参数的分界点,以此分界点进行分类讨论,进而完美的解答了此题.

解法三(零点存在定理)

【评注】此解法计算量较大,要求学生要有较强的数学运算能力,参数a的分界点可以利用端点效应得到,当a>0时,我们用零点存在定理推导出矛盾.高考导数题,命题人更倾向于考查学生分类讨论思想的运用能力.

解法四(切线放缩法)

【评注】本解法要求学生具有较强的数学运算能力,当a>0时,利用切线放缩,推导出矛盾,进而得出参数的取值范围.

解法五(分离参数)

【评注】本题参数a容易分离出来,但导函数比较复杂,为了得到导函数的符号,我们又构造了函数m(x),利用导数得到了m(x)>0,进而得到了h(x)为单调递增函数,再利用导数定义求出了参数a的范围,完美避开了由洛必达法则计算极限的问题.

解法六(凹凸性)

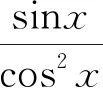
【评注】借助函数凸凹性以及切线斜率几何意义,极大地简化了问题,使得问题迎刃而解,提升了学生的直观想象、逻辑推理等核心素养.

2.2 天津卷试题解法探究

2.2.1 第(1)问的解法

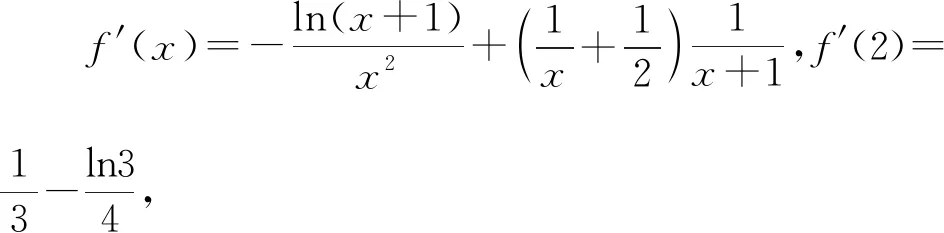
【评注】第(1)问属于常规题型,突出基础性要求.

2.2.2 第(2)问的证明

证法一(对数单身狗)

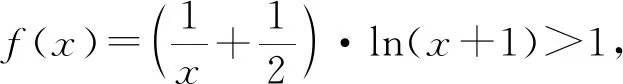
【评注】利用“对数单身狗”,将对数型函数独立出来,构造函数,只需求一次导数,就可以证明不等式,降低了试题难度.

证法二(二阶导数)

【评注】利用二阶导数证明此不等式,难度大于方法一,从中也能看出对数单身狗可以降低试题难度,简化解题过程.

2.2.3 第(3)问的证明

证法一(数列单调性)

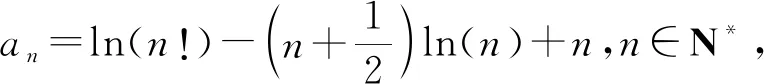
【评注】第(3)问右边等式比较容易证明,由于1=a1,猜测{an}单调递减,因此只需证明{an}是递减数列即可.

证法二(飘带放缩)

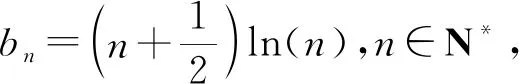
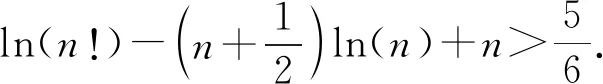
证法一(飘带放缩)

证法二(拆和法)

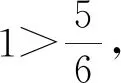
证法三(构造函数)

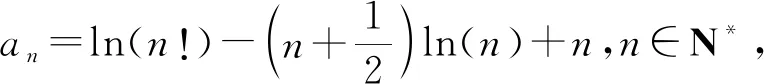
【评注】利用第二问的结论,构造函数,将不等式放缩,再利用裂项相消法,证明了不等式,ln2≈0.693.

证法四(帕德逼近)

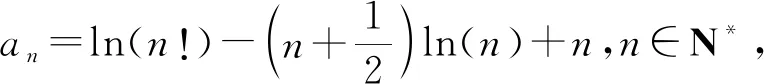
2.3 背景溯源

甲卷解法七(泰勒公式)

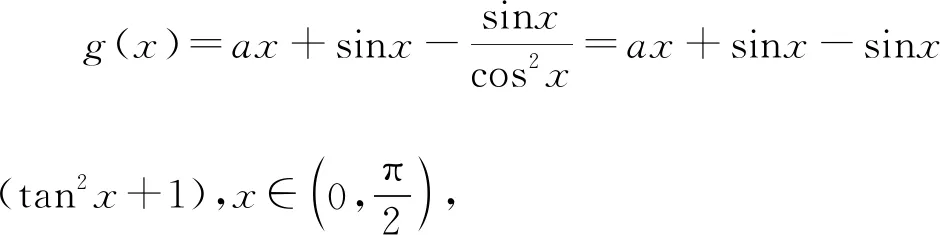
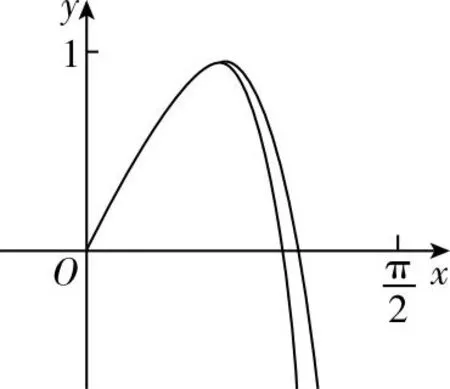
【评注】泰勒公式为我们解题提供了新的视角,并且可以明确出题人的命题思路,看透题目的本质,以泰勒公式为背景命题,立意新颖,创新性极高,为学生高等数学的学习做铺垫,具有选拔人才的作用,利用高观点可以溯其源,究其本,在学习中可以适当给学生渗透相关知识,这样可以让师生深入剖析试题,准确把握命题的方向.在考试中,可以利用泰勒公式迅速得到参数的答案,做到心中有数,利用分类讨论等方法完美解答问题.

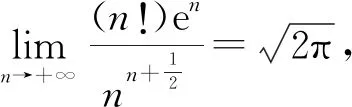
天津卷证法五

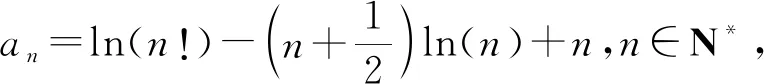
【评注】斯特林公式为我们解题提供了新的视角,并且可以明确出题人的命题思路,看透题目的本质,以斯特林公式为背景命题,立意新颖,创新性极高,为学生高等数学的学习做铺垫,具有选拔人才的作用,利用高观点可以溯其源,究其本,今年这道高考题解法很多,读者可以尝试用数学归纳法等方法解答,ln2≈0.693,ln3≈1.099.

3.结语

2023年甲卷这道高考题,将三角函数、导数紧密联系起来,是一道非常精彩的压轴题,难度较大,创新性极高,真正起到了高校选拔性考试的作用.端点效应是解决含参数不等式恒成立问题的一个有力武器.天津卷高考导数压轴题,经常引入高等数学背景下的数学问题,如2017,2019,2020,2022年分别以刘维尔不等式、拉格朗日中值定理、函数凹凸性、柯西不等式为背景,高等数学是初等数学的延伸和发展,高考作为高校的选拔性考试,一直关注两者的衔接,在交汇点命题,这样设计的试题,立意高远,角度新颖,可以高屋建瓴地看问题.通过多种视角探究问题,培养学生的发散思维能力和创新精神,提高学生的解题能力,培养和发展学生的逻辑推理、数学运算等核心素养.用高观点来指导高中数学的教学是很有必要的,高等数学与高中数学的有机结合,将问题化难为易.很多问题只有在高观点下才能理解得更深刻,才能探索出数学问题的本质,因此在高三复习阶段,师生应重视基础,通过数形结合感受性质,重视导数与三角函数、数列等多元的融合,适当渗透高观点去探究问题的本质,开阔解题思路,提高学生分析问题,解决问题的能力,进一步提升学生的数学学科素养,希望本文对读者的学习有一定的启发作用.