基于分数阶理论的两端固定杆热弹动力响应
郭 颖,杜 翠,马建军
(1.河南科技大学 a.土木建筑学院;b.机电工程学院,河南 洛阳 471023;2.成都信息工程大学 软件工程学院,四川 成都 610000)
0 引言
Biot[1]提出的耦合热弹性理论存在2个不足,一是该理论忽略了温度对弹性变化的影响;二是由于热方程是抛物线形的,其预测的热波传播速度是无限大的,这与事实不符。为了弥补这些不足,学者们提出了不同的热弹性理论,主要有:Lord-Shulman (L-S)[2]广义热弹性理论、Green-Lindsay (G-L)[3]广义热弹性理论以及Green-Naghdi (G-N)[4-6]广义热弹性理论。基于上述理论,学者们进行了大量研究[7-13],分析了弹性、黏弹性介质以及功能梯度材料中多维热弹应力应变问题,探讨了材料物性参数以及外荷载作用对各物理量的影响。
移动热源在冶金过程中充当着重要的角色,特别是在焊接过程中。文献[14-15]基于广义热弹性理论,研究了考虑移动热源影响的两端固定杆的热弹/电磁热弹问题。文献[16-17]考虑移动热源的影响,分析了中空圆柱的多物理场耦合动力响应问题。文献[18]研究了二维轴对称无限圆柱体在移动热源影响下的热弹耦合问题。文献[19]分析了运动热源和简谐热作用下无限长中空圆柱的热弹性耦合响应。文献[20]对柱体类工件在移动热源作用下温度场特性进行了分析。上述研究虽然考虑了移动热源,但没有考虑材料本身的特性以及温度对材料特性的影响。
通常情况下材料的弹性模量、热传导率等特性参数会与温度有一定的相关性,从而影响介质的热弹力学行为。文献[21]研究了具有温度相关材料性能的功能梯度复合材料的热应力问题。文献[22]基于G-L广义热弹性理论,研究了热冲击作用下材料特性参数与温度相关特性之间的关系。文献[23]基于G-N理论,研究了平面波在各向同性且与温度相关的半无限大介质中传播的问题。文献[24]基于三相滞后热弹性模型分析了热冲击作用下平面波在弹性半空间自由表面与温度相关的反射问题。文献[25]建立了可预测纳米结构在极端环境下的热弹性行为的非局部热弹性模型,分析了瞬态热对非局部参数和温度相关导热系数的影响。
Abel将分数阶积分算子应用于求解等时曲线的积分问题中[26],随后,学者们发现分数阶与整数阶具有一定的自相似性,分数阶广义热弹性理论得以快速发展。常用的分数阶热弹性理论有:Sherief[27]型分数阶广义热传导理论、Youssef型分数阶广义热传导理论[28]、Ezzat型分数阶双相滞后广义热传导理论[29]和Ezzat型分数阶三相滞后广义热传导理论[30]。文献[31]推导出了考虑2个不同热松弛时间因子的分数阶广义热弹性理论。文献[32-33]分析了分数阶理论下弹性/黏弹性介质的动力响应问题。文献[34]采用Sherief型分数阶广义热传导理论研究了受移动热源作用的两端固定杆热弹耦合问题。文献[35-36]基于不同分数阶广义热弹性理论,研究了多种材料特性参数与温度相关的热弹/电磁热弹耦合动力响应问题。文献[37-38]考虑了受移动热源作用的三维热弹耦合问题,了解了热源移动速度对耦合问题的影响。文献[39-41]基于不同分数阶理论,结合移动热源以及多种复杂边界条件,研究了3种杆件的多物理场耦合动力响应。文献[42]提出了考虑材料记忆依赖效应和空间非局部效应的非局部广义热弹扩散耦合理论。
上述研究中,已有采用不同的分数阶积分算子分析介质的热弹动力响应问题和材料特性对介质影响的研究,但同时考虑分数阶积分和2个热松弛时间因子分析材料特性与温度相关介质的热弹耦合问题尚不多见,特别是将2个热松弛时间因子同时引入分数阶广义热弹性理论对问题进行求解更为少见,而分数阶积分算子的引入可以更为清晰地描述热波在介质中的传播情况,消除原本广义热弹性理论难以描述的问题。为了能更好地分析不同参数对各无量纲物理量的影响,本文将Ezzat型分数阶广义热弹性理论和G-L广义热弹性理论相结合,建立同时考虑分数阶参数和2个热松弛时间因子的分数阶广义热弹动力理论,基于该理论建立可描述两端固定杆温度场、应力场和变形场等多物理场耦合的数学模型,借助拉普拉斯(Laplace)积分变换及其数值反变换的方法得到无量纲位移、应力和温度的分布规律,分析分数阶参数、2个不同的热松弛时间因子、温度相关性参数以及移动热源传播速度对无量纲位移、应力和温度的影响。
1 基本控制方程
基于Ezzat型分数阶广义热弹性理论和G-L广义热弹性理论的基本控制方程[31,34]为:
(1)
其中:σij为应力分量;λ和G为拉梅(Lamé)常数;β1=(3λ+2G)αt,αt为线性热膨胀系数;εij为应变分量;τ0为第1个热松弛时间因子;θ=T-T0,T为绝对温度,T0为参考温度;δij为克罗内克(Kronecker)记号;α为分数阶参数且0<α≤1。
(2)
其中:逗号后的下标表示对坐标求导;字母上方的点表示对时间求导;ρ为质量密度;ui为位移分量。
(3)
(4)
其中:qi为热流向量分量;η为熵密度;Q为热源。
(5)
其中:CE为比热。
(6)
其中:κ为热传导系数;τ1为另1个热松弛时间因子。
上述方程中考虑了如下的温度相关性参数λ=λ0f(T),G=G0f(T),κ=κ0f(T),β1=β10f(T),其中,λ0,G0,β10和κ0均为与温度无关的特性参数,f(T)为与温度相关的一维函数,当f(T)=1时,则表明与温度不相关[43]:
f(T)=1-ζT。
(7)
f(T)≈1-ζT0,
(8)
其中:ζ为与温度相关的经验常数。
2 问题描述
基于Ezzat型分数阶广义热弹性理论和G-L广义热弹性理论,研究一维两端固定杆受到移动热源影响的热弹性瞬态响应问题。对于一维问题,沿杆轴线方向建立一维坐标系,则有非零位移分量ux=u(x,t),方程(1)~方程(5)可简化为如下形式:
(9)
结合方程(2)和方程(9),可得:
(10)
考虑分数阶参数影响的广义能量方程:
(11)
为了后续计算方便,引入如下无量纲量:
(12)
利用上述无量纲量,对方程(9)~方程(11)进行无量纲化,为了方便起见,将无量纲化后方程中字母上标的星号去掉,可得:
(13)
(14)
(15)

问题的初始条件:
(16)
问题的边界条件(假设杆的长度为l且两端绝热):
(17)
杆在移动热源的作用下需要考虑热源移动速度和热量,其中,υ为热源移动速度,是1个沿x轴正方向移动的常数,经过无量纲得:
Q=Q0δ(x-υt),
(18)
其中:Q0为移动热源大小;δ为delta函数。
3 拉普拉斯域中问题求解
引入拉普拉斯变换公式:
(19)
其中:s为拉普拉斯变换中的变换因子。
利用上述拉普拉斯变换公式,方程(13)~方程(15)可变为:
(20)
(21)
(22)
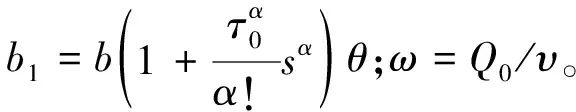
对边界条件进行拉普拉斯变换得:
(23)
(24)
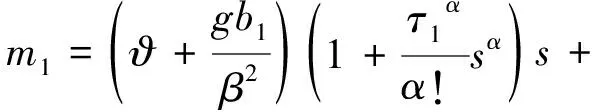
方程(24)的通解为:
(25)
其中:Ci(i=1,2,3,4)是与变换因子s相关的1组待定系数。C5的表达式如下:
(26)
其中:±k1和±k2是方程(27)的特征根。
k4-m1k2+m2=0,
(27)
可表达为:
(28)
(29)
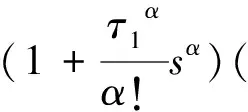
方程(29)的通解为:
(30)
其中:Cii(i=1,2,3,4)是与变换因子s相关的另1组待定系数。
将方程(25)和方程(30)代入方程(21),可得到如下关系:
(31)
根据边界条件方程(23),可得:
C1+C2+C3+C4=-C5;
(32)
C1e-k1l+C2ek1l+C3e-k2l+C4ek2l=-C5e-(s/υ)l;
(33)
-C11k1+C22k1-C33k2+C44k2=(s/υ)C55;
(34)
-C11k1e-k1l+C22k1ek1l-C33k2e-k2l+C44k2ek2l=(s/υ)C55e-(s/υ)l。
(35)
联立方程(32)~方程(35),可得:
(36)
将方程(36)代入方程(25),可得:
(37)
结合方程(31)和方程(36),可得:
(38)
将方程(38)代入方程(30),可得:
(39)
将方程(37)和方程(39)代入方程(20),可得:
(40)
4 数值反变换

(41)
其中:Re为实部;i为虚数单位。为了能加速收敛,结合大量已有试验和现有计算结果,β应满足βt≈4.7[44]。
5 数值结果及分析
为了进行数值计算,除了引入方程(40)进行数值拉普拉斯反变换,得到时域内杆的无量纲位移、应力和温度,还需要引入材料特性相关的参数:λ=7.76×1010Nm-2,G=3.86×1010Nm-2,ρ=8 954 kgm-3,αt=1.78×10-5K-1,CE=383.1 J kg-1K-1,κ=386 Wm-1K-1,T0=293 K,ζ=0.000 5 K-1,Q0=10,l=10。
数值计算得到了杆中无量纲位移、应力和温度的分布规律。计算中,研究了分数阶参数α、2个不同的热松弛时间因子τ0和τ1、温度相关性参数ϑ以及移动热源传播速度υ对无量纲位移、应力和温度分布规律的影响效应,数值计算分析分别考虑4种不同的情形,每种情况分数阶参数均为α=0.25和α=1.0。4种不同的情形如下:(1)τ1=0.05时,τ0分别取值τ0=0.03,τ0=0.06,τ0=0.09;(2)τ0=0.03时,τ1分别取值τ1=0.05,τ1=0.1,τ1=0.15;(3)τ0=0.03和τ1=0.05时,ϑ分别取值ϑ=0.5,ϑ=1.0,ϑ=1.5;(4)τ0=0.03和τ1=0.05时,υ分别取值υ=1.0,υ=2.0,υ=3.0。所得结果如图1~图4所示。
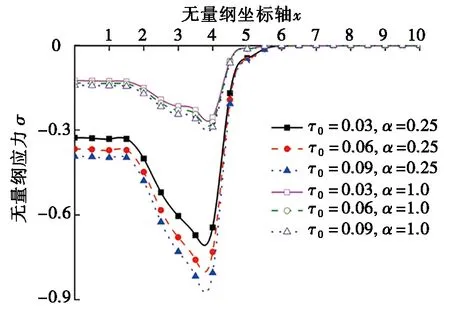
(a) 分数阶参数下τ0变化对无量纲位移的影响
图1中给出了分数阶参数和热松弛时间因子τ0变化对无量纲位移、应力和温度的影响。从图1a和图1b可以看出,无量纲位移和应力随分数阶参数增大逐渐减小,而随热松弛时间因子的增加而增大。随着热源的移动,图1a中杆产生了沿杆轴向的热膨胀变形,热扰动区域基本保持不变。随着分数阶增大,热松弛时间因子对位移和应力产生的影响逐渐不明显。图1c中仅可以在曲线峰值出看出分数阶参数变化对无量纲温度的影响,但热松弛时间因子τ0变化对无量纲温度的影响不明显。
图2给出了分数阶参数和热松弛时间因子τ1变化对无量纲位移、应力和温度的影响。从图2中可以看出:当分数阶参数α=1.0时,热松弛时间因子τ1变化对各无量纲物理量均有一定影响,但影响不明显。图2a形式分数阶参数α=0.25时,热松弛时间因子τ1变化对无量纲位移影响也比较小。从图2b和图2c中可以看出:当分数阶参数α=0.25时,无量纲应力和温度曲线峰值和谷值处,热松弛时间因子τ1变化影响明显,随着热松弛时间因子τ1增大,无量纲应力和温度逐渐增大。
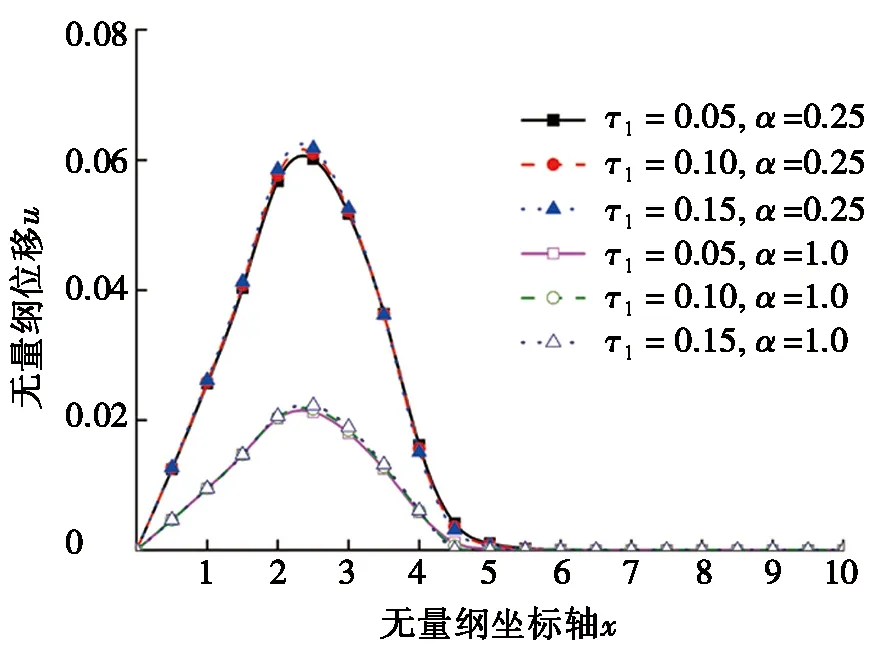
(a) 不同τ1和α时无量纲位移分布情况
图3中给出了分数阶参数和温度相关性参数ϑ变化对无量纲位移、应力和温度的影响。除无量纲温度外的所有物理量受分数阶参数和温度相关性参数均非常明显。图3a中,随着温度相关性参数ϑ增大,位移逐渐减小,其峰值逐渐向着z=0处移动,且产生的热扰动区域也在逐渐减小。图3b显示除了热扰动区域逐渐减小外,随着温度相关性参数增大曲线在z=0处明显减小。从图3c中可以看出:分数阶参数和温度相关性参数对温度的影响不大,随着分数阶参数增大,温度相关性参数对无量纲温度的影响更不明显了。
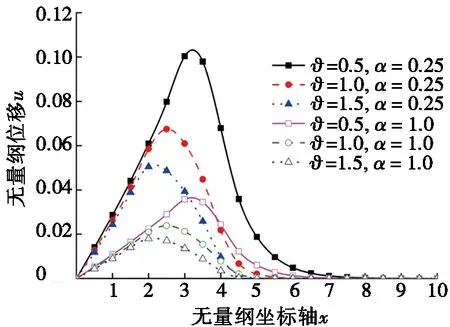
(a) 考虑α影响时ϑ变化对无量纲位移的影响
图4给出了分数阶参数和移动热源传播速度υ变化对无量纲位移、应力和温度的影响。与图1~图3类似的是,分数阶参数对无量纲温度影响不明显。图4a和图4b显示随着移动热源传播速度υ增大,无量纲位移和应力曲线逐渐减小,但扰动区域逐渐增大,且峰值向后移动。从图4c可以看出:随热源移动速度增大,无量纲温度逐渐减小,主要是因为在相同的时间段内,热源释放出相同的热量,然而随着热源速度的不断增加,单位长度所释放出的热量密度降低造成的。

(a) 分数阶参数下不同速度对无量纲位移的影响
此外,本文公式和程序中取τ0=0和ζ=0时,可将模型退化成与参考文献[34]相同的模型,并将本文退化结果与文献[34]的相应结果进行对比。结果见图5。图5a~图5c表明:当τ0=0、ζ=0和α=0.25时,可得到与文献[34]吻合较好的计算结果,有微小差异是由于数值计算方法的不同引起,其中最大偏差为9.98%,平均偏差为1.8%。从而进一步验证了本文计算结果的正确性和合理性。
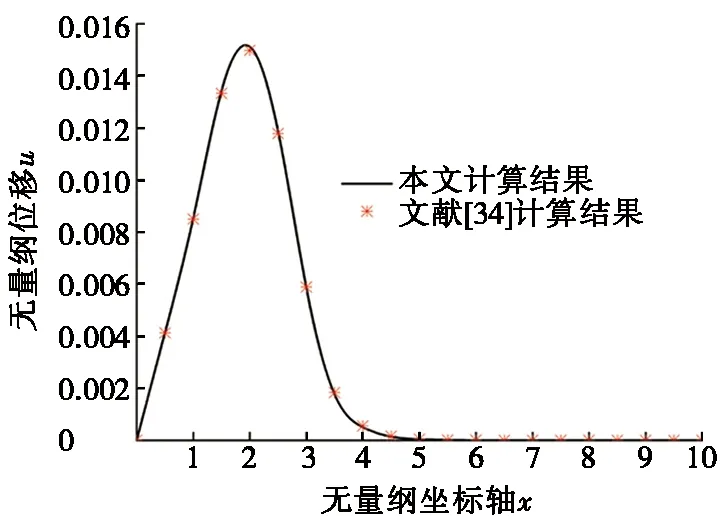
(a) 无量纲位移与文献[34]结果的比较
6 结论
本文基于Ezzat型分数阶广义热弹性理论和G-L广义热弹性理论,借助拉普拉斯积分变换及其反变换法研究了移动热源作用下两端固定的温度相关性杆一维热弹动力响应问题,得到了无量纲位移、应力和温度沿x方向的分布情况,研究了分数阶参数、2个不同的热松弛时间因子τ0和τ1、温度相关性参数以及移动热源传播速度对各无量纲量的影响。结果表明:
(1)分数阶参数对各物理量均有一定的影响,但对无量纲位移和应力的影响更明显,分数阶参数会对无量纲量产生一定的滞后影响。
(2)热松弛时间因子τ0对无量纲温度外的其他2个物理量影响显著,而热松弛时间因子τ1仅对无量纲温度的影响最为显著,分数阶参数增大使得2个热松弛时间因子对3个无量纲物理量的影响逐渐减小。
(3)温度相关性参数和移动热源传播速度对3个无量纲量影响非常明显,不仅影响曲线峰值的大小,对杆的扰动区域影响也十分明显。

