桥面运动对多索索网-阻尼器系统阻尼比的影响研究

李浚东，王荣辉，甄晓霞，刘桂源

(华南理工大学土木与交通学院,广州 510640)

引言

斜拉桥拉索以及悬索桥吊索在外界初始激励下极易振动,是大跨度索桥不可避免的问题,过大的振动幅度或过快的振动速率都会造成拉索吊索自身金属疲劳,力学性能降低,损伤累积的同时可能造成拉吊索断裂,造成桥梁垮塌,带来巨大经济损失以及严重威胁人的生命安全。因此,深入研究拉吊索的振动特性以及采取有效的抑制振动措施一直是各研究学者关注的关键问题。目前对于索桥中拉吊索的减振抑振措施大多采用3种减振措施:气动减振措施、阻尼器减振措施和辅助索(或者减振架)减振措施。围绕这其中的单个或者多个减振措施,国内外学者展开了一系列深入研究。

IRVINE[1]为分析均质悬索的自由振动,根据弦张力理论,建立了单根拉索在轴向力作用下的横向振动线性微分方程,在得出索的线性自由振动理论后又考虑拉索抗弯刚度的影响,深入讨论了索存在对称模态与反对称模态等一系列结论;PACHECO[2]在单索的基础上引进阻尼器,建立拉索-阻尼器系统的自由振动方程,采用Galerkin法进行求解,得出阻尼器的参数优化曲线;KRENK[3]也同样采用相似的拉索-阻尼器系统进行设计分析,运用复特征值法推导出了单索-阻尼器系统的复特征方程,用迭代方法求解了更为精确的解析解;AHMAD[4-5]在多根单索基础上引入辅助索,研究了多索索网系统以及多索索网-阻尼器系统等模型,根据弦理论建立了系统平衡方程并通过数值方式进行求解;CARACOGLIA[6-7]基于数值解析法求解了索网-阻尼器系统方程,并用实际桥梁进行了动力特性分析;冯立燕[8]通过理论分析和有限元分析相结合的方法研究了斜拉索-阻尼器索网系统的动力特性,分析其参数影响规律并对阻尼器的安装位置进行了参数优化;李明阳[9]进一步研究了带辅助索的多索索网系统以及多索索网-阻尼器系统等模型,研究分析了该系统的面内自振频率、阻尼比以及各阶振型的变化等规律;陈炜[10-11]在研究耦合索网系统的自振特性上考虑了斜拉索的抗弯刚度,求解更加符合拉索实际状态的特征方程;张卓杰[12]研究刚性耦合对多索股系统振动特性的影响,建立更加符合工程实际的模型;周海俊[13-15]建立了拉索-弹簧-阻尼系统模型,分析系统自由振动的频率及阻尼特性,指出在增设阻尼器的情况下可大幅度提高索网的阻尼;周现宝[16]和姚国灶[17]基于形状记忆合金辅助索材料建立了不同的阻尼器-双索系统模型,对系统的自振特性进行了分析,并通过试验进行验证;汪峰[18]建立了黏滞阻尼器-斜拉索-塔梁组合结构体系的参数振动耦合模型,分析了附加刚度对斜拉索固有频率的影响水平。

上述学者的研究结论有力地促进了拉吊索在减振抑振方面研究的发展,但无论是针对单索还是多索索网,其研究都是基于支座边界以及阻尼器安装在固定不动的桥面上这一假定的,而实际的阻尼器往往是锚固在易发生运动的桥面上,阻尼器的减振耗能作用会因桥面运动的存在而受到影响,已有减振模型不能合理反映这种现象。基于上述问题,罗帅[19-20]在单根斜拉索-阻尼器系统减振模型中合理考虑了桥面运动对拉索振动特性的影响;彭化义[21]推导了带TMD阻尼器的单根斜拉索减振系统分别在水平和竖向桥面运动下的平面内振动方程;曾智勇[22]同样建立单索-附加刚度阻尼器系统在桥面振动耦合下的平衡方程;尹娇霞[23]则是建立了单根斜拉索-TMD在端部轴向运动下面内振动的运动微分方程;姚志鹏[24]建立了考虑拉索弦向分力的斜拉索-桥面耦合参数振动模型,分析了系统频率比等因素对斜拉索-桥面耦合模型动力特性的影响。以上学者的研究均考虑了桥面运动这一因素的影响,考虑桥面边界运动与拉索-阻尼器系统的耦合作用,更加符合拉吊索在服役期间的真实运动状态。而在上述的研究中,未有学者对多索索网-阻尼器系统与桥面运动的耦合作用进行研究。

基于上述原因,研究并推导在桥面运动激励下多索索网-阻尼器系统的运动方程,通过设置不同辅助索刚度、辅助索位置、阻尼器位置、斜拉索倾角等因素研究桥面运动激励下索网-阻尼器系统的振动特性,同时得出桥面运动的最不利影响状态,所得结论对索网-阻尼器系统的设计及参数优化具有一定指导意义。

1 多索索网-阻尼器系统方程建立及求解

1.1 桥面运动下系统方程建立及求解

建立如图1所示的的n索索网-阻尼器系统模型,系统由n根不等长的平行斜拉索组成,斜拉索倾角为θ,其中上方最长斜拉索的长度为L1,往下斜拉索长度依次为L2至Ln;各斜拉索索力分别为T1至Tn;系统的拉索在振动过程中长度Li与索力Ti保持不变,即忽略拉索索力与索长增量,同时不考虑斜拉索的自身阻尼及抗弯刚度。拉索边界两端支座视为固定支座,上端支座共同锚固在桥塔一侧,下端支座共同固定于桥面上。拉索之间的辅助索用竖直的、具有一定刚度的轻质弹簧进行模拟,与平行斜拉索进行垂直连接,弹簧刚度分别为k1至kn-1,共计n-1根弹簧。每根斜拉索单独设置一个阻尼系数为ci的阻尼器,共计n个阻尼器,阻尼器一端垂直固定于斜拉索下端li1处,另一端与斜拉索下端共同锚固与桥面上,即发生桥面运动时,拉索、阻尼器与桥面共同运动。弹簧和阻尼器将每根拉索分为3个索段,即下部第一索段、中间第二索段、上部第三索段,则n根拉索共分为3n个索段,每个索段的长度分别为li1、li2、li3,每个索段之间可根据平衡条件联立求解。考虑后续求解方程组时将代入边界条件,为对计算进行简化,最上侧的n个索段l13、l23、l33、…、ln3以上端端点为坐标原点建立轴向坐标,其他索段以下端端部为原点建立轴向坐标,x方向为斜拉索轴向方向,坐标系等参数见图1。假定桥面发生微小振动时,斜拉索间继续保持平行,辅助索、阻尼器与斜拉索同样保持垂直。

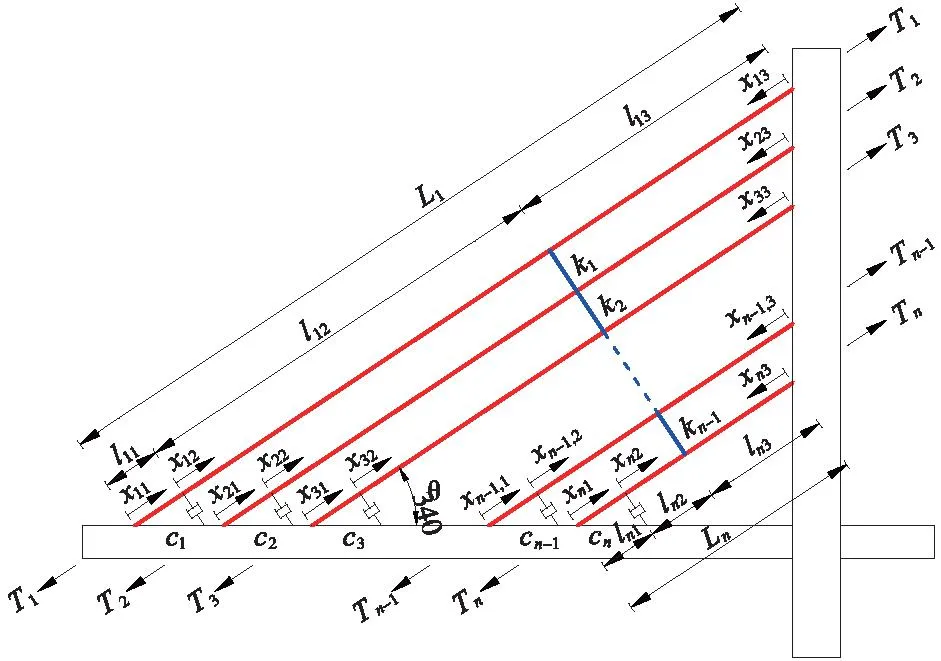
图1 n索索网-阻尼器系统模型Fig.1 Multi-cable network-damper system model

1.1.1 系统方程建立

不考虑自身阻尼及抗弯刚度条件下,图2所示的单根拉索在轴向拉力作用下的面内横向振动微分方程为[1]

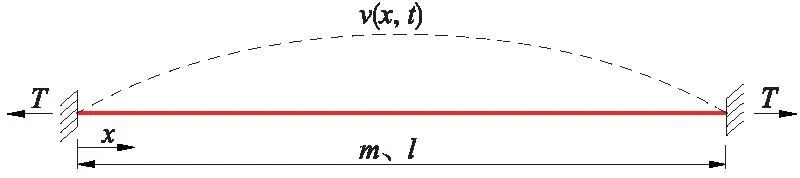
图2 单索振动模型Fig.2 Single cable vibration model

(1)

式中,v(x,t)为拉索横向位移;x为斜拉索横坐标;t为振动时间;T为拉索拉力;m为拉索单位长度质量,即线密度。

分析求解式(1),可采用变量分离法,设拉索自由振动方程的位移形式为

v(x,t)=φ(x)eIωt

(2)

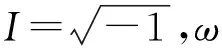
设竖向的桥面运动位移函数为

vg(t)=hgeIωgt

(3)

式中,hg为竖向桥面运动位移幅值;ωg为桥面运动频率。

把式(2)代入式(1),化简可得

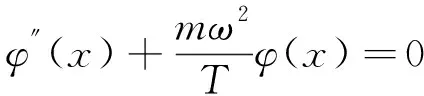
(4)

式(4)为二阶齐次线性常微分方程,其解为

φ(x)=Acos(αx)+Bsin(αx)

(5)

其中

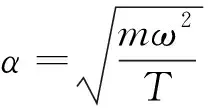
(6)

对于n索索网-阻尼器系统,各个索段振动方程的解形式如下

vij(xij,t)=φij(xij)eiωt=

[Aijcos(αixij)+Bijsin(αixij)]eIωt

(7)

式(7)中,i为拉索号,取值范围1～n,j为同一根拉索的索段号,取值为1、2、3;且

(8)

由于各索段通过耦合形成整体,故各索段的振动复频率相等,即

ωij=ω

(9)

因此,只需求解各索段的振型方程即可,则

φij(xij)=Aijcos(αixij)+Bijsin(αixij)

(10)

由于i取值范围1～n,j取值为1、2、3,且每个式(10)中包含有A、B两个未知参数,故式(10)为含有n×3×2=6n个未知待定系数的方程组。

1.1.2 系统方程求解

上述可知方程组有6n个未知待定系数,需要6n个平衡方程来求解,以下分别从边界条件、位移连续性条件、力平衡条件来确定平衡方程[9]。

(1)边界条件

由于斜拉索两端固结,拉索端部的振动位移为零,即

φi1(0)=φi3(0)=0

(11)

系统有n根拉索,故共计2n个方程。

(2)位移连续性条件1

同一拉索的第一、第二索段在阻尼器耦合点处的横向位移相等,并将该点位处的横向位移记为hdi,即

φi1(li1)=φi2(0)=hdi

(12)

系统有n根拉索,故共计n个方程。

(3)位移连续性条件2

同一拉索的第二、第三索段在辅助索耦合点处的横向位移相等,即

φi2(li2)=φi3(li3)

(13)

系统有n根拉索,故共计n个方程。

(4)位移连续性条件3

在第r根辅助索位置处,索网系统前r根拉索与第r+1根拉索在辅助索位置处的横向位移平衡条件为

φr+1,3(lr+1,3)-φr3(lr3)=

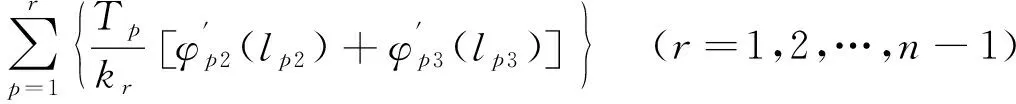
(14)

系统有n-1根辅助索,故共计n-1个方程。

(5)横向力平衡条件1

索网系统整体在辅助索耦合处的横向分力应满足以下平衡条件

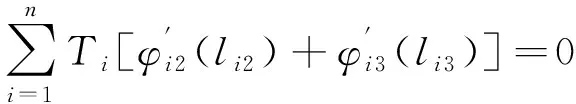
(15)

索网系统为一个整体,共计1个方程。

(6)横向力平衡条件2

如图3所示,桥面运动影响下,斜拉索-阻尼器-桥面间耦合运动,现分析三者间的平面几何关系。取如图4所示的某一斜拉索建立平衡方程,当桥面向上运动时,斜拉索下端边界由B运动到B′,位移大小为vgi,上文已设vgi(t)=hgieIωgit,C′D′与AB相交于F点,作辅助线BE垂直于AB′,由几何位移关系可知△AFD′∽△ABE,有|FD′|/|BE|=|AF|/|AB|,其中|BE|=|BB′|cosθ=vgicosθ,故由几何关系可得|FD′|=vgicosθ×(Li-li1)/Li,因此在计算阻尼力时应当减去由于阻尼器与桥面发生相对位移而产生的力。

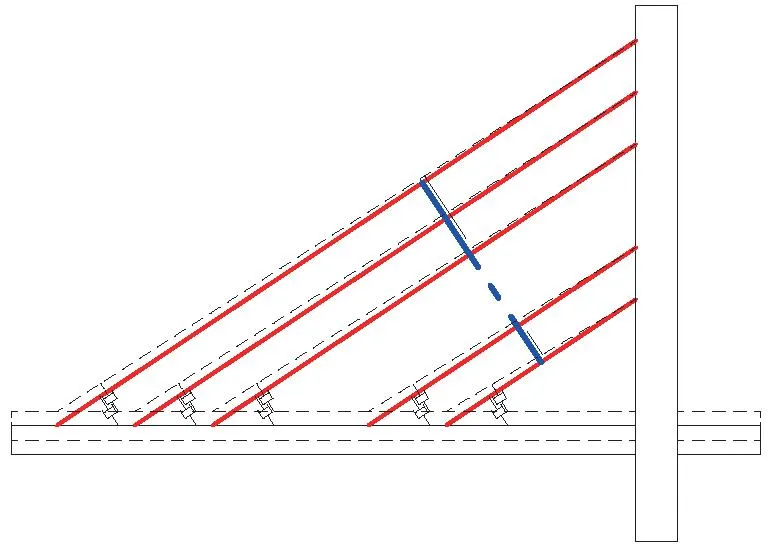
图3 桥面运动下n索索网-阻尼器系统模型(虚线为桥面运动)Fig.3 Multi-cable network-damper system under the bridge deck movement(The dashed lines represent the bridge deck movement)

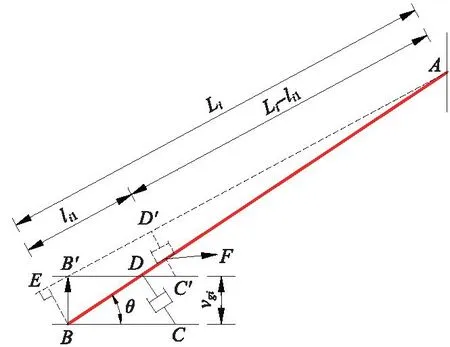
图4 桥面运动位移几何关系Fig.4 Displacement geometry relation of the bridge deck movement

在发生桥面运动后,单根斜拉索在阻尼器耦合点处的横向分力应满足的平衡条件为[15]

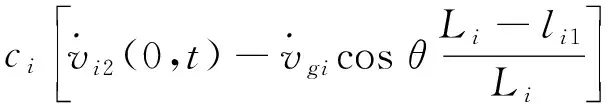
(16)

系统有n根拉索,故共计n个方程。

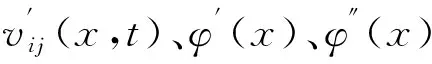
由平衡条件(1)～(6)可得6n个方程,可求解有6n个未知待定系数的索网系统方程组。

1.1.3 系统方程化简

为简便导出复特征方程以及进行参数分析,将定义以下参数对系统原参数进行无量纲化。

根据弦理论公式,对不考虑自身阻尼及抗弯刚度且完整性良好的柔性弦,其索力与频率的对应关系如下

T=4mL2f2

(17)

ω=2πf

(18)

令

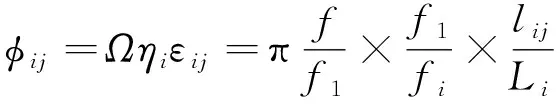
(19)

则有

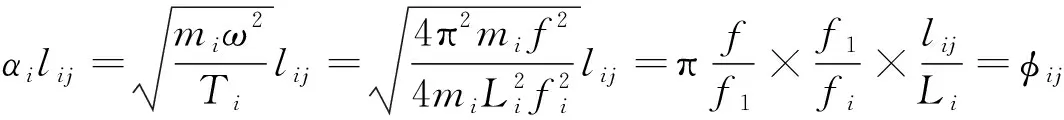
(20)

将式(11)～式(16)分别代入式(10)中,再结合上述无量纲参数,化简后可得

sin(φi1)Bi1-Ai2=0

(21)

cos(φi2)Ai2+sin(φi2)Bi2-sin(φi3)Bi3=0

(22)

sin(φr3)Br3-sin(φr+1,3)Br+1,3=0

(23)

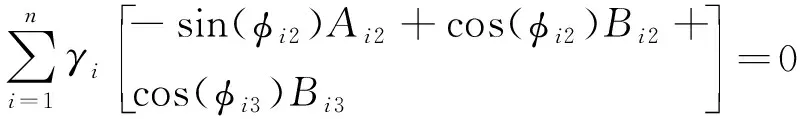
(24)

γicos(φi1)Bi1+IμiAi2-γiBi2=

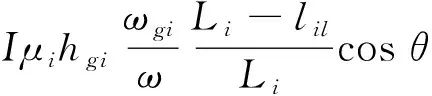
(25)

上述式(21)～式(25)是为不考虑自身阻尼及抗弯刚度的n索索网-阻尼器系统在桥面运动激励下的无量纲复特征方程组。此时注意到,由于边界条件的影响,方程组由原来的6n个方程变为4n个方程。但由于式(25)等号右端不为零,系统方程组为非齐次方程组,无法直接通过矩阵行列式求解,故对其进行化简。

在1.1.2节位移连续性条件1中已设阻尼器位置处拉索的横向运动幅值为hdi,即有Ai2=hdi。将式(25)右端的系数移至左端,有

γicos(φi1)Bi1-γiBi2+

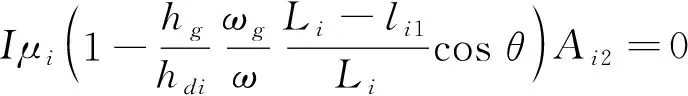
(26)

式(26)中,hgi/hdi为桥面运动幅值与阻尼器运动幅值之比;ωgi/ω为桥面运动频率与索网振动频率之比;(Li-li1)/Li为接地阻尼器位置与斜拉索索长之比。这里记Hi=hgi/hdi,Wi=ωgi/ω,Ldi=(Li-li1)/Li。

若令Hi=1,Wi=1,式(26)即变为

γicos(φi1)Bi1-γiBi2+

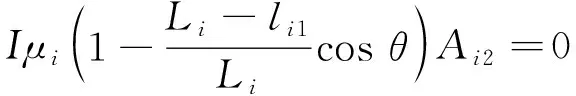
(27)

且当i=1时,即只有单根拉索和一个阻尼器发生桥面运动时,式(27)形式同文献[15-16]的形式一样。

将式(21)～式(24)及式(26)共计4n个方程写成矩阵形式

KX=0

(28)

K为4n×4n的系数矩阵,X为4n×1的待定系数列向量。其中

(29)

要使式(28)有解,系统复特征方程的系数矩阵行列式应为零,即

det(K)=0

(30)

由于上述方程为高次函数,可通过数学软件Wolfram Mathematica进行编程计算求解。方程中只有一个未知数ω,且ω为复数,可在复数域内使用牛顿迭代法(Newton-Raphson method)求得ω=α+Iβ的值,将已经求得的实部α与虚部β代入式(31)中求出系统的各阶模态阻尼比。

(31)

此外,根据f=α/(2π)可以得到索网-阻尼器系统的有阻尼振动频率。

1.2 未发生桥面运动时索网-阻尼器系统方程建立及求解

为对比有、无桥面运动对系统自振特性的影响,以下将建立无桥面运动时系统复特征方程组。

当系统未发生桥面运动时,即不考虑桥面运动对阻尼器阻尼力的影响,上述1.1节横向力平衡条件2应该重新建立平衡关系,式(16)、式(25)应改写为

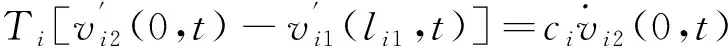
(32)

γicos(φi1)Bi1+IμiAi2-γiBi2=0

(33)

其余公式与上文推导过程一致,结合式(21)～式(24)及式(33)共4n个方程,即为索网系统在未发生桥面运动时的振动平衡方程,方程组共计有4n个未知参数Aij、Bij,方程可解,求解过程也同式(28)～式(31)一致。

2 有、无桥面运动时索网-阻尼器系统参数分析

2.1 两索索网-两阻尼器系统方程建立及求解

上文进行了桥面运动激励下n索索网-阻尼器系统方程组的建立以及化简求解,从方程组可看出,其求解结果受诸多因素影响。这些影响因数有:辅助索位置、辅助索刚度、阻尼器位置、斜拉索倾角、桥面运动幅值与阻尼器运动幅值之比、桥面运动频率与索网振动频率之比等。为分析以上因素对索网振动特性的影响,现建立桥面运动激励下两索索网-两阻尼器系统,如图5所示。

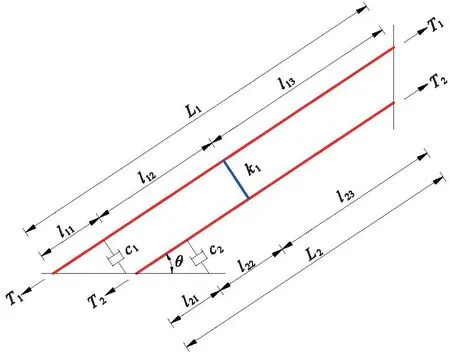
图5 两索索网-两阻尼器系统模型Fig.5 Two-cable network-two-damper system model

根据式(21)～式(24)及式(26),当拉索数i=2时,桥面运动下两索索网-两阻尼器系统的方程可写为

sin(φ11)B11-A12=0

(34)

sin(φ21)B21-A22=0

(35)

cos(φ12)A12+sin(φ12)B12-sin(φ13)B13=0 (36)

cos(φ22)A22+sin(φ22)B22-sin(φ23)B23=0 (37)

-γ1ψ1Ωsin(φ12)A12+γ1ψ1Ωcos(φ12)B12+

γ1ψ1Ωcos(φ13)B13+sin(φ13)B13-sin(φ23)B23=0

(38)

γ1[-sin(φ12)A12+cos(φ12)B12+cos(φ13)B13]+

γ2[-sin(φ22)A22+cos(φ22)B22+cos(φ23)B23]=0

(39)

γ1cos(φ11)B11-γ1B12+

Iμ1(1-H1W1Ld1cosθ)A12=0

(40)

γ2cos(φ21)B21-γ2B22+

Iμ2(1-H2W2Ld2cosθ)A22=0

(41)

将以上8个方程写成矩阵形式

KX=0

(42)

K为8×8的系数矩阵,X为8×1的待定系数列向量。其中

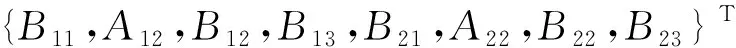
(43)

要使式(42)有解,系统复特征方程的系数矩阵行列式应为零,即

det(K)=0

(44)

化简后得到的桥面运动激励下两索索网-两阻尼器系统复特征方程如式(45)所示。

γ1μ1μ2sinφ11sin(φ12+φ13)sinφ21sinφ22sinφ23-

γ2μ1μ2sinφ11sinφ12sinφ13sinφ21sin(φ22+φ23)+

γ1γ2μ1μ2ψ1Ωsin(φ11)sin(φ12+φ13)sinφ21×

sin(φ22+φ23)+H1Ld1W1γ1μ1μ2cosθsinφ11×

sin(φ12+φ13)×sinφ21sinφ22sinφ23+

H1Ld1W1γ2μ1μ2cosθsinφ11sinφ12sinφ13sinφ21×

sin(φ22+φ23)+H2Ld2W2γ1μ1μ2cosθsinφ11×

sin(φ12+φ13)sinφ21sinφ22sinφ23+H2Ld2W2γ2μ1μ2×

cosθsinφ11sinφ12sinφ13sinφ21sin(φ22+φ23)+

H1Ld1W1γ1γ2μ1μ2ψ1Ωcosθsinφ11sin(φ12+φ13)×

sinφ21sin(φ22+φ23)+H2Ld2W2γ1γ2μ1μ2ψ1Ω×

cosθsinφ11sin(φ12+φ13)sinφ21×

sin(φ22+φ23)-H1H2Ld1Ld2W1W2γ1μ1μ2cos2θ×

sinφ11sin(φ12+φ13)sinφ21sinφ22sinφ23-

H1H2Ld1Ld2W1W2γ2μ1μ2cos2θsinφ11×

sinφ12sinφ13sinφ21sin(φ22+φ23)-

H1H2Ld1Ld2W1W2γ1γ2μ1μ2ψ1Ωcos2θsinφ11×

sin(φ12+φ13)sinφ21sin(φ22+φ23))+

sinφ13sin(φ21+φ22+φ23)+γ1γ2μ1sinφ11×

sin(φ12+φ13)sin(φ21+φ22)sin(φ23)+

γ1γ2μ2sin(φ11+φ12)sinφ13sinφ21×

sin(φ11+φ12+φ13)sinφ21sin(φ22+φ23)-

sinφ13sin(φ21+φ22+φ23)-H1Ld1W1γ1γ2μ1×

cosθsinφ11sin(φ12+φ13)sin(φ21+φ22)sinφ23-

sin(φ11+φ12+φ13)sinφ21sinφ22sinφ23-

H2Ld2W2γ1γ2μ2cosθsin(φ11+φ12)×

cos[θ]sin(φ11+φ12+φ13)sinφ21sin(φ22+φ23))=0

(45)

同理,在不考虑桥面运动时,式(40)、式(41)应改写为

γ1cos(φ11)B11+Iμ1A12-γ1B12=0

(46)

γ2cos(φ21)B21+Iμ2A22-γ2B22=0

(47)

结合式(34)～式(39)、式(46)、式(47),再经过式(42)～式(44)进行求解,就可得出未发生桥面运动时的两索索网-两阻尼器系统复特征方程。

2.2 各项因素对系统阻尼比的影响

在2.1节所求系统复特征方程的基础上,将分析该系统在上述诸多影响因素下的自振特性。首先先确定各参数的取值范围,见表1。

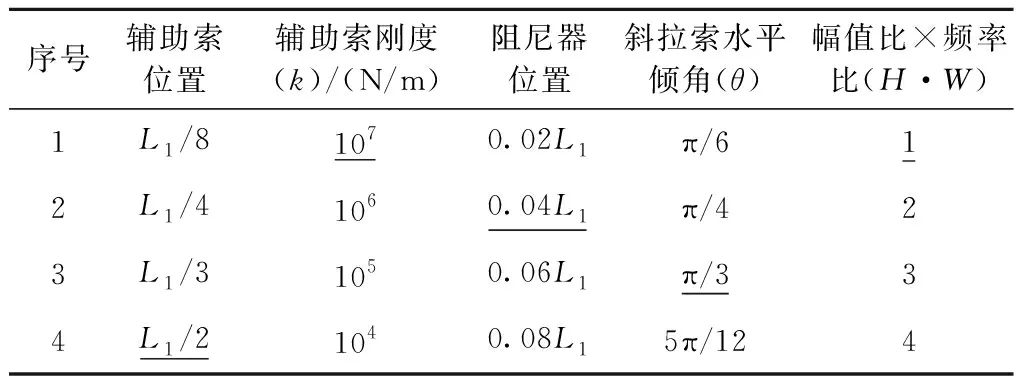
表1 各影响因素取值Tab.1 The value of each influencing factor

系统中两斜拉索相关参数如下。

1号索:L1=100 m,T1=3 500 kN,m1=60 kg/m,单索基频f1=1.208 Hz;

2号索:L2=96 m,T2=3 500 kN,m1=60 kg/m,单索基频f2=1.258 Hz。

2.2.1 辅助索位置对系统阻尼比的影响

为研究辅助索位置对系统阻尼比的影响,取表1中4个不同辅助索位置参数,其余因素保持固定参数不变,经式(45)计算,分别得出系统在发生桥面运动时的复频率ω实部α与虚部β的值,并根据式(31)求出系统的第1阶模态阻尼比,即可得出不同辅助索位置时系统第1阶模态阻尼比与阻尼系数的关系曲线(以下简称“关系曲线”),同理,系统在未发生桥面运动时的关系曲线也一并得出,如图6所示。由各关系曲线得出系统在不同辅助索位置下1阶最大(最优)阻尼比以及其对应的阻尼系数(以下简称“最优阻尼系数”),见表2。

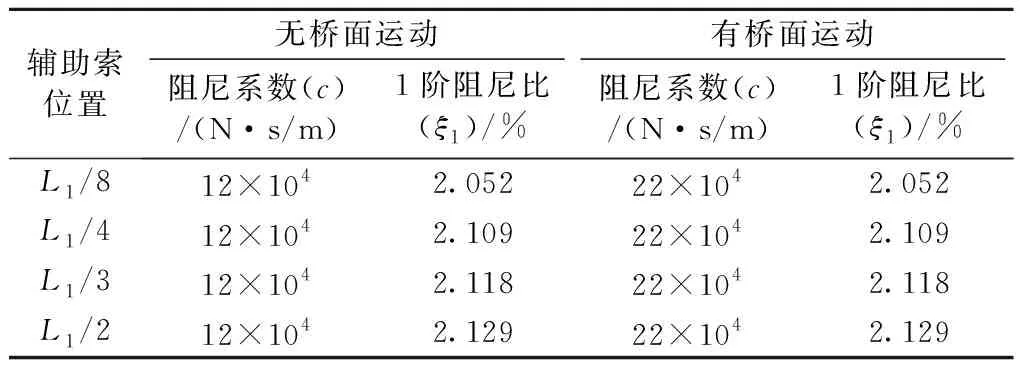
表2 不同辅助索位置下系统最优阻尼系数Tab.2 The optimal damping coefficient of the system under different cross-ties positions

图6 不同辅助索位置下系统关系曲线(实线表示桥面运动、虚线表示无桥面运动,下同)Fig.6 The system relationship curves under different cross-ties positions (The solid line represents the bridge deck movement, the dashed line represents no bridge deck movement, the same below)

由图6和表2可知,对于两索索网-阻尼器系统,对比有、无桥面运动两种工况,有桥面运动作用下,系统关系曲线的峰值相对于无桥面运动关系曲线的峰值往后移动,系统1阶模态最优阻尼系数从12×104N·s/m增至22×104N·s/m,说明桥面运动对系统自振特性影响很明显,即在考虑桥面运动作用下,需要为系统提供更大阻尼系数的外置阻尼器,才能使阻尼器起到相同的效果。

在辅助索位置度改变时,系统的关系曲线随之发生变化。辅助索的位置从L1/8移动至L1/2(即辅助索愈靠近拉索中部),关系曲线逐渐上移,在有、无桥面运动两种不同工况下,系统最优阻尼比均从2.052%增长至2.129%,变化幅度不明显,在图6中部分曲线近乎呈现重合状态,说明辅助索位置这一影响因素对系统最优阻尼比影响不大。值得注意的是,在辅助索位置相同时,有、无桥面运动这两种不同工况对应的系统1阶模态最优阻尼比是一致的。

2.2.2 辅助索刚度对系统阻尼比的影响

同样地,绘制有、无桥面运动时不同辅助索刚度下系统的关系曲线,如图7所示;各关系曲线的最优阻尼系数见表3。

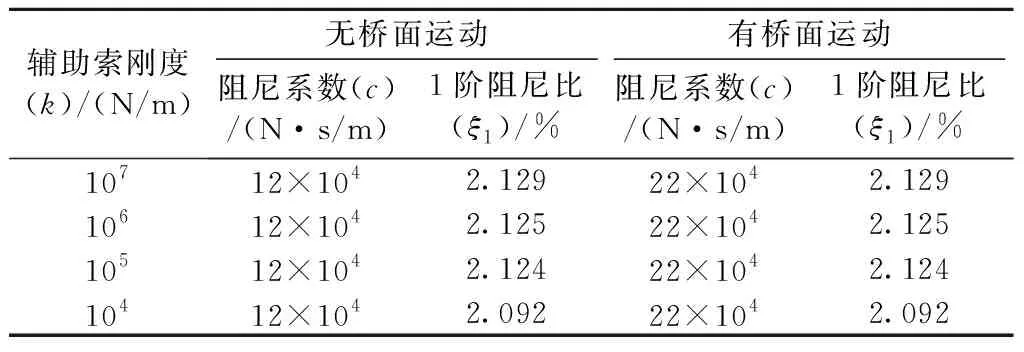
表3 不同辅助索刚度下系统的最优阻尼系数Tab.3 The optimal damping coefficient of the system under different cross-ties stiffness

图7 不同辅助索刚度下系统关系曲线Fig.7 The system relationship curves under different cross-ties stiffness

由图7和表3可知,当辅助索刚度从107N/m降低至104N/m时,关系曲线逐渐下移;在有、无桥面运动两种不同工况下,系统最优阻尼比均从2.129%降低至2.092%,变化幅度同样微小,曲线也近乎重合,说明辅助索刚度这一影响因素同样对系统最优阻尼比有影响,但影响不大。但值得注意的是,辅助索刚度相同时,有、无桥面运动这两种不同工况对应的系统1阶模态最优阻尼比是相同的;同样,有桥面运动作用下,关系曲线也相对于无桥面运动的曲线整体后移,系统1阶模态的最优阻尼系数从12×104N·s/m增至22×104N·s/m,上述规律与2.2.1节一致。

2.2.3 阻尼器位置对系统阻尼比的影响

考虑工程实际中接地阻尼器位置一般设置在斜拉索下端,且距离较接近锚固端,因此在分析阻尼器位置因素的影响时,其参数取值不宜过大。绘制系统在有、无桥面运动时的关系曲线,如图8所示,各关系曲线中最优阻尼系数见表4。

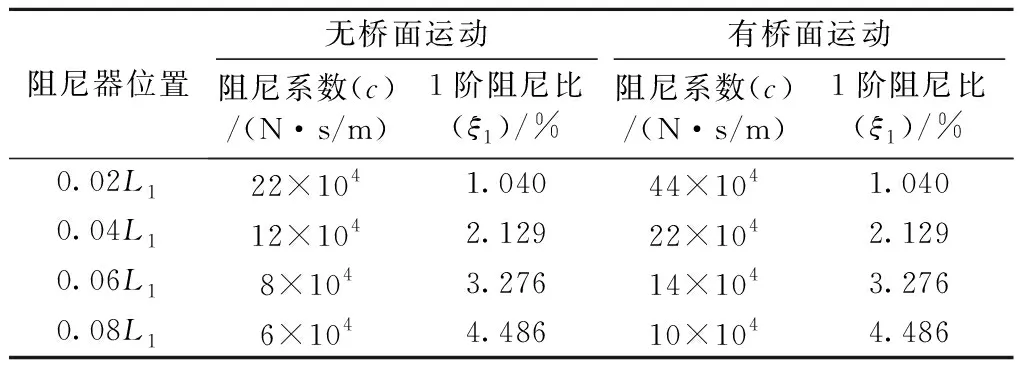
表4 不同阻尼器位置下系统最优阻尼系数Tab.4 The optimal damping coefficient of the system under different damper position

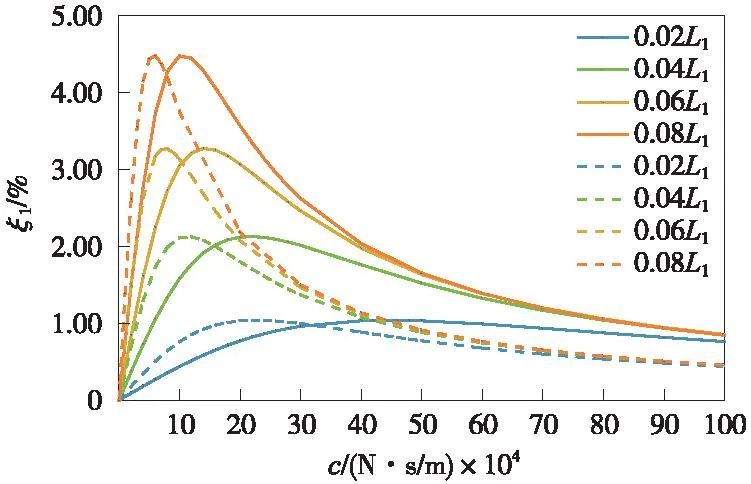
图8 不同阻尼器位置下系统关系曲线Fig.8 The system relationship curves under different damper position

由图8和表4可知,不论是有桥面运动还是无桥面运动,当阻尼器位置发生变化时,系统的1阶阻尼比与阻尼系数关系曲线均明显变化。在有桥面运动作用下,系统关系曲线相对于无桥面运动的曲线后移,与上文结论一致。

当系统未发生桥面运动,阻尼器位置从0.02L1移动至0.08L1时,系统关系曲线上移趋势明显,系统1阶最优阻尼比从1.040%增至4.486%,增长趋势接近倍数关系;同时最优阻尼比所对应的阻尼系数逐渐前移减小,从22×104N·s/m减低至6×104N·s/m,阻尼系数降低的同时还能提高系统1阶阻尼比,相当于起到双重作用,说明阻尼器位置这一因素对系统自振特性影响相对较大。同样地,系统发生桥面运动时,阻尼器位置从0.02L1移动至0.08L1时,系统1阶最优阻尼比也从1.040%增至4.486%;而阻尼系数从44×104N·s/m减低至10×104N·s/m。由此可见,阻尼器位置愈远离索端,对系统减振愈有利。

2.2.4 斜拉索倾角对系统阻尼比的影响

当考虑斜拉索倾角θ的影响时,上文式(46)、式(47)中未含有θ项,即未发生桥面运动时,斜拉索倾角对系统自振特性无影响。故此节仅讨论系统在发生桥面运动时的相关规律,幅值比×频率比(H·W)对系统阻尼比的影响也同样不考虑无桥面运动的影响。同时,当斜拉索倾角θ变化时,而L1与L2又保持不变,为保证斜拉索系统的平面几何关系,可通过调节两平行斜拉索之间的距离来满足。

同样地,绘制在桥面运动下不同斜拉索倾角时系统的关系曲线,如图9所示,各关系曲线中最优阻尼系数见表5。

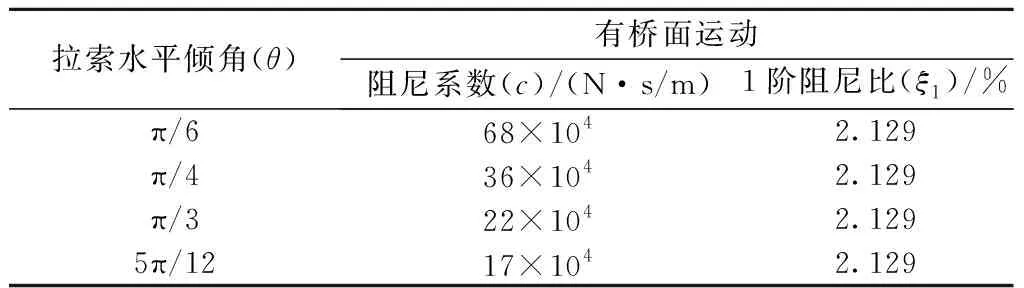
表5 不同斜拉索倾角下系统最优阻尼系数Tab.5 The optimal damping coefficient of the system under different inclination angle of the cable

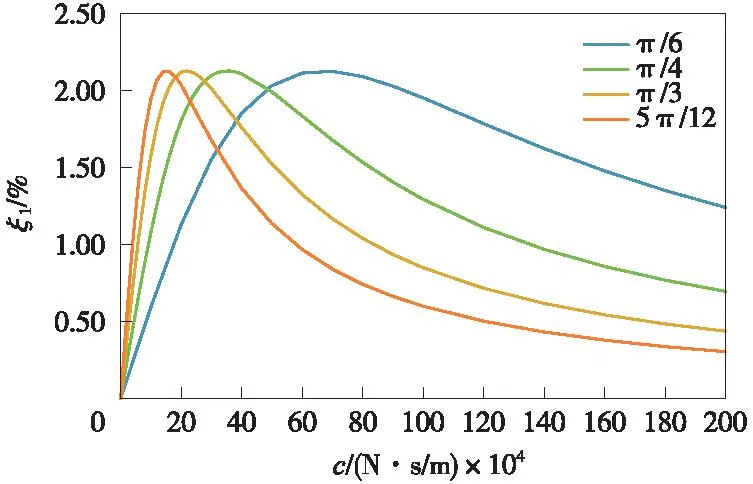
图9 不同斜拉索倾角下系统关系曲线Fig.9 The system relationship curves under different inclination angle of the cable

由图9和表5可知,在桥面运动工况下,斜拉索倾角θ发生变化时,系统的1阶阻尼比与阻尼系数关系曲线变化明显;当斜拉索倾角θ从π/6变化至5π/12时,系统关系曲线逐渐前移,阻尼系数从68×104N·s/m减低至17×104N·s/m,降幅显著,说明倾角对系统自振特性影响较大,但最优阻尼比均保持2.129%不变。由此可知,当斜拉索倾角愈大时,系统达到最优阻尼比所需要的阻尼愈小,对系统愈有利。

2.2.5 幅值比×频率比(H·W)对系统阻尼比的影响

同上述一样,绘制在桥面运动下不同H·W时系统的关系曲线,如图10所示,各关系曲线中最优阻尼系数见表6。

表6 不同H·W下系统1阶最优阻尼系数Tab.6 The optimal damping coefficient of the system under different the product of amplitude ratio and frequency ratio

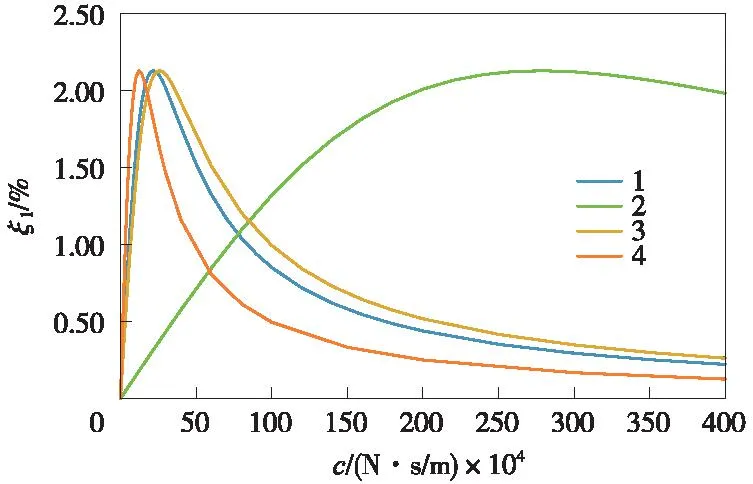
图10 不同H·W下系统关系曲线Fig.10 The system relationship curves under different the product of amplitude ratio and frequency ratio

由图10和表6可知,在桥面运动工况下,当H·W从1变化至4时,系统关系曲线变化明显,先往右移动而后向左移动,阻尼系数先从22×104N·s/m骤增至280×104N·s/m,后再骤降至12×104N·s/m,变化趋势较大,说明幅值比与频率比乘积的值对系统的自振特性影响很大,而最优阻尼比同上述一样均保持2.129%不变。

为更好地研究H·W的值与系统1阶模态最优阻尼比下阻尼系数之间的关系,从上文分析注意到,当1-H1W1Ld1cosθ=0时,系统处于最不利状态。通过变形得H1W1=1/(Ld1cosθ),此处阻尼器位置固定参数为0.04L1,斜拉索倾角θ固定参数为π/3,则有Ld1=(L1-0.04L1)/L1=0.96,cos(π/3)=0.5故H1W1=1/(0.96×0.5)=2.083,这里分为H1W1>2.083与H1W1<2.083两种情况来进行讨论。现将H·W从0～2.083,2.083～4这两个区间按0.01连续取值,计算求出系统1阶最优阻尼比所对应的阻尼系数,如图11所示。

图11 桥面运动下H·W与系统1阶模态最优阻尼系数关系曲线Fig.11 The relationship between the product of amplitude ratio and frequency ratio and the first-order mode optimal damping coefficient of the system under the bridge deck movement

从图11可看出,当H·W愈接近H1W1时,即H1W1Ldicosθ愈接近1时,系统与桥面运动接近共振,当桥面运动与系统达到共振时,即为系统的最不利影响状态。当H·W从两侧接近2.083时,最优阻尼比对应的阻尼系数迅速增大,即系统需要更大的阻尼系数才能达到相同的最优阻尼比;当H·W=H1W1时,计算出阻尼系数接近无穷大,而在实际工程中不存在阻尼系数无穷大的阻尼器。工程中斜拉索的外置阻尼器的阻尼系数一般为固定数值,在发生桥面运动时,阻尼器起到的耗能作用相对减小,接近或达到共振时,阻尼器对系统减振耗能起不利效果,近乎失去减振效果。因此,在设计系统的减振措施时,应避开两者的共振区。

2.3 桥面运动对系统自振频率的影响

为研究系统在有、无桥面运动时,不同阻尼系数对系统自振频率的影响,根据方程分别计算出系统的前10阶模态频率,方程中固定参数选项同表1一致,自振频率计算数值具体如表7、表8所示,图12、图13分别为其变化曲线。

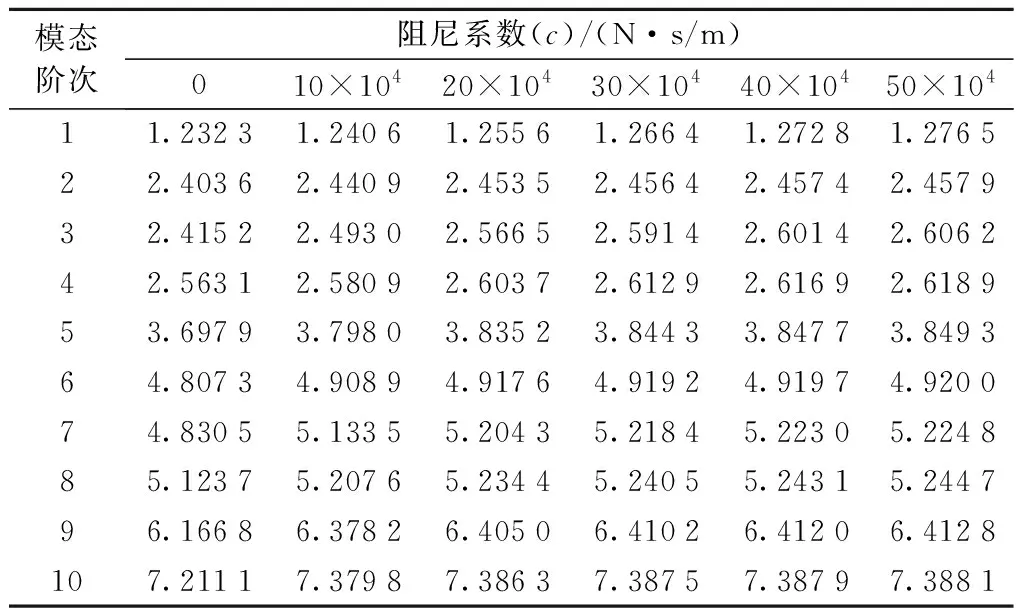
表7 桥面运动时系统在不同阻尼系数下前10阶频率Tab.7 The first 10 frequencies of the system under different damping coefficients when the bridge deck is moving

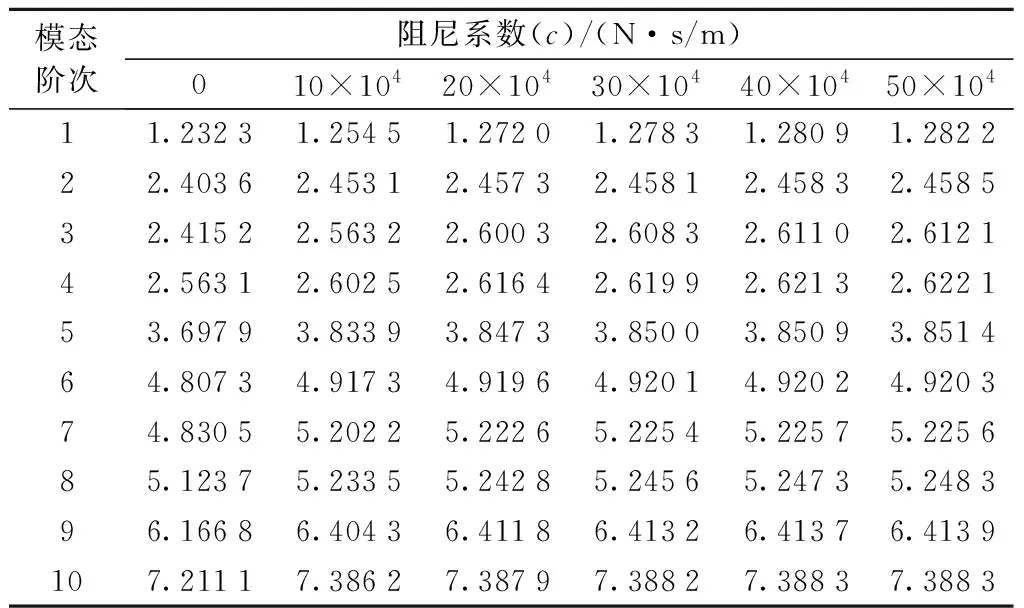
表8 无桥面运动时系统在不同阻尼下前10阶频率Tab.8 The first 10 frequencies of the system under different damping coefficients without bridge deck motion

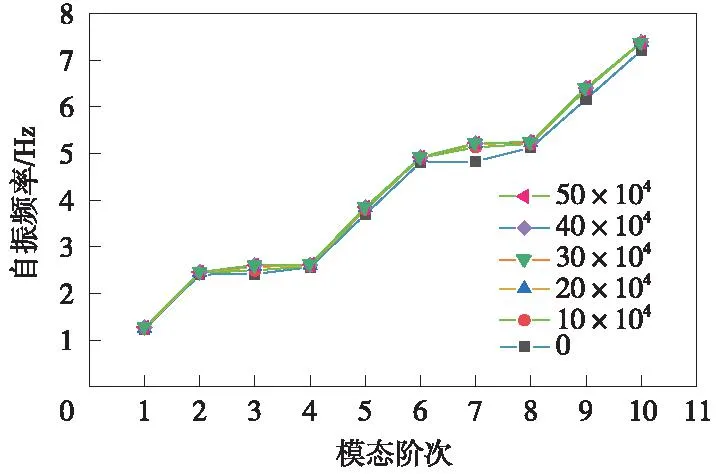
图12 桥面运动时系统在不同阻尼系数下前10阶频率变化曲线Fig.12 The first 10 frequencies change curve of the system under different damping coefficients when the bridge deck is moving

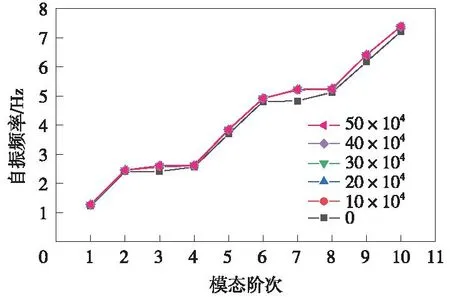
图13 无桥面运动时系统在不同阻尼系数下前10阶频率变化曲线Fig.13 The first 10 frequencies change curve of the system under different damping coefficients without bridge deck motion

从表7、表8与图12、图13可以看出,不论是有桥面运动还是无桥面运动,随着阻尼系数增加,系统各阶频率均有不同程度增长。有桥面运动时,频率最大增幅为8.164%,发生在第7阶,而最小增幅也有2.178%,出现在第4阶;在无桥面运动时,频率最大增幅同样发生在第7阶,达8.164%,而最小增幅则出现于第2阶,为2.282%,说明阻尼系数对系统自振频率有一定影响。对比表7与表8,发生桥面运动后,系统在同一阻尼系数下,各阶自振频率均有不同程度增长,但总体增幅较小,说明发生桥面运动后对系统自振频率的影响不大,其中最大涨幅仅为2.817%,出现在阻尼系数为10×104N·s/m的第3阶,而其余各阶次频率变化幅值在1%以内。

3 结论

以不考虑自身阻尼及抗弯刚度的n索索网-阻尼器系统为研究对象,建立并求解该系统在桥面运动激励下的复特征方程组。然后对两索索网-阻尼器系统进行了参数分析,研究结论如下。

(1)在分析索网-阻尼器系统的自振特性时,应该考虑桥面运动与系统的耦合作用,桥面运动激励对索网-阻尼器系统的自振特性产生显著影响。

(2)桥面运动时,系统关系曲线相对于无桥面运动的曲线后移,对系统产生不利影响。

(3)发生桥面运动时,索网的辅助索位置愈远离拉索中部、辅助索刚度愈小、阻尼器位置愈靠近边界、斜拉索倾角愈小、HW的值愈接近H1W1时,桥面运动对系统的影响愈不利,反之则有利。

(4)当1-H1W1Ld1cosθ愈接近0时,系统与桥面运动愈接近共振,当桥面运动与系统达到共振时,阻尼器近乎失去减振耗能效果,此时即为系统的最不利影响状态。

(5)有、无桥面运动时,系统各阶频率均随着阻尼系数的增大而增大;而发生桥面运动后系统的自振频率相对于无桥面运动时的变化则减小。