毕达哥拉斯犹豫模糊集多属性决策研究
关 欣, 刘 赢
(海军航空大学, 山东 烟台 264000)
0 引 言
在模糊信息的多属性决策问题中,众多学者一直致力于模糊集[1]的改进和推广。其中,针对模糊集仅考虑隶属度这一缺陷,Atanassov提出的直觉模糊集(intuitionistic fuzzy set, IFS)[2],通过增加非隶属度和犹豫度的概念,对模糊集进行了拓展,使其能够更完整地描述模糊信息。但IFS的隶属度与非隶属度的和不超过1的约束条件在实际应用时常常不能够满足,使得IFS存在诸多应用场景的限制。在此基础上,Yager等提出了毕达哥拉斯模糊集(Pythagorean fuzzy set, PFS)[3-4],使其能描述隶属度和非隶属度之和超过1,而平方和不超过1的模糊现象, 拓展了应用范围。PFS虽然改善了IFS的约束条件,但其本质上仍无法对群体决策中专家的不同评价进行合理的描述。为此,在犹豫模糊集[5]的基础上,刘卫锋等[6]给出了毕达哥拉斯犹豫模糊集(Pythagorean hesitation fuzzy set, PHFS)的相关定义,其约束条件与毕达哥拉斯模糊集一致,描述方法与犹豫模糊集类似,是PFS的一种有效的改进形式。
自PHFS提出以来,众多学者已经取得了丰富的研究成果。其中,刘卫锋等[7]定义了PHFS的信息能量、相关指标以及相关系数,并对其性质进行了证明。Wei等[8-10]研究了一系列PHFS平均算子与集成算子。Liang等[11]对毕达哥拉斯犹豫模糊数(Pythagorean hesitation fuzzy element, PHFE)的距离测度进行了研究分析,并应用于多属性决策问题。常娟等[12]在传统PHFE距离测度基础上,提出了广义PHFS混合加权距离测度。与文献[6]中所提出的PHFS不同,Muhammad等[13]也提出了一种PHFS,可以理解为IFS在PFS环境中的一种推广。Wu等[14]提出了多种形式的PHFS距离测度,并在毕达哥拉斯模糊环境下,提出了一种扩展多准则妥协解排序法(vise kriterijumski optimizacioni racun, VIKOR)的多属性群决策方法。Akram[15-16]又先后将消去与选择转换法(elimination and choice translating reality, ELECTRE)-II和ELECTRE-I方法应用于毕达哥拉斯犹豫模糊环境下的多属性决策问题,如风险评估、电子商务决策方案评估以及人力资源设施安全评估等。
可见,PHFS的理论成果已日趋丰富,但上述研究多偏重多属性决策应用,对PHFS基本性质的改进涉及较少,尤其是得分函数、距离测度以及规范化方法等,如现有得分函数[6]存在某些特殊情形下可能会失效的情况。现有PHFE距离测度要求集合中的元素个数相等,需要进行规范化处理,而现有规范化方法多根据某种风险规则重复添加数值最大或者最小的元素[7,15-16],这改变了原本的数据信息,造成了人为误差的引入,因此对得分函数以及规范化方法的进一步研究是十分必要的。
常见的多属性决策方法有逼近理想解排序法(technique for order preference by similarity to ideal solution, TOPSIS)方法[11]、VIKOR方法[17]以及交互式多准则决策(interative multi-criteria decision-making, TODIM)方法[18],其中TOPSIS方法以及VIKOR方法是建立在决策者完全理性的前提下。而在实际应用中,参与决策的人员往往会表现出有限理性的心理特征行为,如对收益和损失的偏好不同等等,因此需要采用更符合决策思维习惯的决策方法。目前的主流方法是结合前景理论的特点,对传统决策方法进行拓展[19-21]。与之相比,TODIM方法本身便基于前景理论考虑决策者心理行为,且无需事先确定参考点,通过引入一个多准则值函数来计算各个方案的优势度,该函数考虑每个决策者的损失偏好,相比传统VIKOR与TOPSIS方法,评估更加客观和准确。
但传统TODIM方法多是假定属性间相互独立,现有毕达哥拉斯犹豫模糊环境下的多属性决策研究[11-16]也多是在属性间相互独立的前提下进行的。而在现实决策中,由于问题的复杂性以及决策者认知的局限性,属性间往往是相互关联的,属性间的关联关系会对决策结果产生重大影响。Choquet积分[22]与模糊测度为属性间具有相互关联关系的决策问题提供了强有力的工具。相关学者在其基础上,已经探讨了区间模糊集[23]以及犹豫模糊集[24]等环境下属性关联的多属性决策问题,因此研究毕达哥拉斯犹豫模糊环境下属性关联的多属性决策问题是十分必要的。
基于以上,本文的主要工作总结如下:① 针对现有得分函数存在的问题, 考虑PHFE的犹豫度,并结合从众心理,提出了一种新的得分函数;② 针对现有PHFS规范化方法人为引入误差等不足,提出一种最小公倍数规范化原则;③ 针对属性关联的多属性决策问题,基于λ-模糊测度和Choquet积分,改进了传统TODIM方法,并推广至毕达哥拉斯犹豫模糊环境中。
文章首先介绍了PHFS的基本概念,其次分析了现有的得分函数以及规范化方法的缺陷,随后基于从众心理提出了改进的得分函数与最小公倍数规范化原则,然后基于λ-模糊测度和Choquet积分对TODIM方法进行拓展,并结合改进的得分函数与距离测度,提出了改进的TODIM多属性决策方法,最后通过实例分析验证了本文算法的有效性。
1 相关概念
本节主要介绍PHFS及距离测度的相关概念。
1.1 PHFS
为方便起见,下文将PHFE记为α=〈Γα,Ψα〉。
关于PHFE的犹豫度的定义,不同文献之间存在一定的争议,如刘卫锋、Muhammad等[6-7,12-13]将犹豫度以集合的形式表示:
(1)
而Liang、Akram等[11,15-16]则与精确函数相联系,将犹豫度定义为
(2)
由于犹豫度表征的是决策者不确定的程度,而隶属度与非隶属度均为决策者所确定的信息,精确函数表征的也是决策者的确定信息。因此,本文倾向于采用式(2)的定义,即犹豫度应与精确函数相关联,相比式(1)既有更为明确的物理意义,也减少了计算量。
1.2 PHFE距离测度
文献[13]结合隶属度和非隶属度给出了一种PHFE间的距离测度,具体定义如下。
给定PHFEα=〈Γα,Ψα〉和β=〈Γβ,Ψβ〉,假设各集合元素基数均相等,即k1=|ΓΘ|,k2=|ΨΘ|,Θ={α,β}。则PHFEα和β的距离定义为
d1(α,β)=
(3)
式中:σ(i)表示集合中第i大的元素。
在此基础上,文献[11]通过添加犹豫度,定义了一种改进的PHFE距离测度,具体定义如下。
给定两PHFEα=〈Γα,Ψα〉和β=〈Γβ,Ψβ〉,假设各集合元素基数均相等,则PHFEα和β的距离定义为
(4)
式中:犹豫度πα、πβ根据式(2)计算求得。
2 改进PHFE得分函数
2.1 现有得分函数分析
假设α=〈Γα,Ψα〉为一PHFE,刘卫峰等[6]将PHFE的得分函数定义为
(5)
式中:|Γa|,|Ψa|分别表示Γα,Ψα中的元素基数,且sa∈[-1,1],sa数值越大,则α越大。
并且根据得分函数定义了如下比较法则:
设α=〈Γα,Ψα〉,β=〈Γβ,Ψβ〉,有
(1) 若sa>sβ,则a>β;
(2) 若sa=sβ,则a=β;
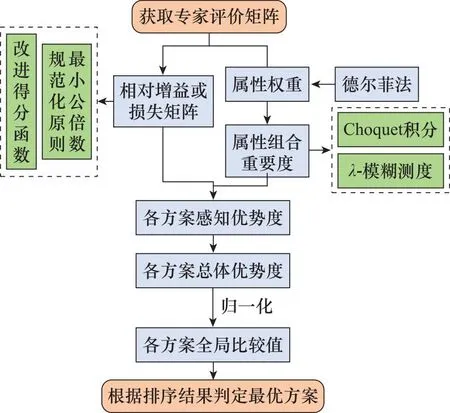
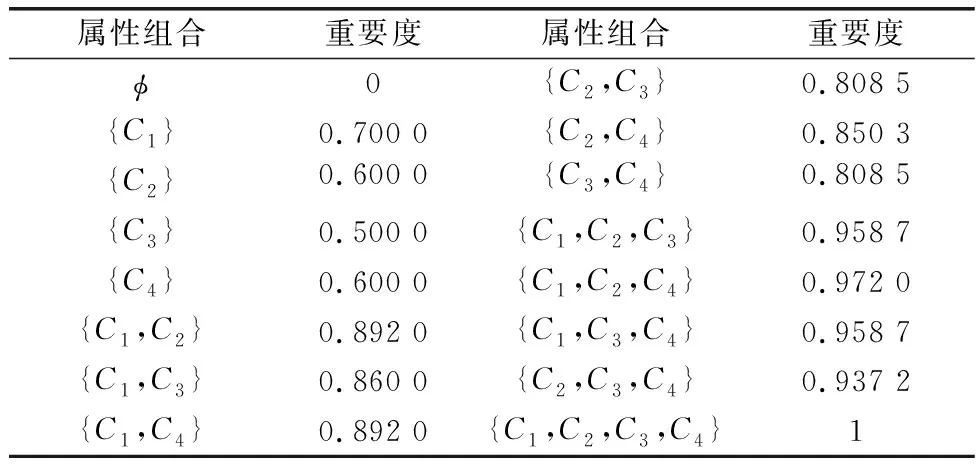
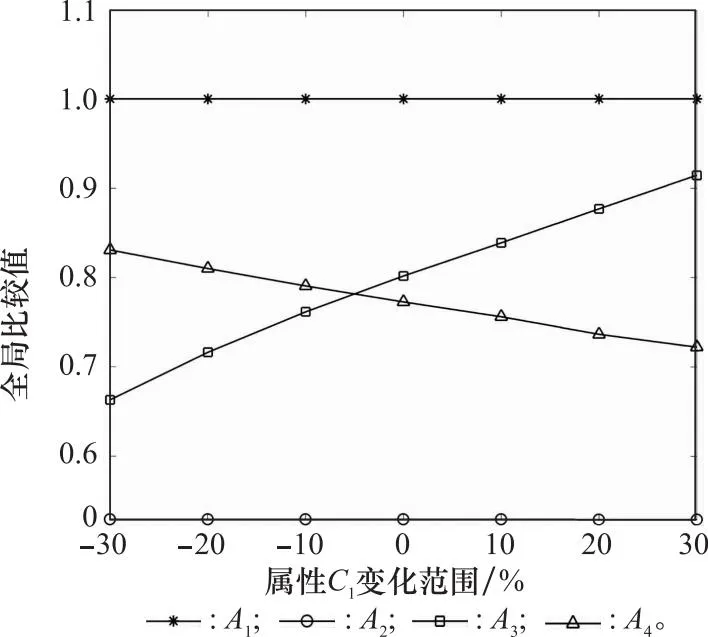
(3) 若sa 为此,Liang等[11]定义了PHFE的精确函数,假设α=〈Γα,Ψα〉为一个PHFE,则α的精确函数定义为 (6) 分析上述得分函数与精确函数,二者主要存在以下缺陷:① 仅仅通过得分函数,并不能很好地处理PHFE的比较问题,尽管随着精确函数的提出这一情况得到了改善,但同时也增加了计算成本;② 现有得分函数与精确函数都是对隶属度与非隶属度进行分析,没有将犹豫度纳入计算中,从而没有完全利用PHFE包含的信息,这在一定程度上导致了信息的损失。 基于以上,本文将提出一种改进的得分函数。 文献[25]引入了从众心理的概念,该理论表明犹豫中的决策者并不完全中立,其会受到隶属度和非隶属度的影响,当隶属度大于非隶属度时,犹豫中的决策者会倾向于偏向支持,对得分函数起到正向作用;当隶属度小于非隶属度时,犹豫中的决策者会倾向于偏向反对,并反向作用于得分函数。同时,决策者总是希望最优方案中的支持度越高, 反对度越低,犹豫度(即不确定性)越低越好。因此,本节基于从众心理这一思想,通过考虑犹豫度对决策的影响,提出一种改进的得分函数,具体定义如下。 定义 1假设α=〈Γα,Ψα〉为一PHFE,其中lα=|Γa|,mα=|Ψa|,分别表示集合Γα,Ψα的元素基数,新的得分函数定义为 (7) 深入分析本文新的得分函数,给出以下若干定理。 证毕 定理 2假设α=〈Γα,Ψα〉为一PHFE,其得分函数满足: (1)spro(α)∈[-2,2]; (2) 当且仅当α=[{1},{0},0]时,有spro(α)=2;当且仅当α=[{0},{1},0]时,有spro(α)=-2。 证明由定理1中得分函数的单调性可知, 证毕 证毕 定理1说明了隶属度越大,得分函数越大,非隶属度越大,得分函数越小;定理2根据其单调性分析了其取值边界。定理1~定理3描述了新得分函数所具有的性质,证明其不仅保留了文献[6]中得分函数具有的优势,还弥补了未考虑犹豫度所带来的不足。 分析表明,当无法区分两PHFE的大小时,相比文献[6]的得分函数,需要通过计算精确函数才能得出比较结果,本节所提出的得分函数可以直接得出比较结果,不需要二次比较,在一定程度上简化了计算过程。 由第1.2节分析可知,现有PHFE距离测度均要求隶属度和非隶属度集合的元素个数一致,为了便于PHFE间的比较,文献[7,15-16]等给出了一种规范化方法,具体步骤如下。 (1) 当γ=1时,补充元素分别为μ+和v+,此时,决策者为乐观决策者; (2) 当γ=0.5时,补充元素分别为(μ++μ-)/2和(v++v-)/2,此时决策者为中立决策者; (3) 当γ=0时,补充元素分别为μ-和v-,此时决策者为悲观决策者。 下面通过一个例子对规范化过程进行说明。 例1假设α1=[{0.4,0.5,0.54},{0.7,0.8}]和α2=[{0.45,0.5},{0.55,0.67,0.78}]为两PHFE,其规范化后的结果如下: 根据式(5)和式(6)计算上述规范化后的PHFE的得分函数与精确函数。分析可知,上述规范化过程改变了PHFE原本的数据信息,人为地引入了误差,从而影响最终的决策结果,因此需要对现有的规范化方法进行改进。 由于现有的规范化方法在决策者偏好参数的影响下容易引入人为误差,本节在文献[26]的启发下,提出一种最小公倍数拓展(least common multiple expansion, LCME)规范化方法。 定义 2假设α=〈Γ,Ψ〉为一PHFE,其中隶属度集合Γ={μ1,μ2,…,μl}的元素个数为l,则定义Γ的r倍集合为Γr: (8) 即Γ中的元素重复次数为r,非隶属度的处理方法同样,此处不再赘述。 定义 3假设α=〈Γ,Ψ〉为一PHFE,其中,隶属度集合Γ={μ1,μ2,…,μl}的元素个数为l,非隶属度集合Ψ={v1,v2,…,vm}的元素个数为m,则定义αr1,r2为 αr1,r2=<Γr1,Ψr2>= (9) 即规范化后的PHFEαr1,r2中隶属度集合中元素重复次数为r1,非隶属度集合中元素的重复次数为r2,LCME规范化原则的关键就在于重复次数r1和r2的确定,实际规范化的实现过程通过以下例子进行说明。 例2假设α1=〈{0.4,0.5,0.6},{0.3,0.4}〉和α2=〈{0.2,0.3},{0.4,0.5,0.6,0.7}〉为两PHFE,则α1中隶属度集合元素个数为3,非隶属度集合元素个数为2,α2中隶属度集合元素个数为2,非隶属度集合元素个数为4。容易得到,α1与α2隶属度集合元素个数的最小公倍数为6,非隶属度集合元素个数的最小公倍数为4。因此,α1的隶属度集合中各元素需重复2次,非隶属度集合中各元素需重复3次,α2的隶属度集合中各元素需重复2次,非隶属度集合中各元素需重复1次。最终得到规范化后的结果如下: α1=〈{0.4,0.4,0.5,0.5,0.6,0.6},{0.3,0.3,0.4,0.4}〉 α2=〈{0.2,0.2,0.2,0.3,0.3,0.3},{0.4,0.5,0.6,0.7}〉 下面给出LCME规范化方法的性质不变定理。 定理 4假设α和αr1,r2分别为一PHFE及其对应的规范化PHFE,则其得分函数相等。 根据式(8)中本文得分函数的定义可知: spro(αr1,r2) 证毕 定理4表明,利用LCME原理,PHFE的得分函数保持不变,对应的隶属度与非隶属度集合的均值保持不变,相应的PHFE之间的相对大小也保持不变。换言之,PHFE可以保持信息质量,根据LCME原则规范化后不会丢失数据原本的信息。 因此,本文定义PHFE之间的距离测度为在LCME规范化原则的基础上,根据式(4)的距离测度方法进行求解。 本节针对属性关联条件下的PHFS多属性决策问题,基于λ-模糊测度与Choquet积分,在改进得分函数与LCME规范化原则的基础上,提出一种改进的TODIM方法。 设论域为X={x1,x2,…,xn},P(X)为X上的幂集,则X上的模糊测度[27]定义为一个集合函数μ:P(X)→[0,1],其中μ应满足以下两个公理性条件: (1)μ(φ)=0,μ(X)=0; (2) ∀A,B∈P(X),如果A⊆B,则μ(A)≤μ(B)。 其中,λ-模糊测度为一类特殊的模糊测度,其满足以下附加条件[28]: μ(A∪B)=μ(A)+μ(B)+λμ(A)μ(B) 其中,对于∀A,B∈P(X)且A∩B∈φ,λ满足-1≤λ≤∞。 λ-模糊测度常用于描述集合之间的相互关系。当λ=0时,μ(A∪B)=μ(A)+μ(B),A、B之间不存在相互作用;当λ∈(-1,0)时,μ(A∪B)<μ(A)+μ(B),A、B之间存在冗余关系;当λ>0时,μ(A∪B)>μ(A)+μ(B),A、B之间存在互补作用。 (10) 式中:xi∩xj=φ,i,j=1,2,…,n,且i≠j。 λ的数值可以由μ(X)=1唯一确定,即式(10)可以变形为 (11) Choquet积分是一种对模糊数据进行非线性集结的工具,允许测度交互作用的存在。 设f为论域X={x1,x2,…,xn}上的非负函数,μ为论域X上的一模糊测度,则X上关于μ的离散Choquet积分[29]定义为 CIμ(f(x1),f(x2)…f(xn))= (12) 式中:σ(i)表示第i大的排列顺序;f(xσ(i))满足0≤f(xσ(1))≤f(xσ(2))≤…≤f(xσ(n)),且Aσ(j)={xσ(j),xσ(j+1)…xσ(n)},Aσ(n+1)=φ,f(xσ(0))=0。 假设有M个备选方案X={x1,x2,…,xM},N种属性C={c1,c2,…,cN},现有一组专家对备选方案进行评估,由于专家存在不一致的情况,评估结果采用PHFE的形式表示。假设属性不是相互独立的,即属性间相互关联。采用λ-模糊测度和Choquet积分进行属性之间的交互建模,具体步骤如下。 令本文问题中属性集的权重向量为W=[ω1,ω2,…,ωN]T=[μ(c1),μ(c2),…,μ(cN)]T。其中,ωj=μ(cj)表征属性cj的权重,满足0<μ(cj)<1。根据第4.1节的描述,对于属性cj、cp,j,p∈N,可能存在以下3种关系。 (1) 无相互关系:μ(cj∪cp)=μ(cj)+μ(cp); (2) 冗余关系:μ(cj∪cp)<μ(cj)+μ(cp); (3) 互补关系:μ(cj∪cp)>μ(cj)+μ(cp)。 则改进的TODIM方法的决策步骤具体描述如下。 步骤 1获取PHFE决策矩阵A=[αij]M×N,其中αij表示备选方案xi在属性cj下的PHFE评估值。 步骤 2根据德尔菲法,邀请专家进行评估,得到属性权重W=[ω1,ω2,…,ωN]T。 (13) 步骤 4计算属性组合的重要度。 容易分析得到,属性集C={c1,c2,…,cN}共有2N种属性组合集,通过λ-模糊测度来表示属性组合的重要程度。设U为任意属性组合,μ(U)为U的重要度。计算U的重要度,需要首先确定参数λ: (14) 则计算得到属性组合U的重要度如下: (15) 式中:P(C)为C上的幂集。 步骤 5计算各方案的感知优势度。 并根据μ(Uσ(j))-μ(Uσ(j+1))计算得到属性cj的加性权重,其中μ(Uσ(j))表示属性组合Uσ(j)的重要度,Uσ(j)={cσ(j),cσ(j+1),…,cσ(N)}。 分别计算备选方案xi相对于xk的正、负感知优势度φ(xi,xk)-和φ(xi,xk)+: 式中:θ为衰退损失参数,θ越小,表明决策者规避损失的可能性越大。 则xi相对于xk的感知优势度φ(xi,xk)为 φ(xi,xk)=φ(xi,xk)-+φ(xi,xk)+ (18) 步骤 6计算各方案的总体优势度。 (19) 步骤 7归一化总体优势度,得到各方案的全局比较值。 (20) 步骤 8根据全局比较值对各方案进行排序,判定全局比较值最大的方案为最优方案。 则改进TODIM方法具体流程如图1所示。 图1 方法应用流程框架Fig.1 Method application process framework 为了便于比较,本文采用文献[12]中的算例进行仿真分析。 近年来,电商业务得到迅猛发展,物流在其中扮演着十分重要的角色,并承担着较高的支出比例,因此电商业务的发展好坏与物流公司关系紧密。现有某公司因电商业务拓展,需要从{A1,A2,A3,A4}4个备选物流公司中选出合适的公司。各领域专家分别从经营现状C1、电子化程度C2、设备质量C3、管理水平C4这4个方面进行评估。评估信息用PHFE表示。如每位专家分别用[0,1]区间上的数字对公司A2设备质量C3的满意度和不满意度进行评估。由于不同专家受教育水平与专业领域不同,因此存在不一致的意见,得到最终的满意度为0.3和0.4,不满意度为0.7和0.8,即A2在C3下的评估信息表示为α23=〈{0.3,0.4},{0.7,0.8}〉。类似地,可以确定其他评估值αij,具体评估信息如表1所示。 表1 PHFE评估信息矩阵Table 1 PHFE evaluation information matrix 步骤 1获取PHFE决策矩阵A=[αij]M×N如表1所示。 步骤 2根据德尔菲法,邀请多名专家进行打分,得到属性权重为W=[0.7,0.6,0.5,0.6]T。 步骤 4计算属性组合的重要度。 首先确定参数λ,计算公式如下: λ+1=(1+0.7λ)(1+0.6λ)(1+0.5λ)(1+0.6λ), -1<λ<∞;λ≠0 计算得到λ=-0.971 5。 根据以上计算各属性组合U的重要度,计算结果如表2所示。 表2 属性组合的重要度Table 2 Importance of each attribute combination 步骤 5计算各方案的感知优势度。 令衰退损失参数θ=1,根据式(16)~式(19)计算方案的感知优势度矩阵,可得 步骤 6计算各方案的总体优势度。 步骤 7归一化总体优势度,得到各方案的全局比较值。 步骤 8根据全局比较值对各方案进行排序,得到A1>A3>A4>A2,判定方案A1为最优方案。 判决结果与文献[12]中采用广义混合加权距离测度的结果一致,证明了本文算法的有效性。 (1) 衰退损失参数θ敏感性分析 衰退损失参数体现了决策者规避损失的心理偏好,其取值会对决策结果产生影响,因此有必要对其敏感性进行分析。设置θ不断递增,分别取值0.5,1,2,…,10,计算各方案的全局比较值变化情况,计算结果如图2所示。 图2 全局比较值随衰退损失参数θ的变化图Fig.2 Graph of global comparison value changing with decay loss parameter θ 由图2可知,随着衰退损失参数不断增大,各方案的排序结果有所不同:① 当0.5≤θ≤4时,排序结果均为A1>A3>A4>A2,当θ>4时,排序结果为A1>A3>A4>A2,θ的取值对排序结果产生了影响;② 随着θ的增大,方案A4的全局比较值增幅最为明显,表明决策者越倾向于接受风险,A4的总体优势度就越大,在实际决策中,就越容易得到决策者的认同;③ 在所有排序中,A1始终为最优选择,A2始终为最差选择,这与表1中A1、A2各属性值得分函数的整体情况一致。 分析表明本文算法对衰退损失参数具有一定的敏感性,在实际应用中,需根据决策者风险偏好及决策需求确定衰退损失参数的取值。 (2) 属性权重敏感性分析 本节对属性权重进行敏感性分析。首先,将第5.1节中的权重作为参考权重。在此基础上,各属性权重分别降低30%、20%、10%,以及提高10%、20%、30%。计算不同属性权重下各方案的全局比较值,计算结果如图3~图6所示。 图3 全局比较值随属性C1的变化图Fig.3 Graph of global comparison value changing with attribute C1 图4 全局比较值随属性C2的变化图Fig.4 Graph of global comparison value changing with attribute C2 图5 全局比较值随属性C3的变化图Fig.5 Graph of global comparison value changing with attribute C3 图6 全局比较值随属性C4的变化图Fig.6 Graph of global comparison value changing with attribute C4 图3~图6分别为全局比较值随4种属性权重的变化情况。分析可知:随着C1权重不断增大,A3的全局比较值逐渐增大,A4的全局比较值逐渐减小,当属性值变化范围为参考权重的-5%时,排序情况由A1>A4>A3>A2变为A1>A3>A4>A2;随着C2权重不断增大,整体的变化趋势与C1类似,此处不再赘述;随着C3权重不断增大,A4的全局比较值逐渐增大,A3的全局比较值逐渐减小,当属性值变化范围为参考权重的+5%时,排序情况由A1>A3>A4>A2变为A1>A4>A3>A2;随着C4权重不断增大,各方案始终保持A1>A3>A4>A2的排序结果,且A3、A4的全局比较值呈现逐渐减小的趋势,两者的差距也在不断缩小。 由上述分析可知,各方案整体的排序结果是一致的,即A1、A2始终为最佳和最差选择,仅A3、A4的相对优势度会随着权重的变化而有所不同,这验证了本文扩展TODIM方法的合理性,且具有良好的稳定性。 为了反映本文所提算法的有效性,本节将其与传统TODIM方法和TOPSIS方法进行比较。传统TODIM和TOPSIS方法中,属性间是相互独立的,不存在关联关系,属性权重采用熵权法[12]计算得到,TOPSIS方法中分别采用加权距离测度DPHFWA、有序加权距离测度DPHFOWA和混合加权距离测度DGPHFHWA(λ=0.2)3种测度进行计算,比较结果如表3所示。由表3可知,除采用DPHFWA距离测度方法外,大部分方法都表明方案A1为最佳选择,这验证了本文算法的有效性和可靠性。然而,本文改进的TODIM方法与TOPSIS方法的结论仍然存在一定的差异,如采用DPHFWA测度的TOPSIS方法判定A3为最佳方案,方案A1的排名仅优于方案A2,采用DPHFOWA测度的TOPSIS方法判定方案A4>A3。其原因有两点,一是该方法假设决策过程是绝对理性的,未能考虑决策者的有限理性行为,二是该方法未考虑属性间的相互关联问题。与传统的TODIM方法相比,虽然最终的判决结果整体上相同,但传统的TODIM方法仍然存在不足,虽然二者都考虑了决策模型的风险偏好,但传统TODIM方法并未考虑属性间的关联问题,本文的改进算法通过λ-模糊测度与Choquet积分很好地解决了这一问题。 表3 不同决策方法的结果对比Table 3 Comparison of different decision-making methods result 本文研究了属性关联下PHFS的多属性决策问题,主要贡献如下:① 针对现有得分函数存在的缺陷,将犹豫度纳入计算中来,提出一种改进的得分函数,同时证明了其相关定理与性质;② 针对距离测度要求元素个数相等,而现有规范化方法容易引入误差的缺点,提出一种最小公倍数规范化方法,保留了模糊数据原有的信息;③ 基于λ-模糊测度与Choquet积分,对传统TODIM方法进行拓展,提出一种改进TODIM决策方法,既解决了属性关联的问题,又通过前景理论将决策者的心理行为特征反映了出来,克服了现有大多数方法忽略决策者主观价值感受的缺陷。下一步将重点研究如何在不进行规范化处理的前提下,计算PHFE间的距离,以及如何更科学合理地确定属性权重。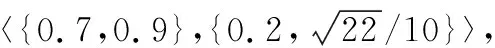
2.2 改进的得分函数

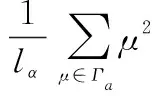


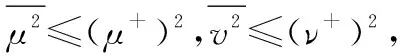


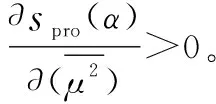


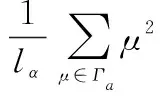
3 最小公倍数拓展规范化原则
3.1 现有规范化方法
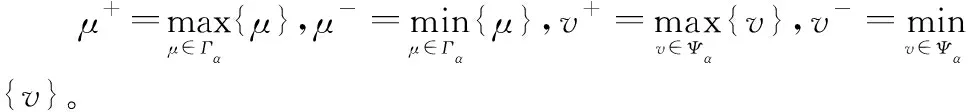



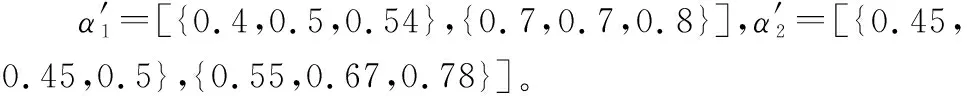
3.2 最小公倍数拓展规范化原则
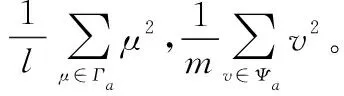

4 属性关联下的改进TODIM方法
4.1 λ-模糊测度和Choquet积分

4.2 改进的TODIM方法

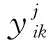
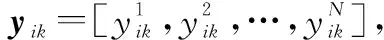
5 算例分析
5.1 应用计算


5.2 敏感性分析




5.3 不同算法比较分析

6 结束语

