基于视觉反馈的机械臂位置模糊控制

解霄鹏，王佳玮，高波，于凌涛

1. 哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001

2. 中国航空工业集团公司 哈尔滨空气动力研究所，黑龙江 哈尔滨 150009

机械臂的位置控制是机械臂控制领域的重要组成部分，合理的工作轨迹能够提高效率，降低能耗，因此研究机械臂的位置控制具有重要意义[1]。传统的位置控制方法需要获取机械臂的准确尺寸，建立运动学模型，进行笛卡尔空间规划或关节空间规划，计算量较大[2]。并且传统方法很难用于对柔性机械臂的控制，因为柔性机械臂的振动大大提高了建模复杂程度，需要融合多种智能算法进行深入的数学分析，很难实现误差补偿[3-4]。如今，利用视觉反馈技术的机械臂在实际生活中有了大规模的应用[5]。视觉传感器因具有精确性高、易用性强、获取信息完备以及信号范围广等特点，被用于许多场景[6]。本文将针对传统机械臂位置控制方法的不足，结合视觉反馈技术，提出一种机械臂位置的模糊控制方法，以解决传统方法受尺寸约束的问题，并初步用于柔性机械臂的研究。

1 总体方案设计

本文研究的机械臂具有3 个自由度，均为转动关节。第1 个转动关节在xoy平面内运动；第2 个转动关节和第3 个转动关节共面，在xoz平面内运动。如图1 所示，视觉传感器1 布置在机械臂上方，捕捉xoy平面信息，视觉传感器2 布置在机械臂前方，捕捉xoz平面信息，包括各个转动关节的坐标、机械臂末端的坐标、目标物的坐标。

图1 机械臂示意

在得到上述信息后，采用设计好的运动方向判断算法，即可得到各个转动关节的运动方向，让机械臂末端逐步靠近目标物体。在机械臂运动过程中，各个关节的运动速度通过模糊控制方法搭建二维模糊控制器进行求解。将上述2 种方法结合即可实现对机械臂的位置控制，完成对目标物的抓取。设计好核心算法后，在机器人操作系统（robot operating system，ROS）中建立机械臂模型，联合MATLAB 进行仿真实验验证，系统整体架构如图2 所示。

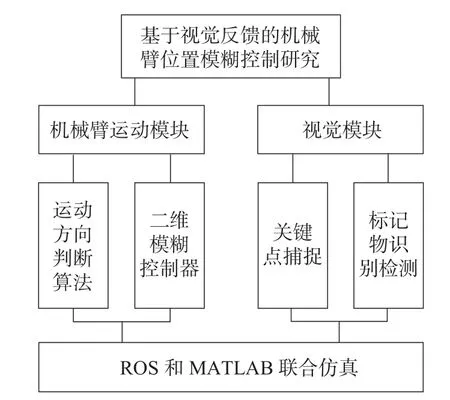
图2 系统整体架构

2 运动方向判断算法设计

在进行机械臂运动方向判断时，要调用视觉传感器得到机械臂的3 个关节、机械臂末端及目标物体分别在xoy和xoz平面的坐标，如表1 所示。

表1 通过视觉传感器得到的坐标

2.1 xoy 平面运动方向判断

在xoy平面，如果机械臂末端与目标物不重合，可以通过部分关键点坐标对关节1 和关节2 的运动方向进行判断。首先判断该平面机械臂末端到目标物的距离是否为0，如果dm45为0 则关节1 不转动，如果dm45不为0 则依据S1的正负判断关节2 的转向：S1＞0时关节2 逆时针转动，S1＜0时关节2 顺时针转动。

判断流程如图3 所示，规定逆时针方向为关节转动的正方向，ri值代表3 个关节的旋转方向，ri=0代表关节不转动，ri=1代表关节逆时针转动，ri=-1代表关节顺时针转动。

图3 xoy 平面运动方向判断流程

2.2 xoz 平面运动方向判断

2.2.1 关节1 和关节2 运动方向判断在2.1 节中已通过关键点坐标对关节1 和关节2 的运动方向做出初步判断。如果在xoz平面上机械臂末端与目标物不重合，其运动方向仍需进一步分析，并且对关节3 的运动方向进行判断。如图4 所示，在xoz平面上，判断该平面机械臂末端到目标物的距离是否为0，如果为0 则关节2 和关节3 不转动，如果不为0 则通过S2和S3判断关节1 和关节2 的转向。

当S2＞0时关节1 逆时针转动，当S2＜0时关节1顺时针转动；当S3＞0时关节2 逆时针转动，当S3＜0时关节2 顺时针转动。判断流程如图5 所示。

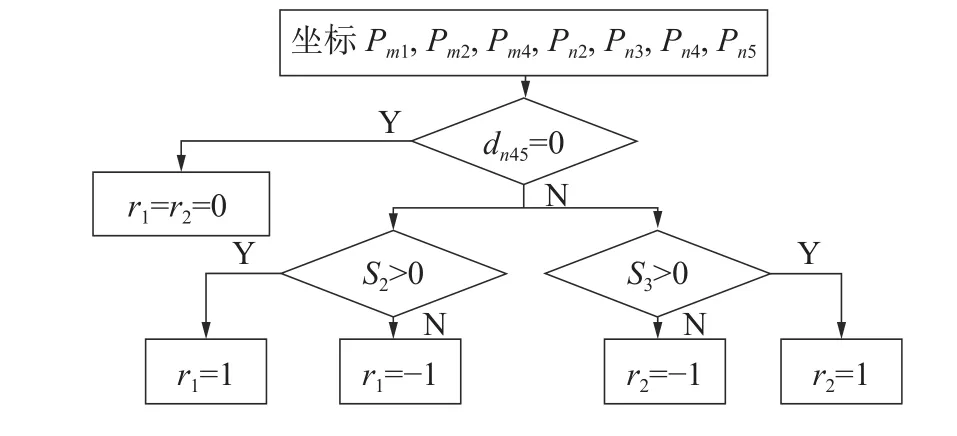
图5 关节1、2 在xoz 平面运动方向判断流程

2.2.2 关节3 运动方向判断

对于关节3 转动方向的判断，首先要用获得的坐标求出关节2 和机械臂末端之间的距离dn24、关节2 和目标物之间的距离dn25，再根据dn24和dn25的大小进行判断。如果两者相等，则关节3 不转动；如果两者大小不等，则进一步根据目标物和关节2 在xoz平面上的坐标yn2和yn5的大小进行判断。如果yn5≥yn2且dn24＞dn25，关节3 顺时针转动，反之关节3 逆时针转动；如果yn5＜yn2且dn24＞dn25，关节3 逆时针转动，反之关节3 顺指针转动。关节3 判断流程如图6 所示。

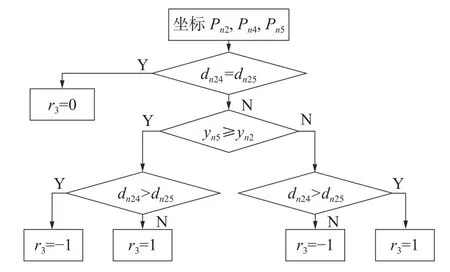
图6 关节3 在xoz 平面运动方向判断流程

3 模糊控制系统设计

模糊控制以模糊数学为基本理论，主要利用模糊推理技术进行控制[7]，是一种高效的非线性控制[8]。它可用于模型参数不确定或者波动较大的线性和非线性系统的控制[9-10]。本文采用模糊控制方法对机械臂速度进行控制。当末端距离目标物较远时，控制各关节以较大的速度运动；随着末端逼近目标物，速度逐渐减小。根据以上思路利用模糊控制工具箱，设定参数，完成模糊控制系统的设计。

3.1 输入量和输出量确定

常见的模糊控制器有一维模糊控制器和二维模糊控制器[11]。一维模糊控制器以偏差e作为输入量，二维模糊控制器以偏差e、偏差变化率ec作为输入量。二维模糊控制器与一维模糊控制器相比，虽然结构较为复杂，但是动态性能更好[12]，因此本文选用二维模糊控制器。

将机械臂的末端与目标物中心距离d以及其偏差变化率dc作为输入量；电机转速n为输出量，输出量个数为3，对应各关节的转速。输入量的计算需要获取机械臂的末端坐标Pi(xi,yi)和目标物坐标P(x,y)，di为距离偏差，dci为偏差变化率，采样时间间隔为 Δt，则：

3.2 模糊化

在确定输入量和输出量后，首先完成隶属度函数的确定。综合考虑整个系统的精度和运算效率，将三角形隶属度函数和高斯型隶属度函数相结合[13]，接着确定各个变量的模糊论域空间。把d、dc、n的基本论域设置为[0,xd]、[-xdc,xdc]、 [0,yn]，对模糊空间进行分割[14]。随着分割级数的增多，系统的精度也会提高，但是会使系统结构更加复杂。采用试凑的方法，先将分割级数设置为7 级，后续可根据精度要求进行调整。D、DC、N与d、dc、n对应，是输入量和输出量的模糊语言变量。D的模糊子集为{EJ, BJ, LJ, ZO, LY, BY, EY}，论域为{0,1,2,3,4,5,6}；DC的模糊子集为{NB, NM,NS, ZO, PS, PM, PB}，论域为{-3,-2,-1,0,1,2,3}；N的模糊子集为{ES,FS,BS,ZH,BB,FB,EB}，论域为{0,0.5,1,1.5,2,2.5,3}。设置量化因子kd=6/xd、比例因子kn=yn/3，为了保证系统精度，量化因子取值范围设置如下：

式中δ为允许的控制误差。

比例因子kn影响系统的快速性和稳定性，kn越大，系统的快速性越好，但是如果kn过大会出现超调，稳定性下降，因此在模糊控制器结构上加入参数调整器调整kn的大小。参数调整器的输入量为d，Kn与kn对应，Kn的模糊子集为{ES, FS, BS,ZH, BB, FB, EB}，论域为{0, 0.5, 1, 1.5, 2, 2.5, 3}，最终确立的模糊控制系统结构如图7 所示。

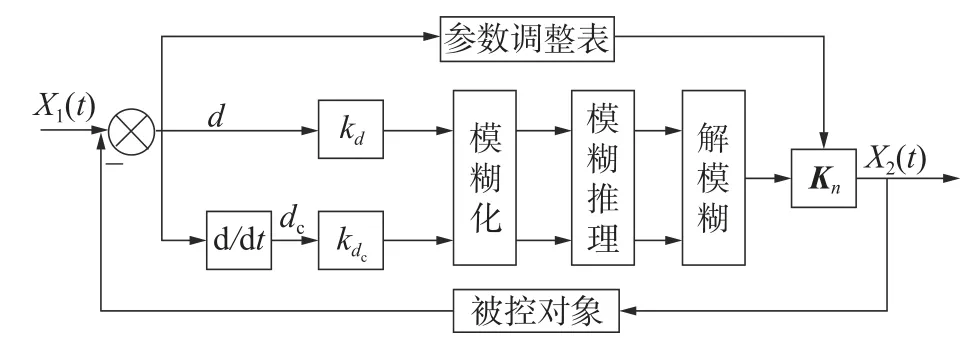
图7 模糊控制系统结构

3.3 模糊规则确定

首先确定基本模糊控制器的模糊规则。基本模糊控制器的输入量为d和dc，文中将分割级数设置为7 级，则模糊规则库包含49 个形式为“ifthen”的模糊条件语句，它们决定了模糊关系Ri=(A×B)T×C，由49 个模糊规则经过运算后可得49 个模糊关系矩阵，对它们求并可得到最终的模糊关系矩阵R。输入量的模糊集合为D和DC，模糊推理过程为U=(D×DC)T·R，即可得到对应控制量的模糊集合。控制输出量的模糊规则如表2 所示，模糊规则为“ifDis EJ andDCis NB thenNis ES”。

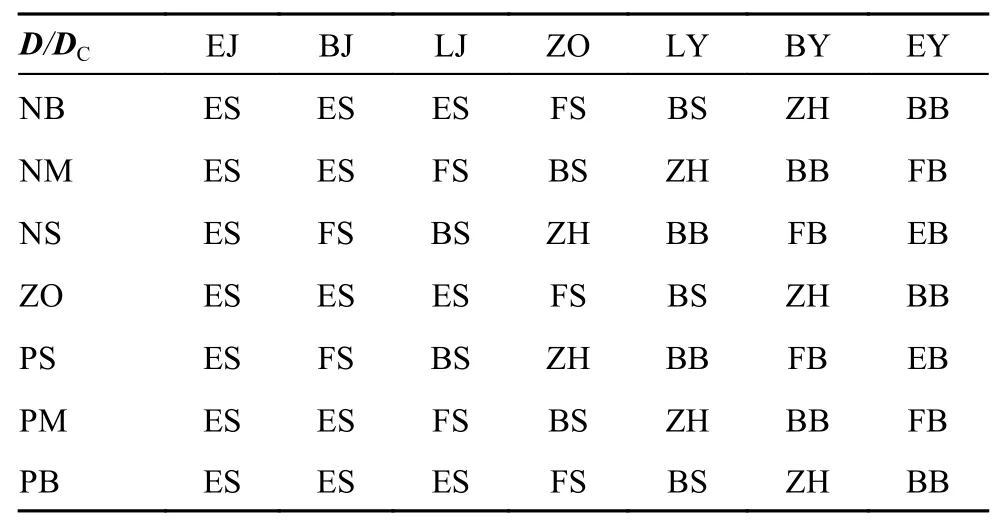
表2 基本模糊控制器模糊规则表

接着确定参数调整器的模糊规则。参数调整器输入量只有d，因此有7 个形式为“if-then”的模糊条件语句。在初始阶段为了加快系统响应速度，将比例因子kn设置成一个较大的值，以此来提高控制能力。当d较大时增大kn，让系统的输出趋向稳态；当d减小时，也要逐步减小kn的值，使系统具有较好的稳定性。控制输出量的模糊规则如表3 所示。

表3 参数调整器模糊规则表

3.4 解模糊化

完成上述运算后，输出量以模糊语言的形式表示，通过解模糊化可以将模糊输出值映射到真实世界。采用面积重心法对基本模糊控制器和参数调整器进行解模糊化操作，它的输出值是隶属度函数图与坐标轴构成的图像的重心[15]。这种方法的特点是在进行输出过程中控制值更加平滑，即使输入信号存在很小的变化，输出信号也能够跟着变化。面积重心法表达式为

式中：V为输出论域，v为输出论域中的值，µv(v)为隶属度函数，v0为模糊推理输出。

离散域的表达式为

式中：vi为离散域下输出论域中的值，µv(vi)为隶属度函数，v0为模糊推理输出，n为输出量化级数。

对输出量进行解模糊化即完成了整个模糊控制系统的设计。搭建完模糊控制系统后，通过对控制结果的观察、调整模糊规则和隶属度函数等，对系统性能进行改善。

通过视觉传感器获得机械臂的末端和目标物的坐标，计算2 点的距离，并通过求解其偏差变化率作为模糊控制器的输入量，调用模糊控制器，计算系统的输出，得到其对应输出量，就可以实现对各个关节运动速度的控制。再结合文中的运动方向判断算法，即可完成对机械臂的位置控制。

4 机械臂位置控制仿真分析

4.1 仿真系统建立

仿真系统整体框架如图8 所示，在Gazebo 中搭建机械臂的三维模型，建立三维仿真环境，用以检验机械臂的控制算法效果。ROS 采用话题、服务、Action 作为基本的通信手段，采集节点信息传输给MATLAB。MATLAB 会对视觉传感器的图像进行处理，进行目标识别，获取关键点坐标。在获取了3 个关节、末端、目标物体在空间内的坐标后，利用运动方向判断算法判断机械臂的运动方向，通过模糊控制工具箱，将各个关节的速度信息反馈给ROS，控制机械臂三维模型进行运动，实现对机械臂的位置控制。

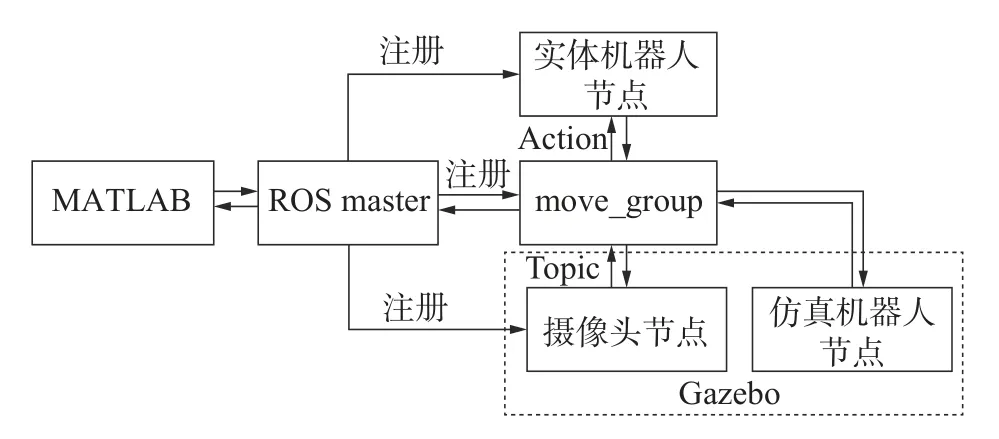
图8 仿真系统

4.2 视觉图像处理

为使仿真实验更贴合实际情况，在仿真环境中添加视觉传感器，在各个关节及机械臂末端设置圆形标记，通过视觉检测算法对标记物进行识别，并获取其中心坐标。获取图像信息后，首先进行图像预处理，将其灰度化减少运算量；再进行二值化操作，保留其形态信息的增强对比度，便于后续对标记物的识别检测[16]。由于成像变形，圆形标记物会变成椭圆，需要用椭圆检测算法进行识别。基于霍夫变换的椭圆检测算法需要确定描述椭圆的5 个参数，不可避免地出现了计算量大、耗时长等问题[17-18]。本文采用基于弧线段的椭圆检测算法。椭圆由若干弧线段组成，通过直线提取（line segment detector，LSD）算法对其进行检测[19]。把弧线段进行分组，通过对连续性和凸性的判定，即可得到2 个弧线段是否为同一组。分组完毕后，对跨度角进行判断，如跨度角近似等于360°，就将这组设置为初始椭圆集合。接着对描述椭圆的5 个参数分为椭圆中心坐标、长轴和短轴长度、旋转角度3 个子空间进行聚类，减小运算量，聚类完成后即可得到候选椭圆。为了保证检测结果的可靠性，从覆盖角度和边缘点数量2 个角度进行评分。覆盖角度越大、边缘点越多，说明得到的椭圆拟合效果越好，可选择出最优椭圆。图像处理流程如图9 所示。

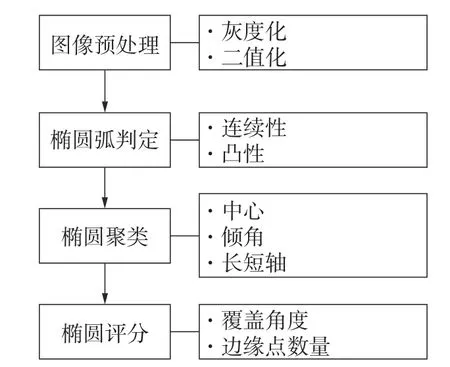
图9 图像处理流程

机械臂运动过程中，用视觉传感器1 和视觉传感器2 捕捉图像信息，提供关键点坐标，控制机械臂末端靠近目标点。随着二者之间的距离逐渐变小，会出现标记物部分重叠的情况，如图10 所示，此时无法识别椭圆。

图10 末端和目标物重合时椭圆检测

为了在标记物出现重合的情况下还能够准确识别，在目标物附近安装视觉传感器3，并设置阈值dm。当末端和目标物的距离大于该阈值时，用视觉传感器1 和视觉传感器2 获取图像信息，反之调用视觉传感器3。由于视觉传感器3 设置在目标物附近，不会出现成像变形，调用霍夫变换对圆的检测算法即可[20]，控制末端逐渐靠近目标物并完全重合，结果如图11 所示。

图11 末端靠近目标物并完全重合

4.3 仿真结果分析

在搭建好虚拟仿真系统并且完成图像处理后，开始进行仿真实验。仿真结果如图12 所示。从机械臂的末端位置变化曲线以及速度变化曲线可以看出，机械臂在初始阶段以较大的速度运行，在逐步靠近目标物时速度逐渐降低，并且曲线较为圆滑。最终末端与目标物之间的距离误差为4.21×10-6m，整个过程运动平稳，误差较小，说明本文建立的机械臂位置的模糊控制系统效果良好。

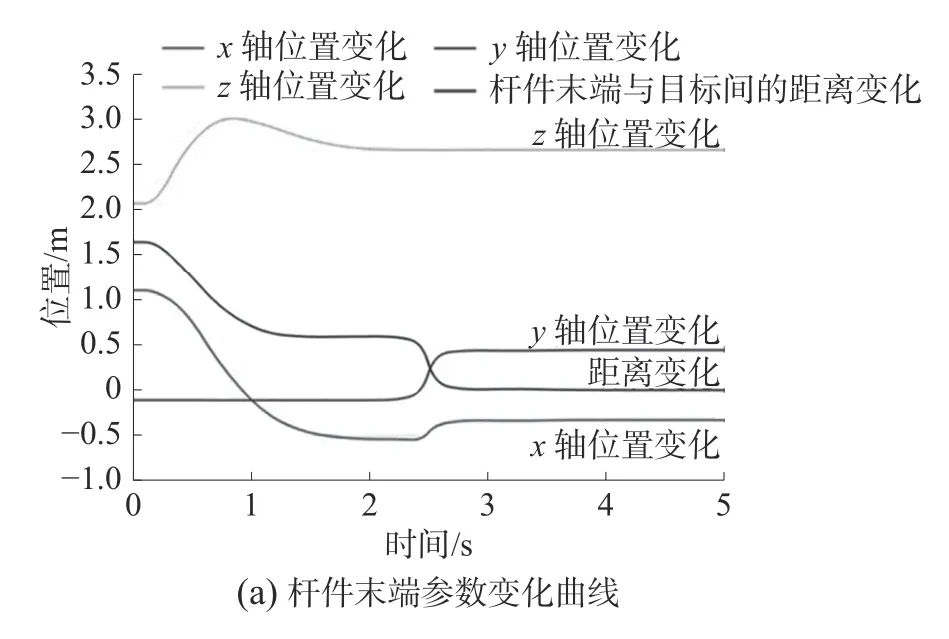
图12 仿真结果

5 柔性机械臂探究

通过三自由度机械臂的仿真实验，验证了模糊控制方法的可靠性。由于该方法不需要建立复杂的运动学模型，将其初步用于柔性机械臂的控制。在ROS 和MATLAB 的联合仿真中，目前只能建立刚性模型，因此用2 根刚性机械臂来近似模拟柔性机械臂。如图13 所示，在杆1 转动的过程中，调用函数得到杆1 某端的速度v，将kv作为关节2 的速度（k为任选常数），杆1 和杆2 之间就会形成夹角θ。随着杆1 的转动，关节1 和末端的距离不断变化，实现柔性机械臂的模拟。

图13 柔性机械臂模拟

仿真实验中，用来模拟柔性机械臂的刚性杆具有2 个自由度，并且都位于xoy平面上。将目标物设置在xoy平面，只需调用正视该平面的视觉传感器1 和目标物附近的视觉传感器3，运动方向的判断参照文中三自由度机械臂2 个共面转动关节的运动方向判断算法即可。其余流程与三自由度机械臂仿真实验一致，仿真结果如图14 所示。机械臂在初始阶段以较大速度运行，在靠近目标物的过程中速度逐渐降低。由于柔性机械臂长度的变化，在靠近目标物时产生了轻微波动，最终末端与目标物之间的距离误差为2.32×10-5m，验证了该方法同样适用于对柔性机械臂的控制。

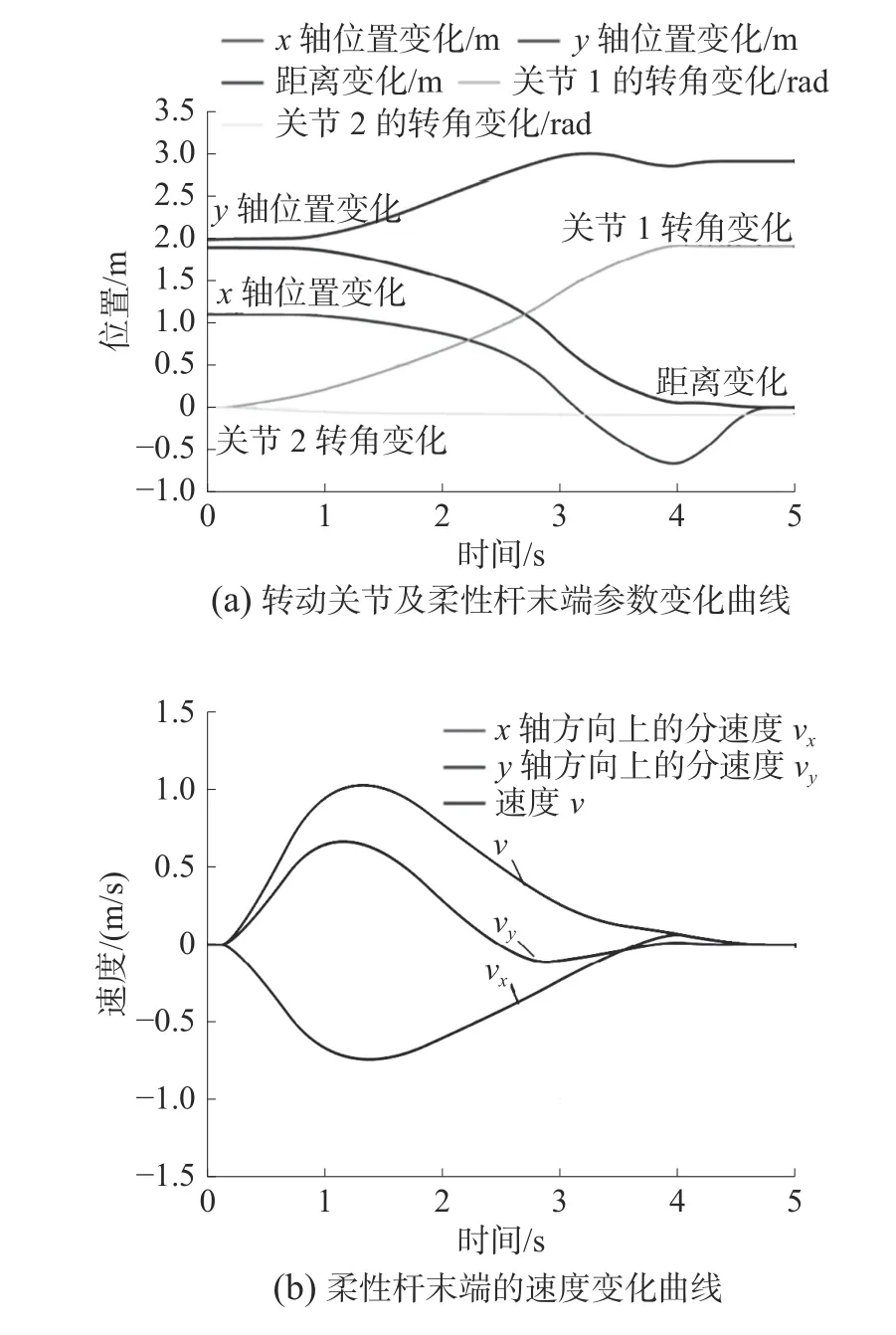
图14 柔性机械臂仿真结果

6 结论

本文提出了一种基于视觉反馈的机械臂位置的模糊控制方法，设计了运动方向判断算法和模糊控制器，并通过仿真实验验证了该控制系统的可靠性，得到结论如下：

1)该控制系统不受机械臂杆长的约束，适用范围广并且误差较小，具有快速性与较好的稳定性。

2)相比于传统的逆运动学解法，无需建立复杂的运动学模型，求解过程更简单，可用性强。

3)该方法已初步实现对柔性机械臂的控制，后续会对该方法进行深入研究，解决柔性机械臂控制过程中存在的建模复杂等问题，具有广泛的应用价值。