基于改进LightGBM的农机服务备件配置预测方法

温彦博,王 卓,白晓平

(1.中国科学院 沈阳自动化研究所,沈阳 110000;2.中国科学院 机器人与智能制造创新研究院,沈阳 110169;3.中国科学院大学,北京 100049)

0 引言

当前,农机产业进入了信息发展的新时期,发展面向农机服务网点的农机运维服务是提高农机产业信息化水平的重要举措。其中,实现各农机服务网点的农机服务备件配置精准预测是农机运维服务中最为重要的一环。然而,由于目前各农机服务网点对农机资源备件配置预测不准确,导致农机配件缺货或过度配置,进而使得面向农机服务网点的农机资源运维服务方面存在着大量的浪费和效率低下情况。例如,在农机损坏的情况下无法做到及时的维修处理,导致了在宝贵的农忙时期耽误了大量时间,使得农机作业效率降低,造成了较大的成本损失。所以,对农机服务备件配置精准预测,对于发展面向农机服务网点的农机运维服务和提高农机产业信息化水平进行具有重要意义。

近年来,随着我国农业信息化现代化的发展,一部分的学者也把目光放在了农机服务资源的备件预测问题上。孙硕将AHP层次分析法与传统的ABC分类相结合,并将经BP神经网络训练合格的网络用于备件需求量的预测[1]。周瑞基于遗传算法优化的灰色神经网络方法构建需求预测模型,预测了运维服务需求数量[2]。郭政杰基于知识挖掘为农机资源备件的预测提供了数据准备,并用贝叶斯网络对农机装备进行故障维修服务决策[3]。肖沙沙基于平衡计分卡和网络分析法构建应急服务站选址和服务车优化的数学模型,并运用改进的模拟退火算法进行问题求解[4]。通过对国内外农机服务资源备件预测方法的研究可以看出:国内对于农机领域的备件预测方法处在一个初步探索的阶段,仍有很大的发展空间,无论是数据集的构建,还是算法的选择,并没有因地制宜选择符合农机作业时限性、环境复杂性及地理位置分布性的算法[5-11]。

农机服务资源的备件预测问题归根结底是一个回归问题,而当今机器学习领域的热门研究方向集成学习[12]对于处理该类回归问题有较好的表现。它将一组弱学习器组合起来,后面的学习器对前面的学习器的错误进行更多的关注,达到比单一的强学习器更好的拟合效果,且效率更高。LightGBM作为集成学习的一员,在LGBT和XGBoost[13-14]的基础上进行改进,以更快的训练效率、更低内存使用得到更高的准确率[15-16]。为了更加高效且精确地对农机服务资源进行备件预测,将LightGBM模型引入农机服务资源备件预测领域。首先,分析并采集可能影响农机服务资源备件量的特征变量,并对这些特征数据与备件量的相关性分析处理,选取与预测结果相关性较大的特征建立数据集;然后,对基于LightGBM模型进行训练和测试,对农机服务资源进行备件预测。由于LightGBM超参数繁多且对参数的调整极大程度上影响了预测结果,故在LightGBM的基础上对于LightGBM的超参数使用PSO进行优化求解。这种改进相比于手动调参和网格搜索法调参能大大缩减参数寻优时间,并使得预测结果会更加精准。最后,通过测试对改进的LightGBM模型和原来的LightGBM模型的结果进行对比,采用均方根误差(RMSE)作为评价指标对结果进行总结。将LightGBM引入农机服务资源备件预测领域,颠覆了传统的农机备件方法,对于提高农机作业的效率、农机运维的信息化和智能化水平具有一定的意义。

1 LightGBM模型原理

LightGBM是一种基于分布式的GBDT梯度决策提升树的boosting高效算法,前一个决策树的残差用损失函数的负梯度来拟合下一个决策树。其相较于XGBoost,速度更快,精度更高,能使用更多的数据且速度不降低,同时能够在多机并行工作时做到线性加速。对于农机服务资源备件预测的多数据、多特征输入以及特征多为离散型高基数特征的情况,无需独热编码,避免了产生大量的新特征及维数灾难。在GBDT梯度决策提升树的基础上,LightGBM做了以下改进:基于Histogram的决策树算法,带深度限制的Leaf-wise的叶子生长策略,基于单边梯度采样(GOSS)和互斥特征捆绑(EFB)的特征数据处理。

1.1 基于Histogram的决策树算法

Histogram也就是直方图算法,其示意图如图1所示。图1中,左边直方图算法将每一个连续的特征数据重新按取值范围分组,映射成n个离散的整数,称为bin,这样就将存储降了下来;右边直方图通过特征对每一个bin数据进行统计并做梯度累加构建而成,并找到最佳切分点。

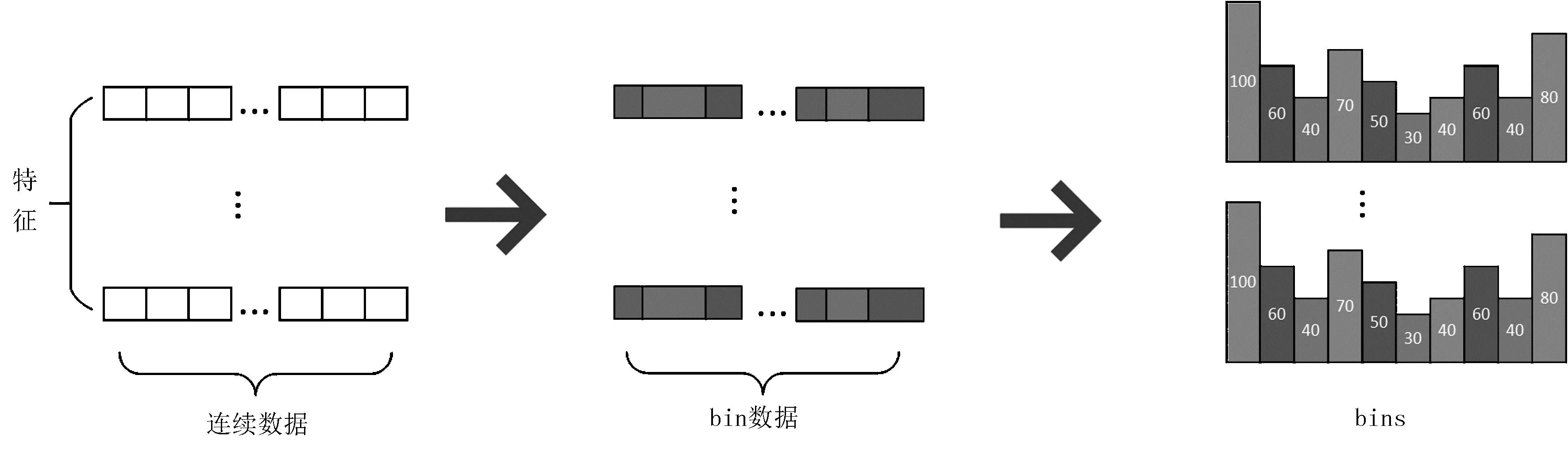
图1 Histogram的决策树算法示意图Fig.1 Schematic diagram of Histogram decision tree algorithm

LightGBM中直方图构建算法流程如下:将训练数据、树的深度和特征维度作为输入数据,因为要对树中的每一个节点构建直方图,所以遍历每棵树的深度,再遍历每一个节点,从中得到要使用的数据集,再遍历所有的特征并构建节点的直方图;然后,在数据集中遍历所有的数据,将直方图中每一个分桶作为bin,得到bins之后把梯度和个数相加,由此找到最佳的切分点;最后,根据最佳切分点更新节点集。

直方图做差如图2所示。LightGBM在构建叶子节点的直方图时,只计算一个叶子节点2的直方图,其兄弟节点3的直方图通过其父节点1的直方图和该节点的差作为直方图,这样就用更小的代价得到了子节点的直方图,速度为原来的两倍。

LightGBM为了寻求最佳切分点,首先遍历每一个bin并累加所有左节点的梯度SL和数量nL,如式(1)、式(2)所示。通过上述直方图做差的方法得到右节点的梯度和数量,再带入式(3)中求得增益,选择最大的增益节点作为最佳切分点。

SR=SP-SL

(1)

nR=nP-nL

(2)

(3)

虽然直方图算法在特征值离散化处理后找不到最精确的切分点,但实际上由于梯度决策树本身就是弱学习器,故采用直方图算法反而会起到正则化的效果,并且避免了模型的过拟合作用,即离散化的切分点对最终的精度反而更有利。

图2 直方图做差Fig.2 Histogramsubtraction

1.2 单边梯度采样算法(GOSS)

单边梯度采样算法(GOSS)和互斥特征捆绑(EFB)都是LightGBM降低特征数量以及样本数量的降维方法。在计算增益时,LightGBM采用的是一阶梯度和二阶梯度。本算法认为梯度越小时其误差越小,即表明此部分的样本已经训练完备;但是,如果直接丢弃这些样本会影响数据分布,而本模型中采用的是单边采样方式适配,即GOSS算法。其采样方式为:在进行最佳节点划分时,使用所有的大梯度样本以及一部分的小梯度样本。

GOSS的步骤如下:首先,计算增益并对其排序,选取其中a×100%的大梯度样本数据A,再从剩余的(1-a)×100%样本中选取b×100%小梯度样本数据B;由于小梯度样本整体分布减少,将小梯度样本数据放大(1-a)/b×100%倍,合并两者进行训练。

在原来的直方图算法中,若O为弱学习器在某一个分裂节点的数据集,则在j个特征、分割点d处的增益为

(4)

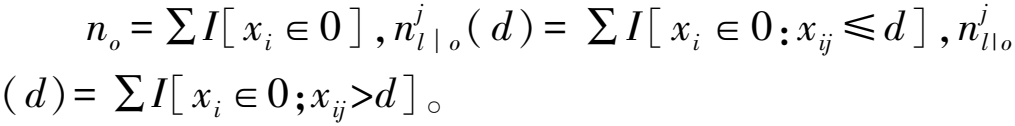
在GOSS算法中,若O为弱学习器在某一个分裂节点的数据集,则在j个特征、分割点d处的增益为

(5)

其中,A为上述的大梯度样本Al=xi∈A:xij≤d,Ar=xi∈A:xij>d;B为小梯度样本Bl=xi∈B:xij≤d,Br=xi∈B:xij>d。

1.3 互斥特征捆绑算法(EFB)

LightGBM根据高维数据的特征有很多稀疏且互斥的特性提出了互斥特征捆绑算法(EFB)。EFB为了特征的维度降低,将互斥的特征合并成一个特征“束”,称为bundle。通过贪心算法找到可以进行合并的特征,再通过互斥特征合并MEF(Merge Exclusive feature)算法将特征合并成一个bundle。

EFB算法通过贪心算法的图着色原理找到可以进行合并的特征。首先,对特征按从大到小的顺序排序;然后,新建一个bundle对图遍历。如果冲突很小,就划分到一个bundle中;如果冲突很大,就新建一个bundle。

MEF算法将特征合并成一个bundle,关键在于要确保原始特征可以从bundle中识别出来,如图3所示。由于直方图的算法存储的是离散的bin,而不是特征的连续值,所以可以通过向特征的原始值添加偏移量来实现。

图3 MEF算法原理示意图Fig.3 Schematic diagram of MEF algorithm

1.4 决策树生长方式

原来的决策树以Level-wise方法为生长策略,即对每一层的节点都进行一次分裂然后再剪枝。其优点在于容易进行多线程的并行化,而且不容易发生过拟合,如图4所示。但是,实际上有很多节点的分裂增益并没有那么高,对每个节点分裂搜索势必会导致决策树的生长效率降低。

LightGBM为了降低损失,对决策树的生长策略为Leaf-wise,即以每1个叶子节点的增益作为划分依据,如图5所示。在第一次分裂时,生成2、3两节点,3节点增益更大,故选取3作为下一个分裂点;比较剩余节点2、4、5等3个节点,4节点增益更大,故选取4作为下一个分裂点;比较剩余节点2、5、6、7节点,2节点增益更大,故选取2作为下一个分裂点。

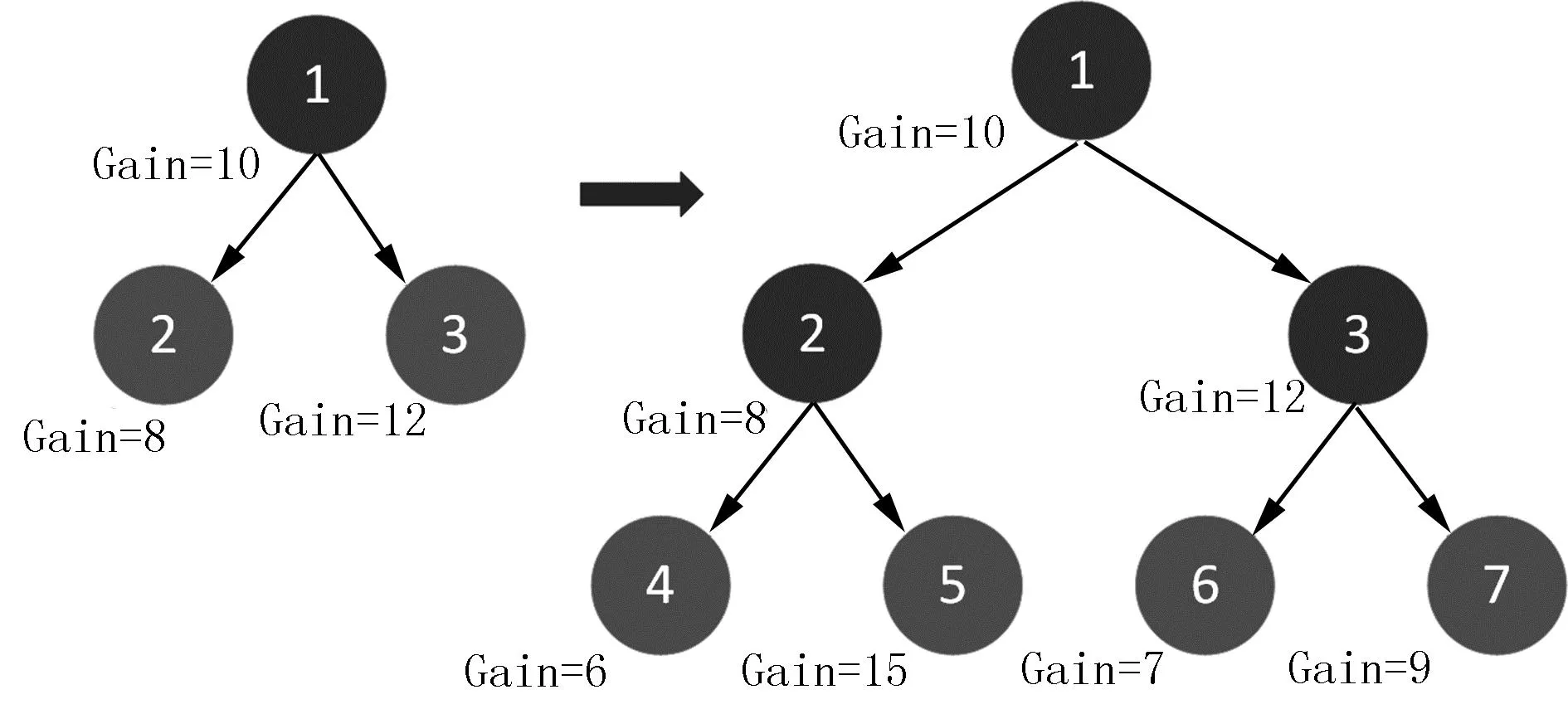
图4 Level-wise生长策略Fig.4 Level-wisegrowth strategy

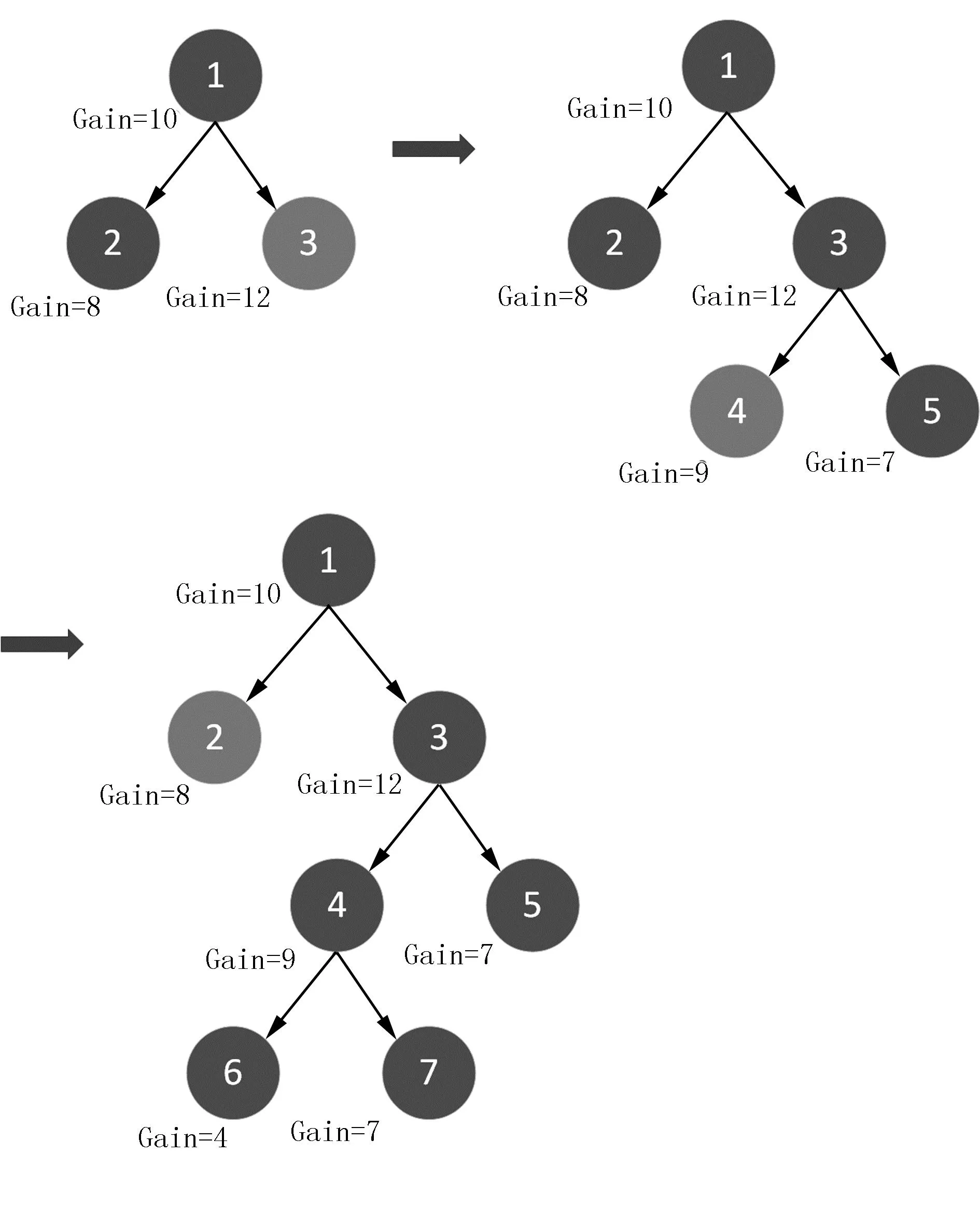
图5 Leaf-wise生长策略Fig.5 Leaf-wisegrowth strategy

1.5 基于PSO的LightGBM超参数优化

LightGBM算法针对leaf-wise树的参数优化及更快的训练速度,旨在获取更好的准确率,缓解过拟合有繁多的超参数。这些参数直接影响了算法的计算效率与准确度,故将PSO算法引进LightGBM中优化该算法中的超参数。

PSO算法作为一种群体智能优化算法,用粒子模拟鸟群中的鸟,粒子具有速度v和位置x两个属性。每一个粒子搜寻自己的个体最优解,然后把个体最优解与其他粒子共享,整个粒子群中的最优的个体最优解为当前全局最优解,所有粒子根据个体最优解和全局最优解来调整速度和位置。速度更新和位置更新的公式为

Vid=ωVid+C1random()(Pid-Xid)+

C1random()(Pgd-Xid)

(6)

Xid=Xid-Vid

(7)

其中,C1、C2为学习因子;Vid为粒子速度;Pid为第i个变量第d维的个体最优解;Pgd为第d维的群体最优解;ω为惯性因子,该值越大全局收敛能力越强,相应的局部收敛能力越弱。通常在算法初期选择较大的ω,以快速地寻找全局最优。该值越小,全局收敛能力越弱,相应的局部收敛能力越强。通常在算法后期选择较小的ω,以精细地寻找极值点。动态ω的更新公式为

ω(t)=(ωini-ωend)(Gk-g)/Gk+ωend

(8)

将LightGBM超参数作为PSO算法的输入,将其结果的MSE均方误差计算出来,作为PSO的适应度函数,寻求RMSE的最低值。

2 实验验证

2.1 影响因素分析及特征选择

农机作业环境复杂,种类繁多,影响农机服务资源储备的因素很多,且有很多类别型数据,无疑加大了精准预测的难度。为了更加全面地分析农机服务资源备件的影响特征,从农机作业环境信息、服务网点信息和备件信息3个方面综合全面地选择影响备件量的特征。

在农机作业环境信息方面,一般来说温度越高、湿度越高对农机的自然损耗越大,越容易造成农机零部件的需求量增加;反之,气候越干燥,对农机的自然损耗越小,越容易造成农机零部件需求量的减少。地理条件越恶劣的地方,越容易造成备件需求量的增加;地理条件越优越的地方,越不容易造成备件需求量的增加。

在服务网点信息方面,按照经验,每个农机服务网点所覆盖的农机作业面积与备件需求量成线性关系。例如,农机持有量越多,农机的作业强度越大,对备件的需求量也越大,应作为主要的参考特征。同时,农机类型以及农机的作业类型也与备件量有着千丝万缕的联系。

在零部件信息方面,本文选取了配件类型、配件名称、配件型号、配件价格、制造厂商、配件市场需求量、配件在服务网点的消耗量等多维信息作为特征输入。

2.2 特征处理及相关性分析

对于对照组的其他算法,需要对数值型数据进行归一化处理,如式(9)所示。其中,x为原始数据,x′为归一化处理后的数据。对于气候信息、地理环境等信息,将其分为[好 坏]等类别型数据,并进行独热编码处理。对于LightGBM模型来说,本质是上文提到的直方图算法,不需要对数据进行归一化和独热编码处理。直方图算法对于数值型特征以及类别性特征有着不一样的分bin策略。对于数值型特征而言,首先对特征进行去重,并按从大到小的顺序排序对每一个特征值统计个数;然后,比较最大的分bin个数和去重后的特征值个数,选取更小的那个作为直方图分bin的数目;最后,计算每一个bins中的平均样本个数,即用特征值个数与分bin的数目相除。如果有某一个bins中的个数大于平均样本个数,就取该值作为bins上限,并选取小于平均样本个数的第1个值作为bins下限;如果有某一个bins的个数小于平均样本个数,那么需要对其累加并分组。对类别型的特征用数值进行排序,首先对特征值统计出现的次数,并按从大到小的次序进行排序;然后,和数值型特征一样,比较最大的分bin个数和去重后的特征值个数,选取更小的那个作为直方图分bin的数目;最后,将特征值和bin结合起来进行最佳点的划分。

(9)

对于有空缺值的数据采用折中法,即对于数值类型特征取中位数,如式(10)所示。其中,m为所有不为空值数据的数量,对于分类类型特征取None。

(10)

遍历每一个类别型特征,对于有某一种类别占该特征总类别数大于70%的特征,认为该特征不具有有效性,删除该特征不进行训练。

查看训练集数据各特征之间的相关性,并对其分析可发现:对于数值型数据(见图6～8),农机作业面积、农机作业强度以及农机保有量有较强的相关性,即农机作业面积越大、农机作业强度越强、农机保有量越多,所需要的备件量越大,反之亦然,基本符合上文对备件量影响因素的分析。

图6 农机作业面积与备件量相关性示意图Fig.6 Schematic diagram of correlation between cultivated area and count

图7 农机作业强度与备件量相关性示意图Fig.7 Schematic diagram of correlation between cultivated force and count

图8 农机保有量与备件量相关性示意图Fig.8 Schematic diagram of correlation between machinery count and count

类别型数据(见图9～图12)分别为气候因素、地理环境、农机维修次数以及农机工作年限对备件量的影响,可以看出:气候潮湿、地理环境恶劣、农机维修次数越多,农机工作时间越长,对农机零部件消耗量越大,反之亦然,也符合上文对备件量影响因素的分析。

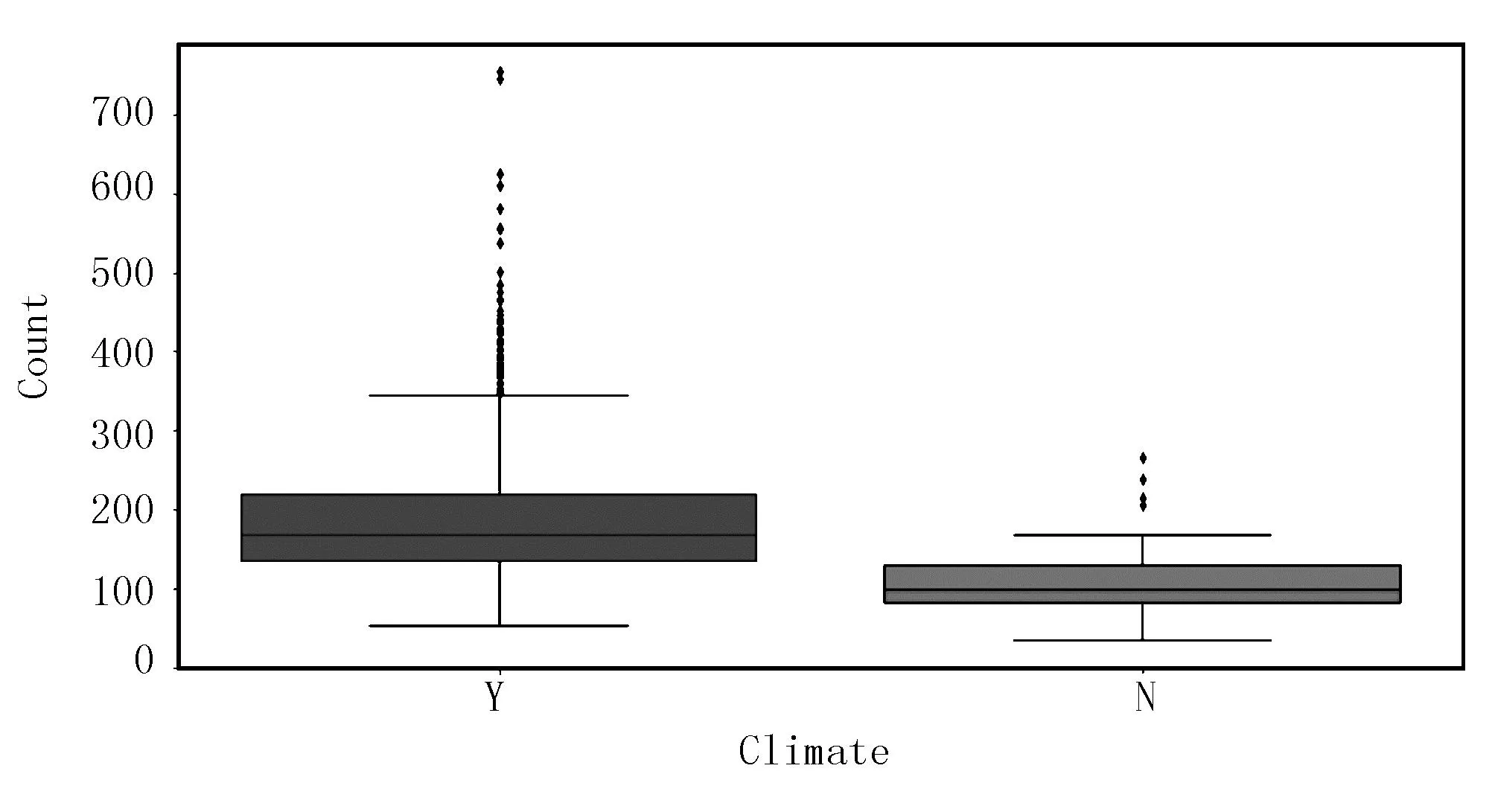
图9 气候因素与备件量相关性示意图Fig.9 Schematic diagram of correlation between climate and count

图10 地理环境因素与备件量相关性示意图Fig.10 Schematic diagram of correlation between environment and count

图11 农机保养情况与备件量相关性示意图Fig.11 Schematic diagram of correlation between service cod and count

图12 农机工作年限与备件量相关性示意图Fig.12 Schematic diagram of correlation between work life and count

2.3 模型训练

实验选用1460条备件数据,将农机作业环境、服务点信息以及备件信息三大维度内的多个上述特征作为输入,将训练集与测试集以3:1的比例划分,用LightGBM算法完成对备件量的拟合预测,以均方根误差RMSE作为评价标准。选用线性回归、随机森林、XGBoost算法作为对比验证,则

(10)

模型验证结果如表1所示。由表1可以看出:集成学习的算法随机森林、XGBoost、LightGBM的RMSE值28.63、28.43、27.67远小于线性回归的RMSE值41.94,在本问题的求解上有较好的表现;而对比LightGBM与随机森林、XGBoost,LightGBM的RMSE值27.67比随机森林和XGBoost的RMSE值28.63和28.43有一定的进步。

表1 模型验证结果

LightGBM算法的超参数繁多,合理地调整超参数能使模型的预测结果更加精确。因此,将LightGBM的超参数分为两大类,即核心参数和默认参数。核心参数的调整对于结果的准确性有较大的影响;默认参数使用模型默认的值就可以有很好的效果,故使用默认值,如min_split_gain,min_child_sample,min_child_weight。在此,核心参数被分成根据经验确定的超参数以及通过算法调优确定的超参数。根据经验确定的超参数n_estimators迭代次数设置成1000,boosting_type经验证设置成gbdt在本模型上效果更好。通过算法调优确定的超参数及取值范围表2所示。

表2 超参数取值范围

在进行参数调优时,人们常常采用网格搜索法grid search进行寻优。虽然用网格搜索法能找到最高的精确率,但对于像本模型如此大的算例和多维的特征时往往很耗费时间,而使用PSO的群智能启发算法就可以避免使其遍历所有的点就可以找到最佳参数。工作时,使用PSO算法对LightGBM参数进行调优。先初始化表2中的LightGBM超参数初始值,将RMSE评价标准作为PSO的适应度函数,不断更新每个粒子的个体最优值和群体最优值,直到找到使RMSE达到最小的参数,流程如图13所示。

2.4 实验结果分析

将上述超参数作为输入,维数为8,粒子群的种群规模设置为40,最大迭代次数为200,ω惯惯性权重设为0.8,个体记忆c1为0.5,群体记忆c2为0.5,迭代直到找到使RMSE达到最小的参数,结果如表3所示。

通过PSO的超参数寻优求解,得出PSO-LightGBM的RMSE,并用贝叶斯优化算法Bayesian Optimization参数调优作为对照,结果如表4所示。

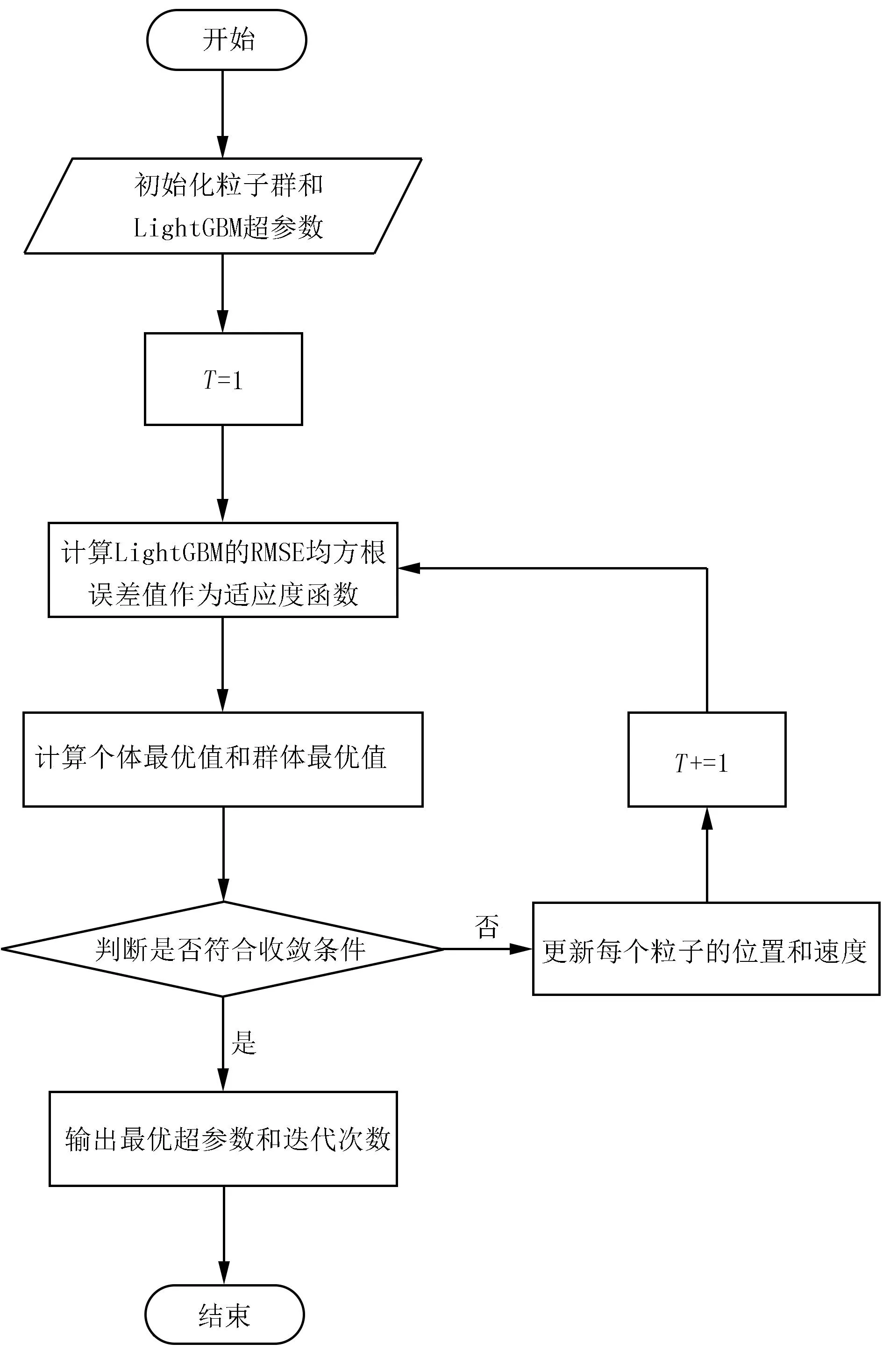
图13 PSO-LightGBM流程图Fig.13 PSO-LightGBMflow chart

表3 PSO-LightGBM超参数寻优结果Table 3 PSO-LightGBM hyper-parameter results

表4 模型验证对照表

续表4

表4中,对比LightGBM和BO-LightGBM、PSO-LightGBM,可以看出:BO-LightGBM、PSO-LightGBM的RMSE值25.84和24.74小于LightGBM的27.67。通过超参数调优后,LightGBM算法的RMSE值有明显的降低,大大提高了LightGBM算法的精度。

对比可知:BO-LightGBM的RMSE值24.74小于PSO-LightGBM的RMSE值25.84。因此,使用PSO调优的结果比贝叶斯优化的结果更好。

3 结论

根据农机在服务网点备件配置预测不准确导致农机服务资源备件浪费的问题,提出了一种基于改进LightGBM的农机服务资源的备件预测方法。确定了农机作业环境信息、服务点信息以及备件信息三大维度内的多个特征,验证了影响农机服务资源需求量的主要影响因素。基于LightGBM建立了农机服务资源备件预测模型,并使用PSO算法对模型的超参数进行调优。实验验证表明:与随机森林、XGBoost等算法相比,LightGBM模型有更好的效果,RMSE值为27.67。通过PSO的超参数调优,LightGBM备件预测的精确性更进一步,RMSE值为24.74,能够较为准确地预测农机服务资源在服务网点的备件需求。今后,在获得更多精准数据的基础上,将会不断优化该算法模型,主要方向是提升算法的优化速度。