双(G/G′，1/G)展开法求解（3+1）维mKdvZK 方程和（3+1）维YTSF 方程的新孤子解

杨 超，孙峪怀，韩梦娜

（四川师范大学 数学科学学院，四川 成都 610066）

非线性演化方程（NLEEs）被广泛应用于固体物理、相对论物理、光纤、化学物理、化学运动学、流体力学以及平面波传播、河流流动等方面，促进了物理学、化学和材料科学的发展，非线性演化方程的研究越来越受到关注。因此，学者们提出了许多求解非线性演化方程的方法，如雅各比椭圆函数展开法［1］、辅助方程法［2］、改进F展开法［3］、Hirota 双线性［4］、广义Kudryashov 法［5］、exp 函数法［6］、tanh 函数法［7］和改进的(G/G′)展开法［8］、一次积分法［9］、改进Khater 法［10］和扩展直接代数法［11］等。许多学者都倾向于使用双(G/G′，1/G)扩展法，这种方法比之前的技术更加高效可靠。例如Chowdhury 等［12］研究纳米离子电流方程和孤子方程，得到三角函数解和双曲函数解，Iqbal 等［13］给出修正Zakharov-Kuznetsov 方程和Gerdjikov-Ivanov 方程的t型、Kink 型、钟型、奇异解以及完整行波解的周期奇异解。Khatun 等［14］给出修正Camassa-Holm（MCH）方程的双曲函数、三角函数和有理函数，以及广义（3+1）维时空（gCH-KP）方程表示的孤波解。此外定义了以下（3+1）修正Korteweg-de vries-Zakharov-Kuznestsov 方程［15］

其中，U(x，y，t)是该方程的因变量，t是时间变量，x，y，z是空间变量，系数b非零。Tasbozan 等［16］用直接代数方法求解方程（1），Yaslan 等［17］确定解以及几种不同类型的mKdVZKE 解，Arslan 等［18］统一了解析方法求解不同分数参数的孤子解。

对于（3+1）维Yu-Toda-Sassa-Fukuymama（YTSFE）方程［19］

其中，U(x，y，t)是该方程的因变量，t是时间变量，x，y，z是空间变量。

Cevikel 等［19］使用扩展tanh-coth 法、sine-cosine 方法和(G/G′)展开法求解方程（2）的周期解和周期奇异解。本文用双(G/G′，1/G)展开法讨论λ不同取值范围时（3+1）维mKdvZK 方程和（3+1）维YTSF 方程从而获得其新形式的精确解。

1 双(G/G′，1/G)展开法求解过程

考虑以下非线性演化方程（NLEEs）

步骤1行波变换

将式（4）代入式（3），得到常微分方程

步骤2假设方程（5）的精确解具有如下形式：

且ϕ，ψ满足等式

其中μ，λ是待求常数。

以下分类讨论基于上述G(ξ)常微分方程的通解。

对于λ＜0，

对于λ=0，

其中A1、A2为任意常数。

步骤3将式（6）代入方程（5），合并与ϕ和ψ相关的同类项，使其系数均为零，得到一系列关于未知参数的方程组，然后根据关于G(ξ)的常微分方程的通解，将未知参数代入式（6）中的方程，从而得到非线性演化方程的精确解。

2 求解（3+1）维mKdvZK 方程

对方程（1）进行行波变换

由此得到

对式（16）进行一次积分，可以得到

通过平衡式（17）中的最高阶线性项和最高阶非线性项，得到n=1，可以假设方程（1）有如下形式的解：

情况1对于λ＜0，

将方程（1）的结果代入式（18），根据式（9）和式（10）得出以下精确解：

其中ξ=my+nz，b=b。

其中ξ=my+nz+kt，b=b。

其中ξ=my+nz，b=b。

情况2对于λ＞0，

将方程（1）的结果代入式（18），根据式（11）和式（12）得出以下精确解：

其中ξ=my+nz，b=b。

其中ξ=my+nz+kt，b=b。

情况3对于λ=0，

将方程（1）的结果代入式（18），根据式（13）和式（14）得出以下精确解：

其中ξ=my+nz，b=b。

当参数A1，A2，μ，l，m，n，λ，a0，a1，b1取特殊值时，u4，u7的三维图和二维图如图1 和图2 所示。

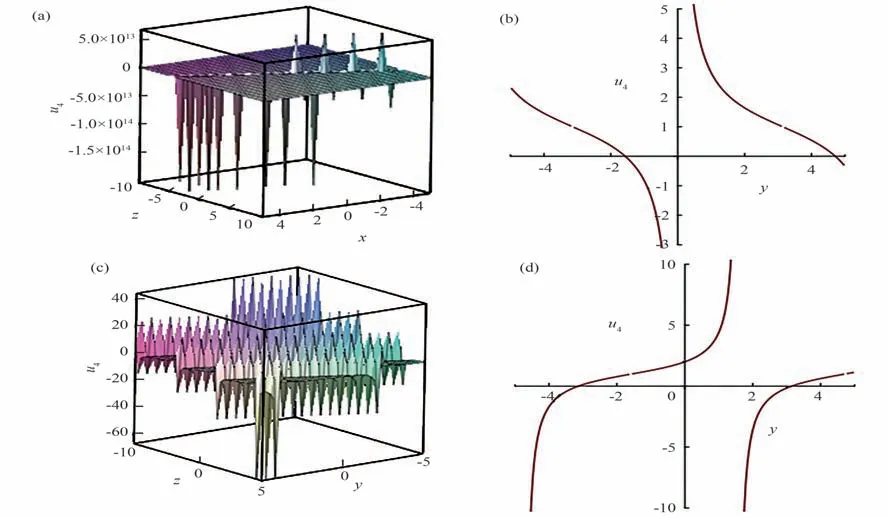
图1 u4 三维图和二维图Fig.1 3D and 2D drawings of u4

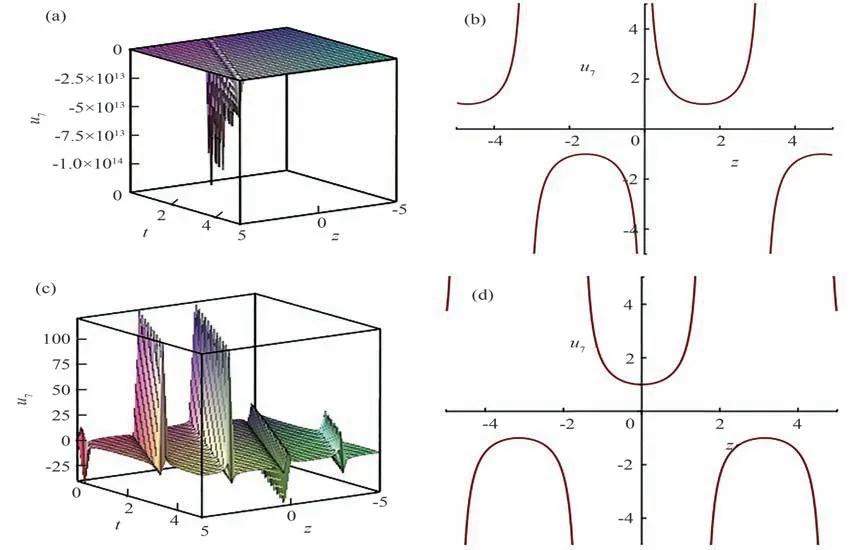
图2 u7 三维图和二维图Fig.2 3D and 2D drawings of u7

3 求解（3+1）维YTSF 方程

对方程（2）进行行波变换

由此得出

平衡式（17）中的最高阶线性项和最高阶非线性项，得出m=1，则认为方程（2）有如下形式的解：

情况1对于λ＜0，

将方程（2）的结果代入式（29），根据式（9）和式（10）得出以下行波解：

其中ξ=x+y+z-ct。

其中ξ=x+y+z-ct。

情况2对于λ＞0，

将方程（2）的结果代入式（29），根据式（11）和式（12）得出以下行波解：

其中ξ=x+y+z-ct。

情况3对于λ=0，

将方程（2）的结果代入式（29），根据式（13）和式（14）得出以下行波解：

当参数A1，A2，μ，y，z，c，λ，a0，a1，b1取特殊值时，u1，u7的三维图和二维图如图3 和图4 所示。

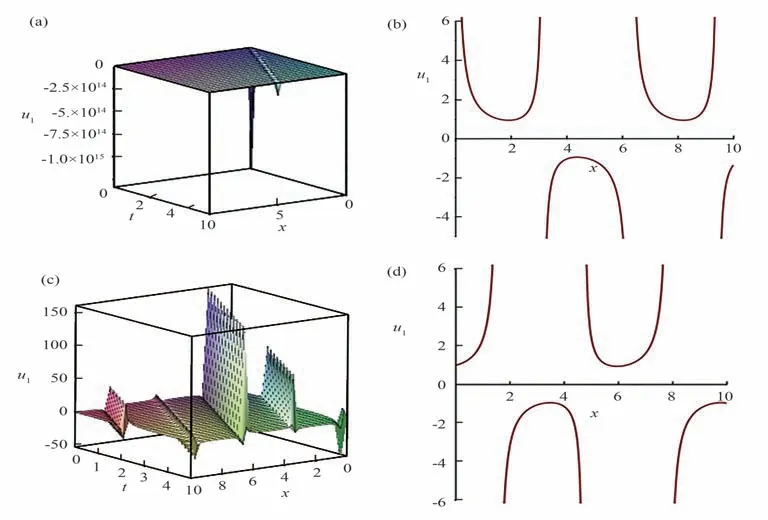
图3 u1 三维图和二维图Fig.3 3D and 2D drawings of u1

图4 u7 三维图和二维图Fig.4 3D and 2D drawings of u7

4 结论

本文通过行波变换和代入变换将（3+1）维mKdvZK 和（3+1）维YTSFE 转化为常微分方程，然后利用双(G/G′，1/G)展开法得到两个方程的新精确解。对于mKdvZK，其中u1、u4与文献［15］中式（4.29）相似，u5与文献［18］中式（4.32）相同，同时u1、u2、u3、u6、u7、u8与已有的文献不同。对于YTSFE，其中u1、u2、u3与文献［19］中式（5.28）、（5.29）相同，u6与文献［19］中式（5.30）相似，同时u4、u5、u7与现有的文献不同。该方法适用于求解非线性演化方程，能够提供了大量新的精确解，在实际应用中具有重要意义。