参数依赖延迟的Gray-Scott 模型稳定性和分支分析
肖 越,马淑芳
(东北林业大学 理学院,黑龙江 哈尔滨 150040)
Gray-Scott 模型[1-2]是一种重要的反应扩散系统,起源于模拟自催化化学反应,其化学反应过程为
其中U,V为两种化学物质,V作为催化剂对自身生产起催化作用,P为一种惰性产物,不参与反应过程。该反应过程的无量纲反应扩散方程形式为
其中u(x,t),v(x,t)分别表示在x点处t≥0 时抑制剂与催化剂的浓度,a表示入流率,a+b表示催化剂V的移出率,Du和Dv分别表示化学物质U,V的扩散系数。
迄今,已有许多文章从不同的角度对系统(1)进行了研究[3-12]。2009 年,Kyrychko 等[11]对系统(1)施加了延迟反馈控制项
其中f(u,v)=-uv2+a(1-u),g(u,v)=uv2-(a+b)v,K为反馈强度,A为2×2 的控制矩阵。研究控制矩阵A取(ϕ是相位)等情况时,延迟反馈控制对系统(2)的时空斑图的影响。在每种情况下,在控制强度和时滞的参数空间中找到了稳定边界。在时空混沌的情况下,施加的控制既可以稳定均匀稳态,也可以导致平凡稳态和传播行波之间的双稳态。
此外,为了获得关于系统(1)的动力学的信息,研究者也对常微分系统进行了讨论。
系统(3)是系统(1)中Du=Dv=0 的情形。文献[12]研究了系统(3)对应的三次多项式系统在庞加莱盘中的相位图。相位图和相应的分岔图显示了这类系统的丰富性和复杂的动力学。
基于上述讨论,本文将研究如下形式的一类具有延迟反馈项Gray-Scott 模型:
其中,p>0,τ>0 表示延迟;K是常数,Ke-pτ表示延迟反馈强度。受过去历史记忆消退效应的启发,延迟反馈强度随着延迟τ的增加而衰减,当延迟τ趋于无穷时,反馈就消失。对于依赖于延迟的反馈控制研究也已取得了很多成果[13-16]。通过研究成果可以看出,参数对延迟τ的依赖性使得系统的动力学性质变的更加复杂。本文选择延迟τ和衰减率p作为分岔参数,将分析系统(4)产生Hopf 分岔和稳定转换的条件。
1 正平衡点的稳定性和Hopf 分支的存在性
经过计算,系统(4)存在三个平衡点,分别为
在平衡点E1处将系统(4)线性化,得
系统(4)的特征方程为
令λ=iω,分离实虚部,得到
令θ=ωτ,由于τ∈[0,+∞),从而θ∈[0,+∞)。由式(7)可推得
化简得
解得
显 然,若K<0,>max(a,b),有sinθ>0,ω+>0;若K>0,>max(a,b),有sinθ<0,ω->0。本文仅考虑K<0,>max(a,b)情况(K>0,>max(a,b)讨论方法类似)。
根据式(7),有
进一步,有
令θ=θ0+2nπ,n=0,1,2…,由于sinθ>0,那么θ0∈(0,π)。
当τ=0 时,方程(5)变为
讨论τ>0 的情况。由于θ满足式(12),且减小p的值或增大τ的值会导致θ的个数持续增加,这种变化同时也会引起Hopf 分支。由式(12)中p=p+的几何图,可以直观看到Hopf 分支的出现频率,如图1 所示,其中n=0,1,2,3 的情况分别由蓝色、橙色、黄色、紫色线条表示。根据图1 可得以下结论:
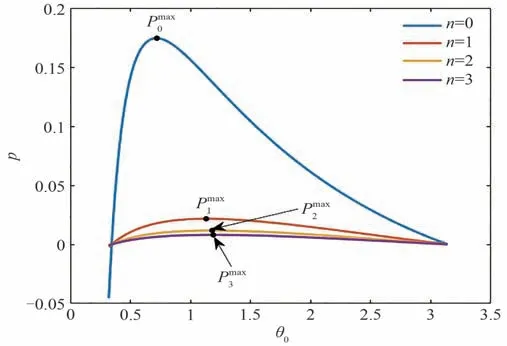
图1 式(12)确定的参数p 关于θ0 的值Fig.1 The values of parameter p versus θ0 determined by equation(12)
(1)若p>,特征方程(5)不存在纯虚根,此时不产生Hopf 分支,系统(4)对所有的τ>0 都是稳定的;
(3)若p=,特征方程(5)存在(2n+1)个纯虚根,这表明随着时延迟的改变系统(4)会发生(2n+1)次Hopf 分支。
对每个n,都能通过计算最大值。由式(12),有
而由式(9),有
结合式(13)与式(14),有
其中
讨论系统(4)的稳定性转换和Hopf 分支。对于给定的τ,假设方程(5)存在一组共轭根λ=α(τ)±iω(τ)。为了简单起见,定义τc=τn,ωc=ωn(n=0,1,2…),此时有α(τc)=0 以及ω(τc)=ωc,对方程(5)关于τ求导,有
将式(11)代入式(16),化简得
同时,由于
结合之前的研究,可知系统(4)在τ=0 时是稳定的。当τ继续增大时,情况保持不变,直到对应一对实部为零的特征根的第一个临界值τ0的出现,此时系统开始由稳定变为不稳定状态,并在τ0处产生Hopf 分支;当τ继续增大到第二个临界值τ1时,系统由不稳定再次变为稳定状态。因此在(τ,p)平面内形成了一个稳定域,如图2 所示,阴影部分即为稳定域,并且在这个区域的边界上会产生Hopf 分支。
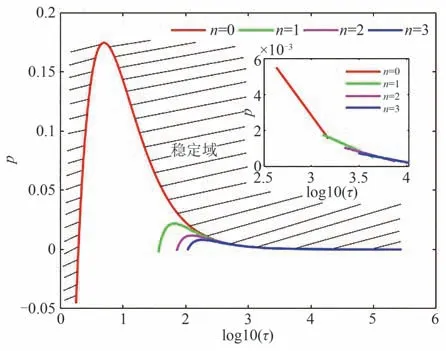
图2 当a=0.1,b=0.02,K=-0.5 时,系统(4)在(τ,p)平面上的Hopf 分支曲线Fig.2 Hopf bifurcation curves of system(4)in the (τ,p) plane for a=0.1,b=0.02,K=-0.5
2 数值模拟
令a=0.1,b=0.02,K=-0.5,p=0.1,此时平衡点E1=(u1,v1)=(0.174,0.688)。计算可知满足假设条件sinθ>0,>max(a,b)。基于前文研究,当τ=1 时,E1是稳定的,如图3 所示;当τ=2.514时,产生周期解,如图4 所示。此外,随着τ的继续增大,解将趋于常值平衡点E0。另外,根据文献[11]可知在远离图灵和Hopf 区域的参数范围内,系统总是以E0或E1结束。在图5 给出了τ=3 时,系统在E0处结束。
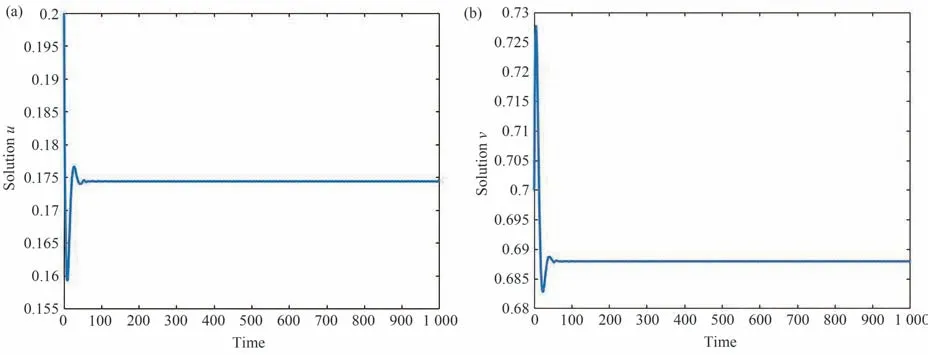
图3 当τ=1 时,系统(4)的时间序列曲线Fig.3 Time series curves of system(4)when τ=1
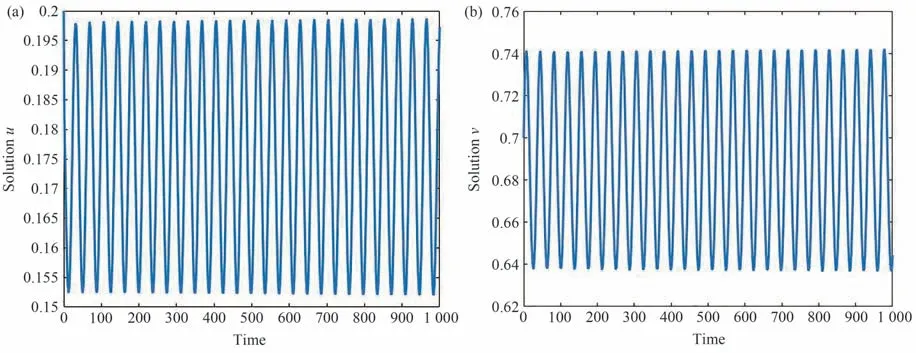
图4 当τ=2.514 时,系统(4)的时间序列曲线Fig.4 Time series curves of system(4)when τ=2.514
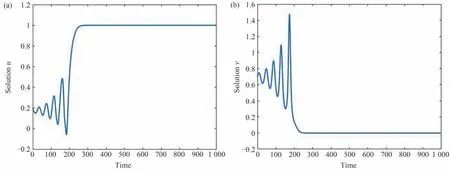
图5 当τ=3 时,系统(4)的时间序列曲线Fig.5 Time series curves of system(4)when τ=3
3 小结
本文研究了一类具有延迟反馈控制的Gray-Scott 模型,其中反馈控制强度为Ke-pτ。这种参数依赖于延迟的反馈控制,使得系统的稳定性以及分支分析变得更加复杂。研究给出了确定平衡点稳定条件的几何方法和解析方法,并讨论了该模型的Hopf 分支。主要结果如下:
(1)除时滞τ外,系统(4)的Hopf 分支强烈依赖于参数p,虚特征根的横截条件由参数p(θ)变化决定;
(2)在(τ,p)平面上作出了系统(4)的Hopf 分支曲线,并且标记出了稳定域(图2);
(3)本文通过数值模拟的方法验证了当τ持续增大时,系统(4)会由稳定状态转为不稳定状态。

