有向图是极大弧连通的充分条件

徐 兰

(昌吉学院数学系,新疆昌吉 831100)

0 引 言

本文只考虑D=(V,A)是一个没有自环和平行弧的有向图.设点 v∈V,分别用 d-D(v)、d+D(v)(简写为,d-(v)、d+(v)),记为 v的出度、入度,δ-(D)、δ+(D)为 D的最小入度、最小出度,且D的最小度记为,δ(D)=min{δ-(D),δ+(D)}.

强连通有向图D的弧割,是指去掉这个弧割后D不再强连通.弧连通度λ(D)是一个最小弧割的基数.D是极大弧连通的,如果λ=δ.设X,Y⊆V,且(X,Y)表示尾巴在X中,头在 Y中的弧集.和 K→n,m分别是完全有向图与完全二部有向图.文中未提到的定义与术语可参见文献[1]中相关表述.

无孤立点的有向图D的逆度定义为:

图的逆度最早在文献[2]中被提出,且被许多作者研究[3,5].本文将给出关于R(D)、δ(D)和 n阶有向图是极大弧连通的充分条件.

1 主要结果

引理1[6]设D为强连通的有向图,其弧连通度为λ.如果存在不交集合,X,Y⊂V(D),有X∪Y =V(D),|(X,Y)|=λ＜δ,那么,|X|,|Y|≥δ+1.

引理2[4](1)设 a1,a2,…,ap,A是正实数,且

(2)如果 a1,a2,…,ap,A是正整数,且 a,b是整数,有A=ap+b,0≤b＜p,则,

等式成立的充要条件是p-b个ai等于a,其余的ai等于a+1.

(3)设f(x)是在[L,R]上的连续凸函数,且l, r∈[L,R],l+r=L+R,则,

定理1 设D为强连通的有向图,其弧连通度为λ,最小度为δ.如果,

则,λ=δ.

证明 假设,λ≤δ-1.由引理1,存在不交集合 X,Y⊂V(D),使得,X∪Y=V(D)和|(X,Y) |=λ＜δ.有,δ+1≤|X|,|Y|≤n-δ-1.则,

根据引理2之(1)有,

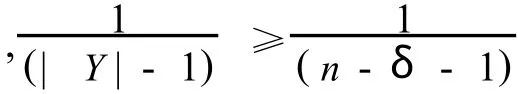
又因为,λ≤δ-1,则,

矛盾.

推论1[4]设 G是n阶连通图,其最小度为δ,边连通度为λ,如果,

则,λ=δ.

下面用实例说明定理中的界是紧的.

例1 设 n和δ是正整数,且 n≥2δ+2≥8,进一步,设 K→δ+1的点集为,V(K→δ+1)={x1,x2,…, xδ+1},K→n-δ-1的点集为,V(K→n-δ-1) = {y1,y2,…, yn-δ-1}.定义图 D是K→δ+1与K→n-δ-1的并集,再加上2(δ-1)条弧,x1y1,x2y2,…,xδ-1yδ-1;y1x1,y2x2,…,yδ-1xδ-1.则,δ(D)=δ,且,

容易得到,

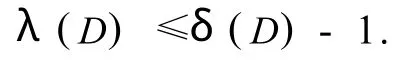
设D是二部有向图,其二部分化为,V(D)=V′∪V″.设X是V(D)的子集,令X′=X∩V′,X″= X∩V″.

引理3[6]设D是强连通的二部图,其弧连通度为λ,最小度为δ.如果λ＜δ,则存在不交集合X,Y⊂V(G),且 X∪Y=V(G),|(X,Y)|=λ,使得,|X′|,|X″|,|Y′|,|Y″|≥δ,即,|X|, |Y|≥2δ(G).

定理2 D是n阶强连通的二部图,其弧连通度为λ,最小度为δ.如果,

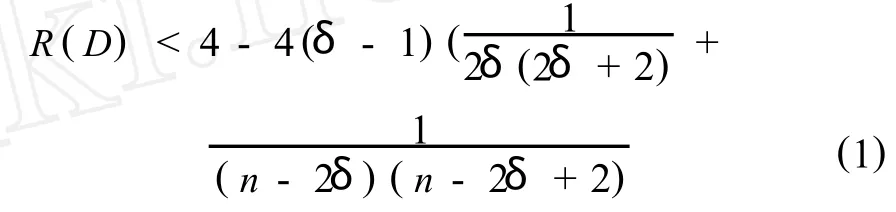
则,λ=δ.

证明 假设,λ ≤δ-1,则存在,X,Y⊂V(D),X∪Y=V(D),|(X,Y)|=λ,使得,|X|, |Y|≥2δ(D).因此,δ≤

因为D[X]是二部有向子图,则,

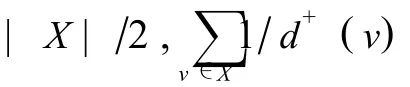
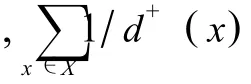
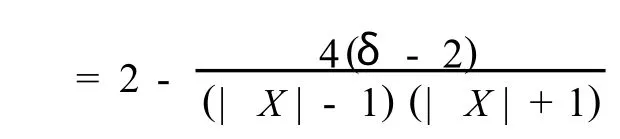
下面分3种情形进行讨论.

情形1 n是偶数,且|X|是偶数.则,|Y|= n-|X|也是偶数.由上面的不等式有,

所以,

矛盾.

情形2 n是偶数,且|X|是奇数.则,|Y|= n-|X|是奇数,有,|X|,|Y|≥2δ+1.和情形1类似,有,

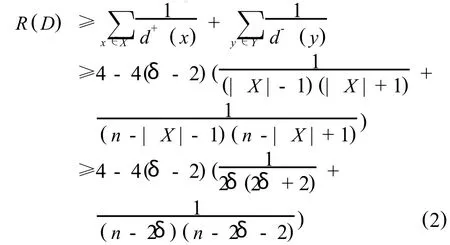
通过计算可知,(2)大于(1),矛盾.

情形3 n是奇数.不失一般性,设|X|是奇数,且|Y|是偶数.则,|X|≥2δ+1.类似情形1, 2,有,

通过计算可知,(3)大于(1),矛盾.

下例说明定理中的界是紧的.

例2 设 n,δ为正整数,且 n是偶数,n≥4δ,设D是由K→δ,δ=(A,B)与K→n/2-δ,n/2-δ=(C,D)的不交并得来的.这里,(A,B)与(C,D)是二部划分.分别在A与C中选择δ-1个独立点a1,a2,…,aδ-1和c1,c2,…,cδ-1,并添加2(δ-1)条弧 a1c1,a2c2,…, aδ-1cδ-1;c1a1,c2a2,…,cδ-1aδ-1,则 D是二部图,且λ=δ-1及逆度为,

定理中的界是紧的得证.

[1]BondyJ A,Murty U S R.Graph Theory and Its Application[M]. London:Academic Press,1976.

[2]Fajtlowicz S.On Conjectures of Graffiti(II)[J].Congr Numer, 1987,60(1):189-197.

[3]Dankelmann P,Swart H C,van den Berg P.Diameter and Inverse Degree[J].Discrete Math,2008,308(5-6):670-673.

[4]Dankelmann P,Hellwig A,Volkmann L.Inverse Degree and Edge-connectivity[J].Discrete Math,2009,309(9):2943-2947.

[5]Erdǒs P,Pach J,Spencer J.On the Mean Distance Between Points of a Graph[J].Congr Number,1988,64(1):121-124.

[6]Hellwig A,Volkmann L.Maximally Connected Graphs[D].Hellwig,Angelika:RWTH Aachen University,2005.

[7]Geller D,Harary F.Connectivity in Digraphs[J].Lecture Notes in Mathematics,1971,186(1):105-115.