解多目标规划最小弱有效解的动约束组合同伦方法
何 非,商玉凤
(空军航空大学 基础基地基础部,吉林 长春 130022)
解多目标规划最小弱有效解的动约束组合同伦方法
何 非,商玉凤
(空军航空大学 基础基地基础部,吉林 长春 130022)
给出了解无界集上凸多目标规划问题最小弱有效解的动约束组合同伦方法,并证明了同伦路径的存在性和大范围收敛性。
多目标规划;凸规划;同伦算法;弱有效解;有效解
0引言
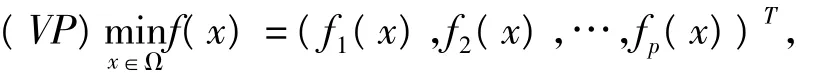
其中Ω={x∈Rn|g(x)=(g1(x),…,gm(x))T<0}称为可行集,
Ω={x∈Rn|g(x)=(g1(x),…,gm(x))T≤0}为严格可行集,
I(x)={i|gi(x)=0}为紧指标集。
定义1[1]设x*∈Ω,如果不存在x∈Ω,使得

则说x*是(VP)的有效解(或弱有效解)。
定理1[1]假设fj(x),gi(x)为凸函数(i=1,…,m),(j=1,…,p),且在∈Ω处可微,≥0(或>0)。如果存在∈Rm+,使得(满足条件:

考虑如下的多目标规划问题:
多目标规划问题的求解,一般都是通过主要目标法等形式转化为单目标规划来求解。文献[2](亦见文献[3~6])中,提出了解非凸Brouwer不动点问题和非凸规划问题组合同伦内点法,并在此条件下证明了同伦路径的存在性和大范围收敛性。利用组合同伦内点法,文献[7]给出了解多目标规划的直接算法。但该方法要求初始点为可行集的内点。文献[8]中给出了解凸规划问题的动边界组合同伦方法,该方法不要求可行集有界,初始点也不再限制为可行集内点。本文给出了解多目标规划问题的最小弱有效解的动约束组合同伦方法,同样不要求可行集有界以及初始点不限制为可行集内点。
1 假设条件及同伦方程的构造方法
在本文中总使用如下假设。
假设条件1
(A1)f,g∈Cl(l>2)且为凸函数;
(A2)Ω0非空;
为求解(1)构造动约束组合同伦方程



当t=1时,同伦方程变为

则同伦方程有唯一的解

当t=0时,同伦方程(2)变为方程(1)。
为方便作如下记号:

对于给定的w(0),将同伦方程(2)写为Hw(0)(w,t),并记它的的零点集记为H-1w(0)(0),即

命题1[9]设qi(x)(i=,1,…,l)是凸函数,且存在x∈Ωq。那么Ω0q非空的充要条件是:∀x∈∂Ωq,{▽qi(x),i∈Iq(x)}是正独立的。
即
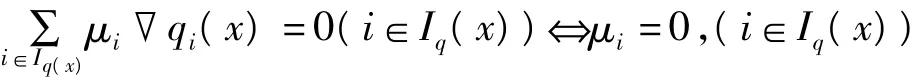
其中

下面我们证明在一定条件下同伦方程(2)的零点集包含一条起始于(w(0),1)的有界光滑曲线,当t→0时,曲线的另一端的极限点的(x,y)-分量(x*,y*)为问题(1)的解。

2 同伦路径的存在性及有界性
引理1 如果假设条件1成立,映射H由(2)定义.则对几乎所有的,0是
Hw(0)的正则值,并且H-1(0)包含一条起始于(w(0),1)的光滑曲线,记为Γ。证明 对任意的w(0)∈Rn×Rm++×Λ++×RP
++×{0},和T∈(0,1],

其中

这样我们有
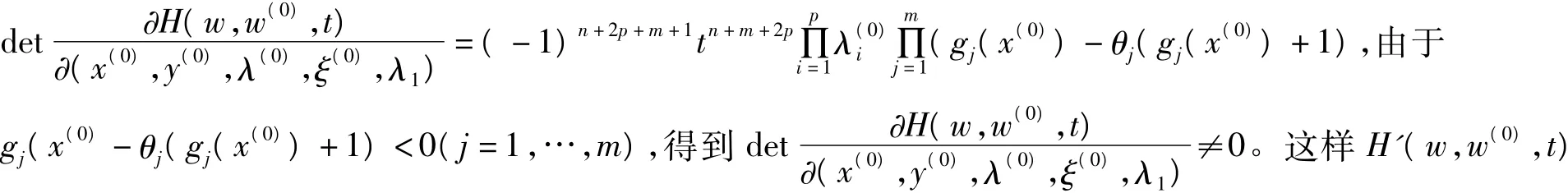
是行满秩的,即0是H(w,w(0),t)的正则值。由参数化的Sard定理得,对几乎所有的w(0),0是Hw(0)(w,t)的正则值,又由逆映像定理及Hw(0)(w(0),1)=0包含一条通过(w(0),1)的光滑曲线,记为Γ。
引理2 设如果假设条件1、2成立,映射H由(2)定义,则曲线Γ当t→0时极限点的x-分量有界。证明 假设存在Γ上的点列{(x(k),y(k),λ(k),ξ(k),hk,tk)}+∞k=1,满足当k→+∞时,‖x(k)‖→+∞。由是Γ上的点列,则有

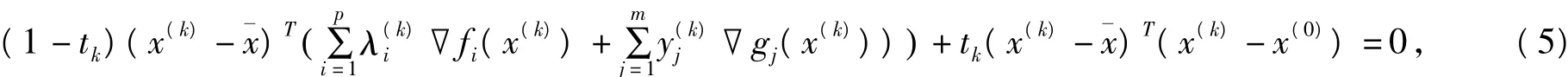
改写方程(5)为

由g(x(k))为凸函数,有

在(7)式两端同时右乘y(k),再结合(4),我们得到


于是


将(9)代入(6),得成立,这同假设条件2矛盾。
3 同伦路径的收敛性
定理1 设fi,gj∈Cl(l>2)(i=1,…,p),(j=1,…,m),假设条件1,2成立,映射H由(2)定义,则对几乎所有的,同伦方程的零点集(0)必包含一条经过点(w(0),1)的有界光滑曲线Γ,其另一端的极限点的(x,y)-分量(x*,y*)是(1)的解。
证明 由引理1我们知道存在一条经过(w(0),1)的光滑曲线Γ.设(w*,t*)是曲线Γ的另一端的极限点,则存在点列满足
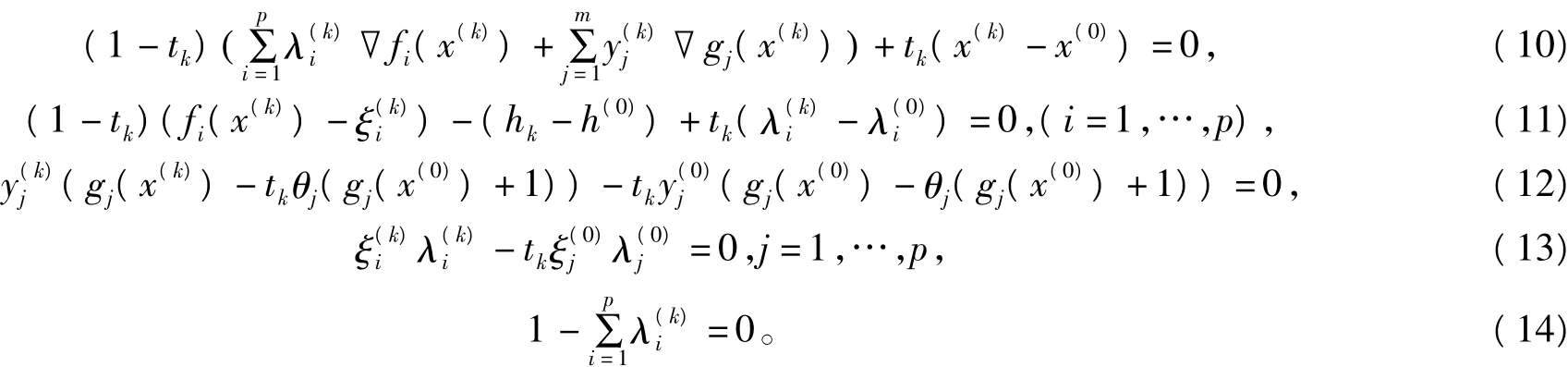
且(w(k),tk)→(w*,t*),由引理2得到当k→+∞时,‖x(k)‖→+∞,我们记x(k)的极限值为x*.由(14)我们得到0≤λ(k)i≤1(i=1,…,p),从而‖λ(k)‖→ +∞,并记λ(k)的极限值为λ*。
下面我们证明(hk,ξ(k),y(k))→+∞,分别讨论如下。
(1)hk→∞。
在(14)式的左右两端同乘λ(k),则有

结合(13-14)两式

得到

当k→∞时,右端极限存在且为有限值,因此hk→+∞。
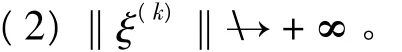

当t*<1时,
当t*=1时,
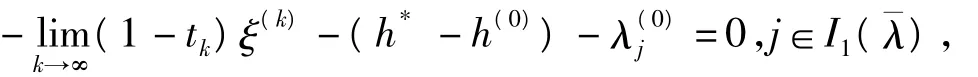
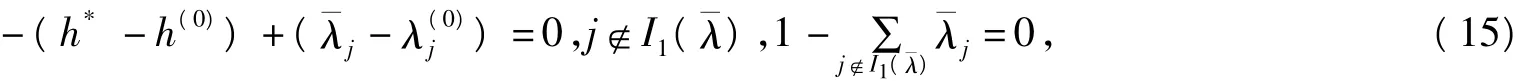

这是不可能的。
(3)‖y(k)‖→ +∞。
当t*=1时,由方程(10)式,

改写(16)为

若vj=0,∀j∈I(x*,1),当k→+∞时,方程(17)为

而由已知条件

得到x*≠x(0),这样vj≥0,(j∈I(x*,1))且不全为零。
当t*<1时,将(17)式整理为


这与命题1矛盾.综上可知当k→+∞时,曲线Γ是有界曲线,定理得证。
[1] 林锉云,董加礼.多目标优化的方法与理论[M].长春:吉林教育出版社,1992.
[2] Yu,B.,Lin,Z..Homotopy method for a class nonconvex Brouwer fixed point problems[J].Appl.Math.Comput.,1996,74:65-77.
[3] Feng,G.C.,Lin,Z.,Yu,B.Existence of an interior pathway of a Kraus-Kuhn-Tucker point of a nonlinear programming problem[J].Nonlinear Analysis Theory Methods Applications,1998,32:761-768.
[4] Feng,G.C.,Yu,B.Combined homotopy interior point method for nonlinear programming problems[J].Lecture Notes in Num.Anal.,1995,14:9-16.
[5] Lin,Z.H.,Li,Y.,Yu,B.A combined homotopy interior method for general nonlinear programming problems[J].Appl.Math.Comput.,1996,80:209-224.
[6] Lin,Z.H.,Yu,B.,Feng,G.C..A combined homotopy interior method for convex programming problem[J].Appl.Math.Comput.,1997,84:193-211.
[7] 刘庆怀,林正华.求解多目标规划最小弱有效解的同伦内点方法[J].应用数学学报,2000,23:188-195.
[8] 商玉凤,于波.凸规划问题的动边界组合同伦方法及其收敛性[J].吉林大学学报:理学版,2006,44:311-315.
[9] Rockefellar,T.Convex Analysis[M].Princeton:Princeton University Press,2000.
责任编辑:钟 声
Dynamic constraint combination homotopy method for minimal weak efficient solutions to multi-objective programming
HE Fei,SHANG Yu-feng
(Fundamental Department of Flight Training Base,Air Force Aviation University,Changchun 130022,China)
This article gives the dynamic constraint combination homotopy method for minimal weak efficient solutions to convex multiobjective programming problems on unbounded sets and proves the existence and convergence of the homotopy path.
multi-objective programming;convex programming;homotopy algorithm;weak efficient solution;efficient solution
O221.2
A
1009-3907(2010)08-0021-06
2010-06-05
何非(1982-),女,吉林辽源人,助教,硕士,主要从事最优化理论与算法研究。

