结构能量反应的振型分解法研究
常 磊, 叶献国
(合肥工业大学土木与水利工程学院,安徽合肥 230009)
基于能量的抗震设计方法是未来抗震设计的趋势之一,由于该方法能反应结构抵抗地面运动消耗地震能量,所以有很大的发展空间和潜力。但目前对结构耗能总体上还处于利用时程分析法计算能量反应的阶段,对地震动输入总体上是基于能量反应谱或强度指标等去评估地震破坏潜能。为建立结构能量反应与地震动能量特征间的关系,需要寻求任意 MDOF(Multi-Degree of Freedom)体系与SDOF(Single-Degree of Freedom)体系能量反应之间的关系。
有关振型分解理论应用在结构能量反应方程中的报道并不多。文献[1]虽是根据振型分解理论计算弹塑性体系的能量反应,但仍是基于结构运动方程的振型分解得出各振型的力和位移反应,考虑原结构的延性需求,进一步得出各振型的弹塑性SDOF体系,对各SDOF体系展开弹塑性时程分析,从而估计原结构的能量反应,并不是对结构能量反应方程进行振型分解。
本文通过理论推导,实现了MDOF体系能量反应方程的振型分解,得到各阶模态能量反应方程,提出模态能量的概念,原结构各能量反应则可表现为相应的各模态能量的叠加,从而实现了能量反应方程的振型分解。
1 能量反应方程
不失一般地,考虑地面运动下结构的运动方程,即
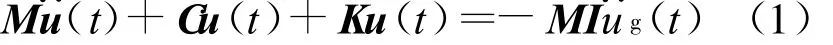
对du(t)在0~t0积分,可建立相对能量方程和绝对能量方程。相对能量方程为:

对应地记为:EK(t0)+ED(t0)+EH(t0)=EI(t0),各项分别为t0时刻的相对动能(简称动能)、阻尼耗能、滞回耗能以及相对输入能(简称输入能)。
绝对能量方程[2]可表述为:

2种能量表达式中阻尼能和总变形能是相同的,而动能和总输入能不同。严格地说,绝对能量方程更具有物理意义[2]。EI是以体系基础为参考,等效侧向力对体系所做的功(更适合长周期结构),而EIa表示基础剪力对基础位移做的功(更适合短周期结构),两者对于中等周期(卓越周期附近)非常接近。由于在计算(3)式时要用到地面运动速度时程﹒ug(t),一般情况下,地震波处理方法对计算结果的影响较大,不能从地面运动加速度积分而来,而(2)式的计算只需要地面运动的加速度即可,因而本文分析中采用相对能量反应方程,简称能量反应方程。
2 能量反应的振型分解
由于结构所有自振振型为完备正交系,体系的所有反应都可以用振型来展开,体系位移反应在任意时刻t的取值可由振型展开:

其中,假设结构总自由度数和总振型数分别为n和m,第i阶振型 Φi=(φ1iφ2i… φri…)T,振型广义坐标矢量q=(……)T。
记第i阶振型对结构总位移反应的贡献值为vi(t)=qi(t)Φi,并有振型正交性条件(假设阻尼也满足):

将(1)式对(dvi(t))T在0~t0积分得第 i阶振型下的能量方程为:

利用振型正交性条件可化简为:
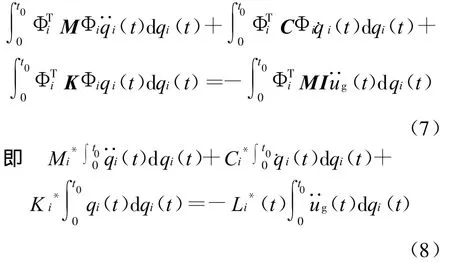
不妨简记为:
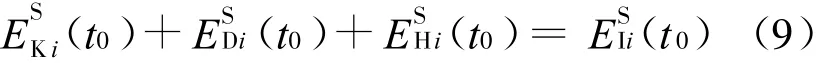
其中,各能量项分别表示t0时刻第i阶振型对结构动能、阻尼耗能、滞回耗能及输入能反应的贡献,记为第i阶模态动能、模态阻尼耗能、模态滞回耗能及模态输入能。
(6)~(9)式即为第i阶振型的能量方程,记为第i阶模态能量方程。由于振型广义坐标矢量q的各分量反应是独立的,因此各阶模态能量方程之间也是独立的。
将(4)式代入(2)式得,能量方程的振型广义坐标矢量表达形式为:
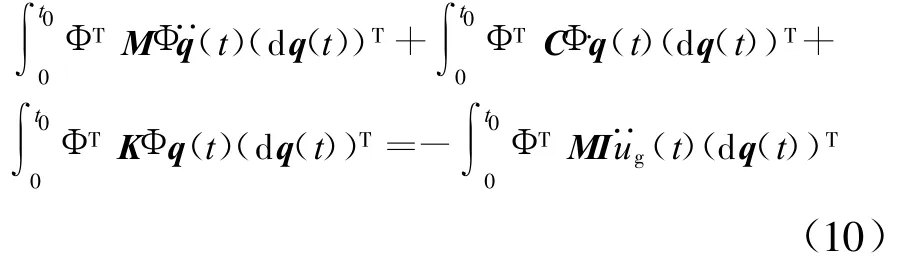
利用振型正交性,互换积分号和求和号,得:
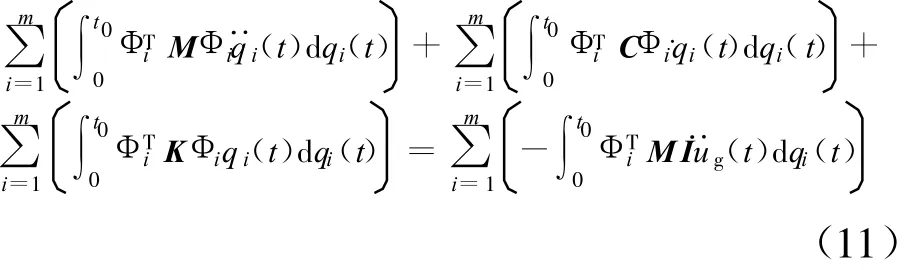
结合(6)~(9)式,(11)式可表示为:
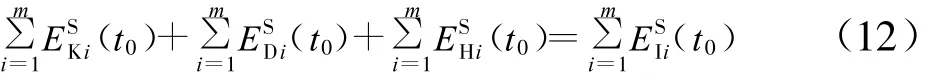
由于各阶模态能量方程之间是独立的,由(12)式可知,结构能量反应方程可以表示为各阶模态能量方程叠加,从而结构各能量反应也为各阶模态能量反应的叠加,即
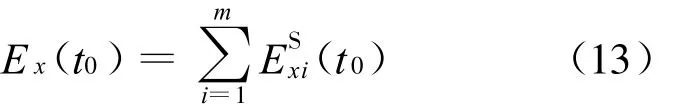
为方便叙述,将下标K、D 、H 、I代以 x(下同)。
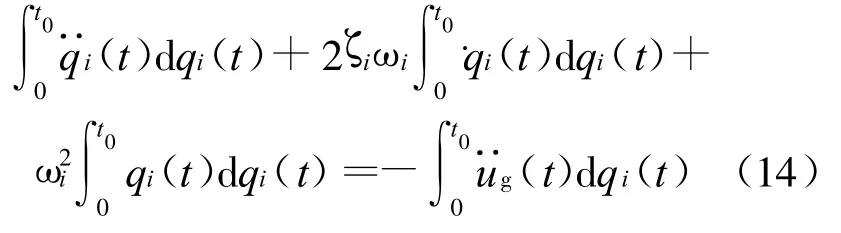
简记为:
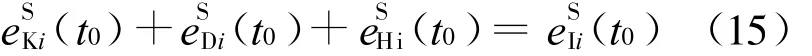
易证各阶模态能量反应与单位质量SDOF体系相应能量反应之间的关系为:

因此,(17)式可表示为:

与文献[4]提出的总输入能反应振型分解表达式相比较,(17)式不需对振型做一致化处理,表达更精简,引用时可消除表达上的误解[5]。同时(17)式对各能量反应均给出了一致的表达式,更具有物理意义,且可从能量角度反映Pushover中一些方法的合理性:
(1)利用有效振型质量将MDOF体系转化为等效SDOF体系,建立能力谱曲线[6,7]。
(2)结构运动多受第1阶振型控制,这反映在第1阶振型的有效振型质量较大,其能量反应对结构的贡献占主导地位(下述实例可证实这一点),因此在Pushover分析中很多结构可按第1阶振型的荷载分布模式加载,应用广泛。
(3)考虑足够多的结构振型,并取各自振型向量为荷载分布模式,做相应振型下的Pushover分析,再考虑某种组合原则对各分析结果进行组合,即MPA法。文献[8]指出,若结构体系为线弹性,并取结构所有振型进行分析并组合,其结果与振型分解反应谱法计算的结果相同。
3 算例分析
验算结构为10层的框架结构,阻尼设为Rayleigh阻尼,取一、二阶阻尼比均为0.02,结构质量和刚度特性见表1所列,模态特性见表2所列。

表1 结构特性

表2 结构模态特性
取1940年美国Imperial Valley Earthquake记录之一的南北分量,其峰值的加速度为341.7 cm/s2作为地震输入。按本文提出的能量反应方程的振型分解方法,分别计算各振型下的各模态能量,如图1所示,再按照(17)式叠加各模态能量得出结构相应的能量反应,按照原结构运动方程利用Canny程序[9]展开弹性时程分析,计算其能量反应,如图2所示。
由图1可见,能量在各模态间总体分布特征为:随阶数增加,模态能量依次减小,且第1阶模态能量占主导地位。各阶模态能量反应差距悬殊,尤其是前 4阶,随着阶数增加,能量按0.1倍量级递减。
从图2来看,按照振型分解后的能量结果与Canny按原结构计算结果非常相近,时程曲线几乎重合,说明本文提出的方法是正确的。

图1 各阶模态能量计算结果

图2 能量计算结果对比
4 结束语
本文利用振型分解理论,实现了对弹性体系的能量反应方程的振型分解,提出了模态能量的概念,指出结构能量反应方程可以表示为各阶模态能量方程的叠加,结构各能量反应也为各阶模态能量反应的叠加,并给出了总能量反应与单位质量SDOF体系相应能量反应间的关系式为算例表明随阶数增加模态能量总体上依次减小,且各阶模态能量反应差距悬殊,第1阶模态能量占主导地位。按照能量振型分解法计算的能量反应与原结构的能量反应几乎一致,说明能量反应的振型分解法的正确性。但此方法仅限于结构的弹性反应,对非弹性下反应,其适用性有待验证。
[1] 翟希梅,吴知丰.多层结构能量计算的振型分解方法[J].哈尔滨工业大学学报,1998,30(1):121-124.
[2] Uang C M,Bertero V V.Evaluation of seismic energy in structures[J].Earthquake Engineering&Structural Dynamics,1990,19(1):77-90.
[3] Chopra A K,Goel R K.A modal pushover analysis procedure for estimating seismic demands for buildings[J].Earthquake Engineering & Structural Dynamics,2002,31(3):561-582.
[4] 程光煜,叶列平.弹性多自由度系统地震输入能量的研究[J].工程抗震与加固改造,2006,28(4):6-17.
[5] 周 云,乐 登,邓雪松.设计用地震动总输入能量谱研究[J].工程抗震与加固改造,2008,30(5):1-7.
[6] 刘金龙.能力谱方法在模态 Pushover分析中的应用[J].沈阳建筑大学学报:自然科学版,2009,25(1):90-94.
[7] 王 丰,李宏男.多维结构地震位移反应的近似估计[J].多维能力谱法振动工程学报,2006,19(2):270-276.
[8] Chopra A K.Dynamics of structures:theory and applications to earthquake engineering[M].北京:清华大学出版社,2005:508-532.
[9] Li Kangning.CANN Y technical manual[M].Singapore:Canny Consultant Pte Ltd,2009:246-281.

