非参数回归模型的贝叶斯局部线性估计

龙杏芬,张德生,武新乾

非参数回归模型的贝叶斯局部线性估计

龙杏芬1,张德生1,武新乾2

(1.西安理工大学理学院,陕西西安710054;2.河南科技大学理学院,河南洛阳471003)

对于非参数回归模型^y=m(x)+ε,在局部线性估计中窗宽h的先验分布为Gamma分布的条件下,用未知光滑函数m(x)的后验均值构造了它的贝叶斯估计,并给出了参数的后验分布和抽样方法.模拟算例证明了贝叶斯局部线性估计方法的可行性.

窗宽;局部线性估计;贝叶斯方法;Gibbs抽样方法

考虑非参数回归模型

其中x∈R为固定设计变量,m(x)是未知光滑函数,ε为随机误差,它反映了除解释变量外其他影响被解释变量的可观察或不可观察的因素对被解释变量的影响以及模型的设定误差等.

对m(x)的估计已有丰富的研究成果,如:柴根象和洪圣岩[1]、Fan和Yao[2].其中,局部线性估计是一种重要的、常用的估计方法,但是,使用该方法的一个关键问题是窗宽h的选择.对于固定窗宽,当h太大时,会得到过度光滑的曲线,产生一个很大的模型偏差;当h太小时,会造成过度拟合数据,即除了数据点外其他点的函数值均为零[3].对于变窗宽,需掌握解释变量的分布信息以改进估计的效率[4].近年来,一些学者提出了窗宽选择的贝叶斯方法.如:欧祖军[3]基于贝叶斯方法研究了m(x)的局部多项式估计,但他考虑的是小区间个数和结点位置为随机变量的情形.其他估计方法还有卢一强和茆诗松[5]等.Crainiceanu C等[6]给出了罚样条回归的Bayes统计分析.

本文将窗宽h看作随机变量,基于贝叶斯方法构造了m(x)的局部线性估计,给出了有关参数的后验分布和抽样方法.

1 贝叶斯局部线性估计

局部线性估计为最小化

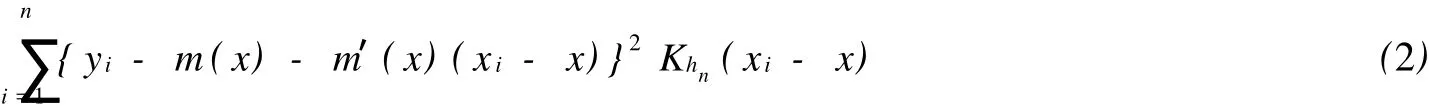
其中,Kh(u)=h-1K(h-1u)为概率密度函数.m(x)的局部线性估计等价于落在[x-h,x+h]上的xi和与其对应的yi的模型

即

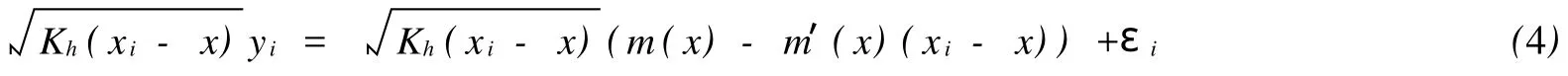
的最小二乘估计.m(x)的局部线性估计的矩阵表示为

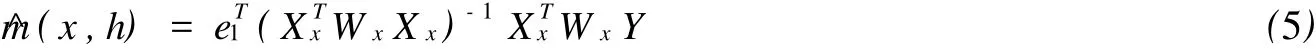
其中 e1=(1,0)T,Xx=(Xx,1,…,Xx,n)T,Xx,i=(1,(xi-x))T,

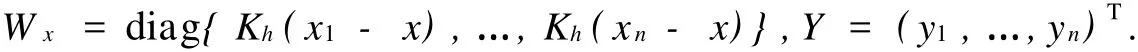
对于模型(4),假定εi为独立同分布误差,服从N(0,σ2),观察数据D=(xi,yi)ni=1.记β=(m(x),m′(x))T,(β,σ2)为给定h之后的参数向量,选择h的先验分布为P(h),参数(β,σ2)的先验分布为P(β,σ2|h),用β的后验均值构造它的贝叶斯估计.由随机变量的贝叶斯公式[7],参数向量(β,σ2)的联合后验分布与下式成比例,即

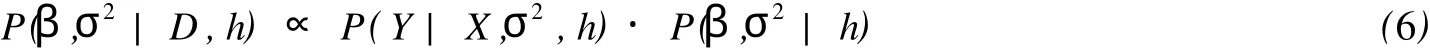
本文的主要结果如下.

定理1 给定h,K(·)是概率密度函数,如果取(β,σ2)的先验分布为无信息的先验分布P(β,σ2|h)∝,则(β,σ2)的后验分布为正态倒伽马分布

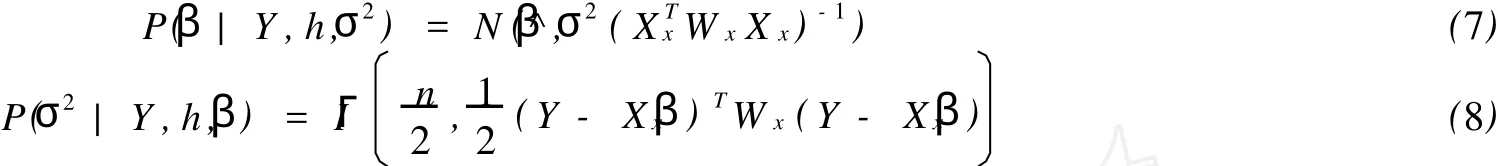
证明 由假设εi～N(0,σ2)且独立同分布,有

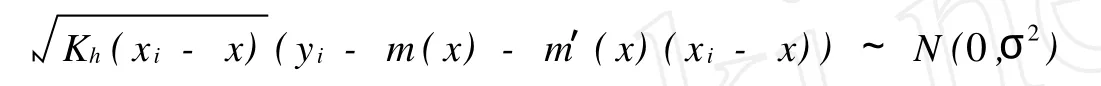
所以,似然函数为

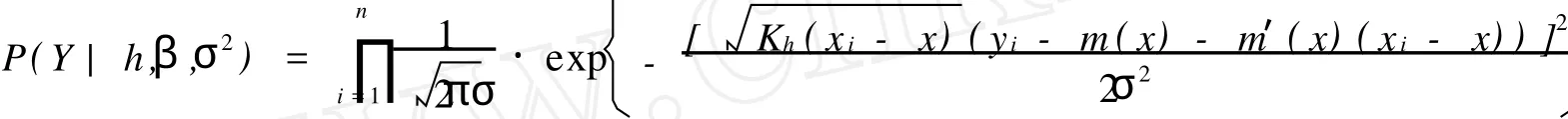
由式(6),(β,σ2)的联合后验分布与下式成比例

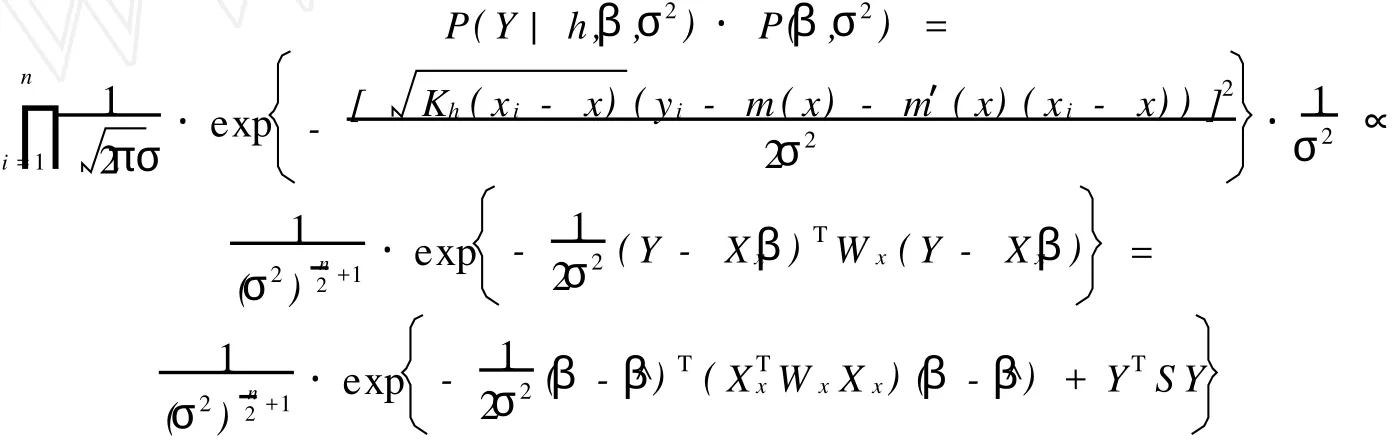
其中 ^β=(XTWxX)-1XTxWxY,S=Wx-WTxXx(XTxWxXx)-1XTxWx.

给定h,参数β,σ2的联合后验分布与上式成正比.所以,β,σ2的后验分布分别为:

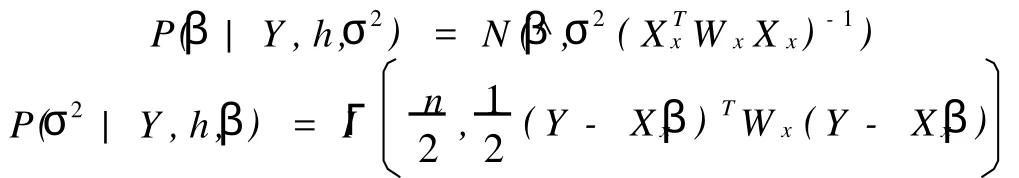
证毕.

推论1 在定理1的条件下,取h的先验分布为P(h),根据随机变量的贝叶斯公式[7],h的后验分布如下式:

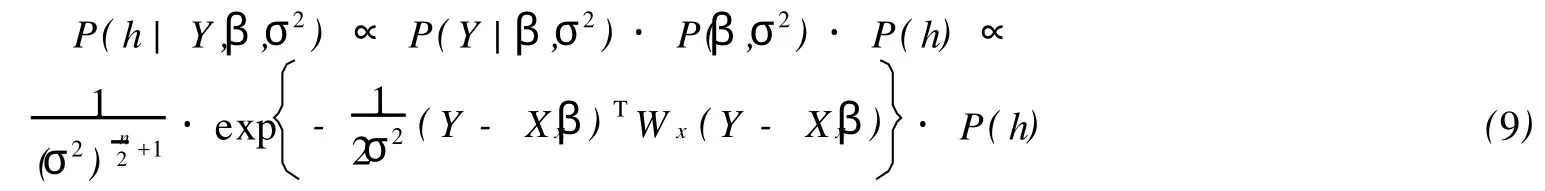
证明 同定理1,此处从略.

注1 从形式上看,参数β的贝叶斯估计与其最小二乘估计量完全相同,但二者有着根本不同的含义[8]:此处β是随机变量,其后验均值^β是一个具体的数;而在经典统计推断理论体系中,β只是未知参数,不具有随机性,其最小二乘估计^β是随机变量.

注2 由定理1可知:给定h,参数β,σ2的后验分布是简单的,但h的后验分布是比较复杂的,不存在解析表达式.在式(9)中,令,应用如下的筛选技术[9]:虽然h的后验分布表达式比较复杂,但可以找到G (h)的一个上界,即存在一个常数c,使得G(h)≤c,此时,P(h|Y,β,σ2)≤ecP(h)对一切h均成立.然后,再根据P(h)抽样,若满足一定条件就作为来自满条件后验分布的样本.

特别的,类似于定理1和推论1的证明可得:

定理2 取定h,若K(·)是[-1,1]上的均匀分布的概率密度函数K0(·),取(β,σ2)的先验分布为无信息的先验分布P(β,σ2|h)∝.则(β,σ2)的后验分布为正态倒伽马分布:

推论2 在定理2的条件下,取h的先验分布为P(h),根据随机变量的贝叶斯公式[7],h的后验分布如下式:

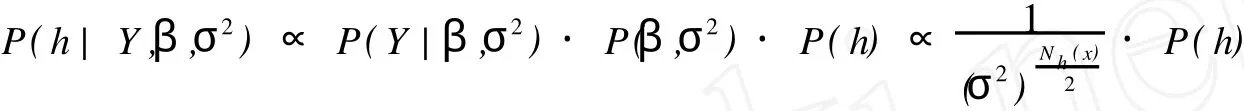
2 计算方法

为了方便计算,记θ=(β,σ2,h),θ的更新过程是一个Gibbs抽样[5]过程.下面给出算法:

(1)确定β,σ2,h的初值,即θ0=(β0,σ2(0),h0);

(2)根据P(β|Y,hk,σ2(k))抽取βk+1;

(3)根据P(σ2|Y,βk+1,hk)抽取σ2(k+1);

(4)根据P(h|Y,βk+1,σ2(k+1))抽取hk+1;

(5)生成θk+1=(βk+1,σ2(k+1),hk+1),

这样,就得到了一个收敛于(β,σ2,h)的后验分布式的序列.舍去前有限项,用留下的项作为样本计算样本均值来估计β.

3 数值模拟

例 解释变量为确定性变量,随机误差项{ui}独立同分布.模拟的模型为Yi=sin(2exp(Xi+1))+ui,让Xi在[0,1]上取值,Xi=,i=1,…,120,ui～N(0,0.25),i=1,…,120.取h的先验分布为p(h)=G (8,100),P(β,σ2)∝,σ2(0)=0.25,h(0)=0.08,k=1 000,核函数选用抛物线核K(u)=0.75(1-u2)+.得到样本后,舍去前700项,用后300项,每隔10个取一个用于数据分析,得到30个后验样本.计算后验均值得到m(x)的估计如下图1,图2为不变窗宽局部线性估计(h=0.08).

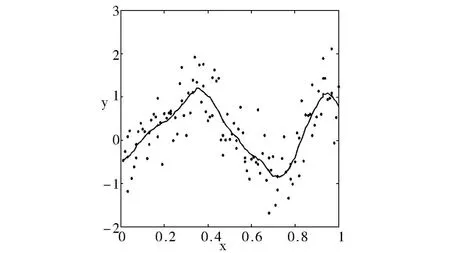
图1 m(x)的贝叶斯估计Fig.1 Bayesian estimator ofm(x)

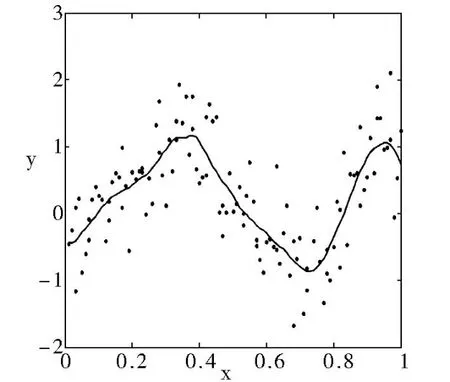
图2 m(x)的局部线形估计Fig.2 Local linear estimator ofm(x)

表1 贝叶斯估计和局部线性估计的MS E和R2Table 1 MSEandR2of Bayesian estimator and Local linear estimator

由表1可以看出贝叶斯估计同局部线性估计相比较,残差平方和及均方差较小,而拟合优度有所提高.从本例可以看出:当不易选择窗宽h时,使用贝叶斯方法也能得到m(x)的较好的估计.

4 结论

本文基于非参数回归模型的局部线性估计方法和贝叶斯理论,构造了一元非参数回归模型的贝叶斯估计,用m(x)的后验均值构造了它的贝叶斯估计,同时给出了参数的后验分布和抽样方法.模拟算例证明了贝叶斯估计的可行性.

[1] 柴根象,洪圣岩.半参数回归模型[M].合肥:安徽教育出版社,1995.

[2] FAN J,YAO Q.Nonlinear Time Series:Nonparametric and Parametric Methods[M].New York:Springer-Verlag.

[3] 欧祖军.基于Bayes方法的非参数估计[D].南京:东南大学,2005.1.

[4] 叶阿忠.非参数计量经济学[M].天津:南开大学出版社,2003.

[5] 卢一强,茆诗松.非参数Bayes样条回归[J].华东师范大学学报(自然科学版),2004,12(4):33-39.

[6] CRAINICEANU C,RUPPERT D,WANG M P.Bayesian Analysis for Penalized Spline Regression Using WinBUGS.[J]. Journal of Statistical Sof tware,2005,31(3):1-24.

[7] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,2006.

[8] 朱慧明,韩玉启,等.贝叶斯多元统计推断理论[M].北京:科学出版社,2006.

[9] 髙惠璇.统计计算[M].北京:北京大学出版社,1995.

[10] 田亚爱,田 铮,武新乾,等.具有非参数AR(1)误差的回归模型的局部线性估计[J].工程数学学报,2008,4(2):253-259.

[11] 王 琳.非参数局部线性估计方法及对中国股市杠杆效应的实证分析[J].大众科技,2008,5(5):185-187.

Bayesian Local Linear Estimation for Nonparametric Regression Model

LONG Xing-fen1,ZHANG De-sheng1,WU Xin-qian2
(1.School of Science,Xi’an University ofTechnology,Xi’an710054,China; 2.School of Science,Henan University of Science and Technology,L uoyang471003,China)

The nonparametric regression model^y=m(x)+εis considered,wherem(x)is a smooth function.Bayesian local linear estimator of nonparametric functionm(x)is constructed by the average of samples from posterior distribution under the prior distribution of bandwidthhfollows Gamma distribution. Posterior distribution of parameters and a sampling method are also given.An example is simulated to show the feasibility of the method.

bandwidth;local linear estimation;Bayesian method;Gibbs sampling

O212.8

A

0253-2395(2010)03-0371-04

2009-09-21;

2009-10-28

国家自然科学基金(50779055)

龙杏芬(1984-),女,山西长治人,硕士研究生,研究领域为应用概率统计.E-mail:duijiaojuzhen@163.com