矢量波动方程的时空高阶方法
赵艳敏,何沧平
矢量波动方程的时空高阶方法
赵艳敏1,何沧平2,3
(1.许昌学院数学科学学院,河南许昌461000; 2.中国科学院数学与系统科学研究院计算数学与科学工程计算研究所,北京100190;3.中国科学院研究生院,北京100190)
文章将Gauss-Lobatto-Legendre多项式的高阶矢量谱元方法应用于矢量波动方程.由于矢量波动方程可以表示为一个无穷维Hamilton系统且经空间上的有限元方法离散后是一有限维Hamilton系统,利用4阶辛分块的Runge-Kutta方法来求解该有限维Hamilton系统,以期保持系统整体的能量和结构.
矢量波动方程;矢量谱元方法;Hamilton系统;辛分块的Runge-Kutta方法
0 引言
由于电磁场计算对生物电磁学、医学、微波遥感、通讯技术和纳米电子学等众多领域的重要影响,对电磁场问题如何设计数值算法成了人们越来越关注的课题.矢量波动方程就是其中重要的一类.求解此类方程,工程界用得比较多的方法是有限差分方法[1-3].随后,有限元方法凭借其区域灵活性优势也越来越多地被应用于计算电磁场问题[4-7].最近,柳清伙等学者又提出了利用谱元方法与传统的Runge-Kutta方法相结合来求解时域Maxwell方程[5].矢量波动方程可以表示成一个无穷维Hamilton系统,因此它的解可以看做是泛函空间的Hamilton流,它在时间方向上是保整体能量和辛结构的.辛方法是唯一能精确保持连续Hamilton流内在性质的数值方法.基于此优势,辛算法是求解由无穷维Hamilton系统通过离散方法降维而成的有限维Hamilton系统的首选[8-13].本文对于矢量波动方程,给出了其在空间上经基于Gauss-Lobatto-Legendre多项式的高阶谱元方法离散后的有限维Hamilton系统;并给出了在时间方向上全离散求解该有限维系统的高阶辛方法-辛分块的Runge-Kutta方法.本文的内容安排如下:第一节,给出了矢量波动方程及其无穷维Hamilton形式,并对空间半离散后的系统进行分析;第二节,给出了空间离散所采用的高阶矢量谱元方法及刚度矩阵、质量矩阵的一些计算技巧;第三节是对本文内容的总结.
1 矢量波动方程和高阶辛算法
在各向同性、非耗散的线性介质中,考虑如下矢量波动方程:

其中ε和μ分别是介质的介电常数和磁导率.
设p为标量,q=(q1,q2)为向量,则有

引入变量F,(1)可以改写为:

为简单起见,设ε,μ为常数,我们考虑的区域Ω中有有限种介质.上述矢量波动方程可以表示为如下无穷维的Hamilton系统:

在空间方向,(2)式的弱形式为:找E,F∈H0(curl),∀W∈H0(curl)使得
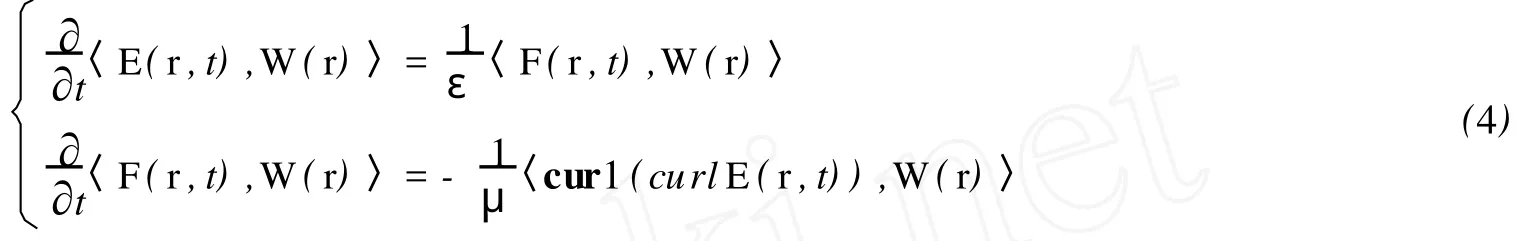
其中〈U,W〉=∫ΩU·WdΩ;H0(curl)={v∈(L2(Ω))2;curlv∈L2(Ω),n×v|∂Ω=0}.令Γh为区域Ω的矩形正则剖分.设^K是ε-η平面的参考元,对剖分Γh而言,对于任意的K∈Γh,存在一个可逆映射FK:^K→K.
令Φi,i=1,2,…,Ne为^K上的基函数.相应的有限元空间为(在第二节中,我们给出具体的有限元空间):

相应的离散问题是:对于(4),找E,F∈Vh,对任意的¯Φj∈Vh,使得
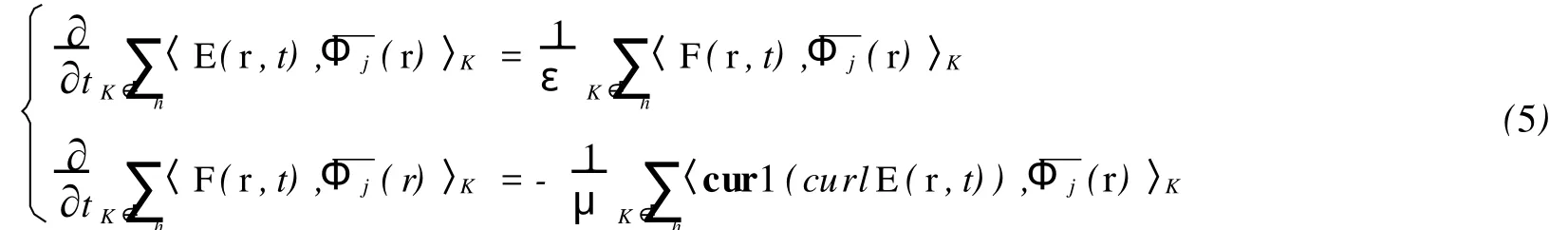
显然,在K上,E,F可以由基函数线性表出:

将它们代入(5)式,可得其矩阵形式:



总体质量矩阵M和总体刚度矩阵S分别由单元质量矩阵M(e)和单元刚度矩阵S(e)按照总体自由度编码构成,其中M(e)和S(e)的元素为:
其中

由于原方程经有限元离散后为一有限维Hamilton系统,我们用4阶显式辛分块的Runge-Kutta (SPRK)方法对式(7)进行全离散求解.s阶辛分块的Runge-Kutta(SPRK)方法的系数可由图1给出.

图1 S阶辛块Runge-Kutta方法的Butcher表Fig.1 Table of Butcher for SPRK method
通常,它应用于常微分方程

结果为:
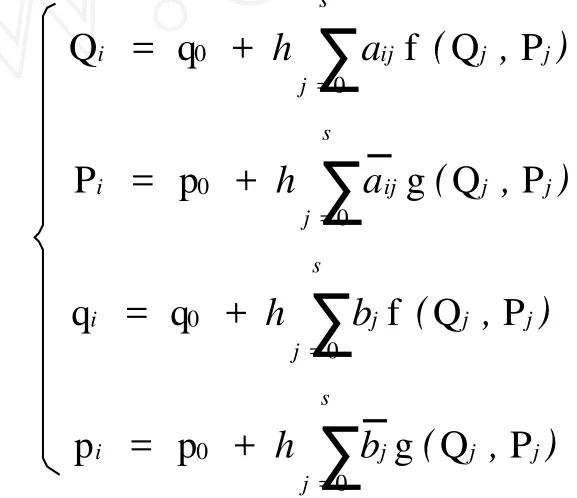
PRK方法的辛条件是:

(7)式是一个可分系统,故PRK方法的辛条件仅有(8)式.
特别地,4阶显式分块Runge-Kutta(SPRK)方法的Butcher表见图2,其中γ1=

图2 4阶辛分块Runge-Kutta方法的Butcher表Fig.2 Table of Butcher for 4th-order symplectic SPRK method
2 高阶矢量谱元方法
我们采用基于N阶Gauss-Lobatto-Legendre(GLL)多项式的矢量谱元来离散矢量波动方程.在第一节中可以看到,最后用辛方法求解方程(7)时,涉及的只是通过有限元离散后得到的总体质量矩阵和总体刚度矩阵.在本节中,我们介绍矢量的GLL谱元方法并在保证逼近精度的前提下,利用一些技巧在求总体质量矩阵和总体刚度矩阵及其逆矩阵时,尽可能地减少计算量.
N阶Legendre多项式是

GLL点{ξj,j=0,1,…,N}是多项式(1-ξ2)L′N(ξ)的零点.
在参考元[-1,1]上,N阶GLL基函数为:

显然有φj(ξk)=δjk,∀j,k=0,…,N.
在(7)式中,我们令Φi=Φξi+Φηi,其中Φξi=Φξrs=ξ^ φr(ξ)φs(η);Φηi=Φηrs=η^ φr(ξ)φs(η).
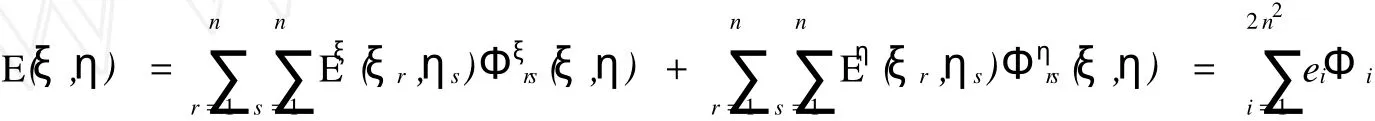
下面给出S(e),M(e)的具体表达.为了计算方便,我们将S(e)进行分块处理:S(e)=[A B;C D]
各块的元素分别为:
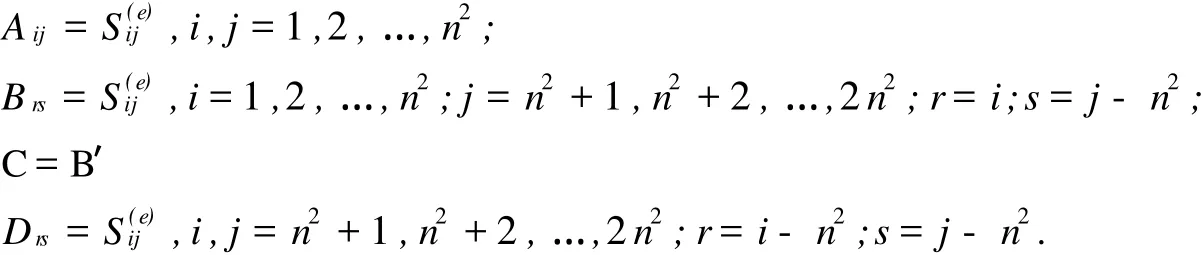
计算过程中,我们将用到GLL多项式φj在第i个GLL点的导数值,它即是矩阵~D的元素¯Dij:
令n=N+1,在参考元[-1,1]×[-1,1]上,我们易得:
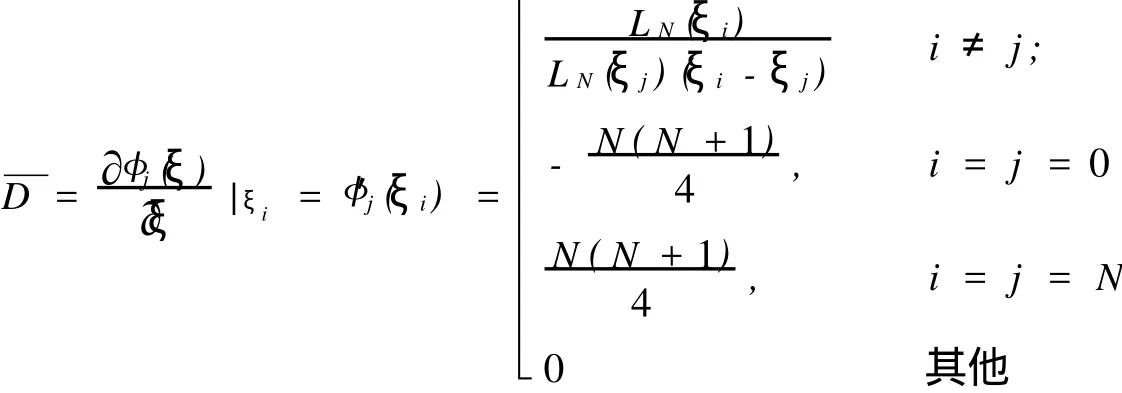
为了节省计算时间、减少计算量,我们将采用一些技巧使得S(e),M(e)对角或块对角.我们以矩阵A和M(e)的计算为例来展示:
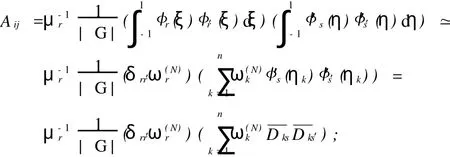
单元质量矩阵M(e)的元素为
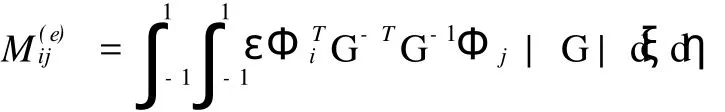
设K是矩形单元,则Jacobi阵G是一对角阵,即G=diag(g11,g22).
根据我们的自由度编码,以i,j∈[1,n2]为例,即Φi=^ξ φr(ξ)φs(η),Φj=^ξ φr′(ξ)φs′(η),处理M(e)的过程如下:

S(e),M(e)已求出,则按照总体自由度编码以及总体自由度与单元自由度的对照关系,容易得到总体刚度矩阵S及其逆阵S-1和质量阵M及其逆阵M-1.最后,利用第一节中所述的4阶辛分块的Runge-Kutta方法即得方程(7)全离散解.
3 总结
本文利用基于GLL多项式的矢量谱元空间离散方法结合时间方向上的辛离散方法来求解矢量波动方程.充分利用了谱元方法的高精度特点,并采用了一些数值处理技巧降低计算量从而解决了高阶方法计算量大的问题;注意到矢量波动方程谱元半离散后的系统的结构特点,文中采用的高阶辛格式在保证解精度的前提下,保持了系统整体的能量和结构.
[1] YEE K S.Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media[J]. I EEE Trans A nte Prop,1966,14:302-307.
[2] TAFLOVE A,HAGNESS S C.Computational Electrodynamics:The Finite-Difference Time-Domain Method3rd[M].Boston:A rtech House,2005,Boston.
[3] SHA W,HUANG Z X,WU X L,CHEN M S.Application of the Symplectic Finite-Difference Time-Domain Scheme to Electromagneticsimulation[J].J Comput Phys,2007,225:33-50.
[4] MONK P B.Analysis of A Finite Element Method for Maxwell’s Equations[J].S IA M J N umer A nal,1992,29:714-729.
[5] LIU Y X,L EEJ H,XIAO T,LIU Q H.A Spectral-Element Time-Domain Solution of Maxwell’s Equations[J].MicroOpti Technol Lett,2006,48:673-680.
[6] RIEBEN R,WHITE D,RODRIGUE G.High-Order Symplectic Integration Methods for Finite Element Solutions to Time Dependent Maxwell’s Equations[J].I EEE Trans A nte Prop,2004,52:2190-2198.
[7] J IAO D,J IN J M.Three-Dimensional Orthogonal Vector Basis Functions for Time-Domain Finite Element Solution of Vector Wave Equations[J].I EEE Trans on A nte and Prop,2003,51:59-66.
[8] FENG K.Collected Works of Feng Kang(II)[M].Beijing:National Defense Industry Press,1995.
[9] QIN M Z,ZHU W J.Construction of Higher Order Symplectic Schemes by Composition[J].Computing,1992,47:309-321.
[10] LU X W,SCHMID R.A Symplectic Algorithm for Wave Equation[J].Math Comput Simul,1997,43:29-38.
[11] TANG Y F,CAO J W,LIU X T,SUN Y C.Symplectic Methods for the Ablowitz-Ladik Discrete Nonlinear Schrödinger Equation[J].J Phys A:Math Theor,2007,40:2425-2437.
[12] SUN G.Construction of High Order Symplectic Runge-Kutta Methods[J].J Comput Math,1993,11:250-260.
[13] ZHAO Y M,DAI G D,TANG Y F,LIU Q H.Symplectic Discretization for Spectral Element Solution of Maxwell’s E-quations[J].J Phys A:Math Theor,2009,42:325203.
Time-Domain High-Order Method for Vector Wave Equation
ZHAO Yan-min1,HE Cang-ping2,3
(1.School of Mathematical Sciences,Xuchang University,Xuchang461000,China; 2.L S EC,ICMS EC,Academy of Mathematics&S ystems Science,Chinese Academy of Sciences,Beijing100190,China; 3.Graduate School of Chinese Academy of Sciences,Beijing100190,China)
The high-order vector SEM based on Gauss-Lobatto-Legendre(GLL)polynomials is applied to vector wave equation.Since the vector wave equation can be denoted as an infinite-dimensional Hamiltonian system which will become a finite-dimensional Hamiltonian system by the finite element discretization on spatial direction,we adopt 4th-order symplectic partitioned Runge-Kutta(SPRK)method to solve the finitedimensional Hamiltonian system for conserving total energy and structure of the system.
vector wave equation;vector spectral element method;Hamiltonian system;symplectic partitioned Runge-Kutta method
O241
A
0253-2395(2010)03-0329-06
2010-01-11
国家自然科学基金(10672143;10872037);河南省教育厅自然科学基金(2009A110017)
赵艳敏(1979-),女,讲师,博士,研究领域:辛算法、有限元理论及其应用.E-mail:zhaoym@lsec.cc.ac.cn

