一种基于RANSAC框架的椭球提取算法

程志全， 叶永凯， 李 宝

（国防科学技术大学计算机学院，湖南 长沙 410073）

将数据采集设备获取的实物样件数据进行处理和三维重构，反求工程在计算机上复现实物样件的几何形状，并在此基础上进行原样复制、修改或重设计，在工程实验、计算机图形和计算机辅助几何设计等方面有着广泛的应用。其中，如何从扫描得到的离散数据（通常为点云模型）中提取原始模型外表的几何基元（多为二次曲面），是对模型进行各种处理的基础的、关键性的工作。基元提取拟合给定点云模型的最佳二次曲面，用点云与提取出的二次曲面之间的“最小距离”对拟合性能进行评价，以确定拟合曲面是否真正充分表达了整个模型[1]。当前各基元提取算法多针对平面、球、圆柱、圆锥和可扩展曲面等相对简单的二次曲面，很少涉及椭球等复杂的基元[2-3]。面向几何基元提取问题，本文提出了一种从点云模型中有效提取复杂椭球的算法。

1 相关工作

基元几何基元的检测和提取一直备受研究人员的关注。多年来，有大量不同的方法被提出，限于篇幅，本文将不在此对这些方法进行详细地讨论，仅对一些最重要的方法做一个简要的回顾。

RANSAC（RANdom SAmpling Consensus，随机采样一致性）[2]和Hough变换是用于几何基元提取的最常用的两种方法。有大量的噪声和外点的情况下，二者都被证明能成功地检测出二维和三维空间的形状，但是低效和高存储容量要求是它们的主要缺点。为此，COHEN-STEINER等[3]提供了一个通用的变分框架，使用多个平面来逼近表面。WU等[4]将此方法进行了扩展，使用一组更加复杂的基元（平面、球面和可扩展的圆环）来逼近表面。他们的目标不仅仅是检测几何基元，而且还试图寻找给定基元数目时的全局最优表示。RUWEN等[2,5]增加基元的类型（平面、球体、圆柱、圆锥和圆环），并提出了一种高性能的 RANSAC算法，能在提取不同类型的基元形状的同时，保持基本 RANSAC算法框架的良好特性，如一般性和简洁性。椭球可以看作广义圆柱体的一个特例，具有一定的对称性，相对于球也能更灵活地表现较复杂的几何信息。本文基于文献[2]中的算法框架，实现点云中椭球基元的有效检测与提取。

2 点云模型的椭球体提取

本文采用RANSAC框架（伪代码见图1）完成椭球的提取工作：使用一种局部的采样策略进行采样[2]，从点云数据（点数为 N）中随机选取最小点集，即能唯一地确定椭球的最少数目的点的集合，本文设点数为6（2.1节）；利用最小二乘的方法计算椭球的参数，即椭球的中心、半轴长和偏转角度（2.2节）；基于距离和偏角参数验证求得的椭球的正确性（2.3节）；将通过验证的椭球与点云中的所有点进行匹配，以判断有多少点可以由此候选点基元近似表示，点的数目被称作分数，完成了分数函数（2.4节）的计算，得到了评估椭球的方法，最后依据分数方程筛选出最好的候选点m。这个最佳的候选点只有在这种情况下才会被接受：由m中点的个数|m|和已经选出的候选点形状的个数得到的能正确检测出形状的置信概率大于用户定义的阈值pt。进而通过求投影点的方法绘制出检测到的椭球。如果一个候选点被接受，那么相应的点会从点云中删除，并这个候选也会从集合 C中删除。算法在概率大于pt的时候停止，其中τ是用户定义的最小的形状包含的点的数目，这表明所包含的点超过τ的形状已经被检测出来的概率大于pt。算法用了一种标准的分数方程来计算一个候选点能容许的点的数目，即RANSAC算法所说的一致集。分数方程的输入包括评估的候选形状的参数，以及有两个用户定义的阈值ε和α：ε表示一个能容许的点到候选形状的最大距离；α是一个点的法向到候选形状的法向的最大偏移量。综上所述，在检测开始前，用户需要定义以下的阈值：计算分数方程时的距离阈值ε、角度阈值α、最小的椭球包含的点的个数τ和置信概率阈值pt。

对于置信概率，我们假设任意6个点都可以产生一个候选点，那么一次能够正确检测到形状的概率是

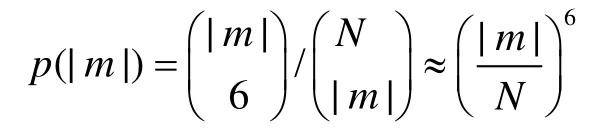
在选出了|C|个候选点之后可以正确的检测出形状的概率是

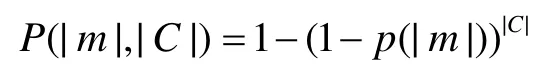
2.1 局部采样

在进行采样时，本文采用局部的采样策略进行采样[2]，使用一个八叉树来有效地建立样本点间的空间近似度。当要选择样本点来产生新的候选点时，首先没有任何约束地从空间中选出一个点，然后从八叉树中任意一级随机选择一个包含该点的单元格，其他的5个点从这个单元格内选出。

2.2 椭球的估计

椭球的估计是指从上面采样的点中产生一个与点云中实际隐藏的椭球相近的一个椭球模型。椭球面的参数化方程如下

要解出这个方程中A到I这9个参数，需要在椭球面上的9个点，将这9个点带入到公式(1)中，问题就变成了一个解线性方程组的问题了。而实际上，因为不能保证所抽取的样本点都在椭球面上，就算有9个样本点的数据，构成一个线性的方程组，这个方程组也可能无法解出这9个参数。本文利用椭球的几何性质，先估计出椭球的中心，然后用最小二乘方法计算出椭球的轴长和偏转角度。

椭球中心的估算方法的基础为椭球中心的求解引理《空间解析几何》[6]：对于椭球上的 4个不共面点和p4，任两个点的中心和两个点的椭球切平面相交所得的直线建立平面Pi，所有Pi相交于椭球的中心点。任取4个带法向的点，建立相应的平面Pi(i=1,…4)，平面方程为：。因为这4个点不一定在椭球面上，所以从中任取4个平面不一定交于一点。因此，本文选择距离这4个平面的距离平方之和最小的点作为我们估计出来的合理的椭球中心，即求取下式的最小值

求出椭球中心后，将坐标系的原点平移到椭球中心得到公式

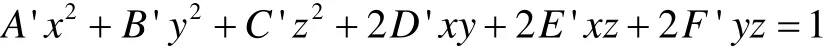
参照《空间解析几何》[6]中所述的方法，取6个点分别代入公式，求出椭球的3个半长轴的长度和偏角。

设对称矩阵S为

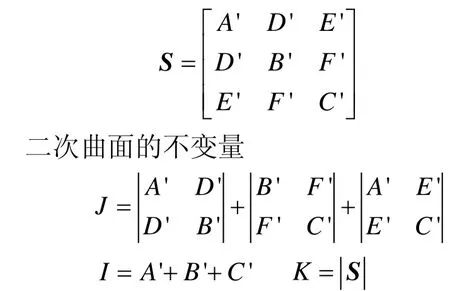
如果I, J, K都大于0，则证明所求系数代入上式中得到的二次曲面的确是椭球。设λ1,λ2,λ3为S的特征值，v1,v2,v3为对应的特征向量，那么 3个半轴的长度

2.3 椭球的验证

由于估计出来的椭球可能存在误差，在进一步地评估候选的好坏之前，先验证用于估计椭球的样本点本身是否能很好地符合估计出来的椭球，若估计时使用的所有样本点都能很好符合，则验证通过。为了验证，必须得到两个数据：样本点到椭球的距离d，样本点的法向与样本点在椭球面上的投影处的法向之间的偏角θ。当两个数据满足所给的阈值条件即d＜ε，θ＜α时，即认为此样本点可以很好符合椭球。

2.4 椭球的分数计算

椭球的分数就是点云中距离和法向偏角满足一定的阈值要求，且其投影点属于椭球的最大连通分量内的点的个数。直接在椭球面上求最大连通分量是困难的。因为计算椭球面上两点间沿椭球面的最短弧的长度是比较复杂的。在这里，为了简化，我们先将点都投影到一个平面的参数域上，通过计算平面参数域上的最大连通分量求得椭球面上的最大连通分量。

将椭球面上的点投影到参数平面之后，先要将参数平面位图化，然后在进行连通分量的检测。位图的像素的大小由原始数据的采样分辨率确定。如果一个像素的区域内存在椭球面上点的投影，那么这个像素将被着色。连通分量的计算过程是这样的，首先将每个像素的连通分量编号都设为-1，表示不属于任何分量。逐行扫描位图的每个像素，在扫描的过程中要记录每个已检测出的连通分量包含的像素点，如果扫描到的这个像素点未被着色，不做任何处理，如果这个像素着色了，则考察已经扫描过的与这个像素点相邻的像素点，将这些相邻像素点所属的连通分量合并，再加入当前的这个点得到一个新的连通分量，当扫描完毕之后就找到了所有的连通分量。包含像素点最多的就是最大连通分量。

3 实验结果及分析

本文算法在 VC＋＋平台上用 OPENGL实现。为了测试本文椭球提取算法的有效性，本文在人工合成和扫描仪获取的点云模型上展开了实验，并使用运行时间、拟合误差两个指标对算法的性能进行了定量描述。

首先，本文使用了一个手工创建的椭球模型并记录下其各个参数，并对此模型进行随机采样得到10万个点；然后运行本文算法，将得到椭球参数与真实参数进行比对。参数设置为：最大距离 ε = 0 .008*BB （BB为包围盒的对角线长度），最大偏角α=30°，最小形状的大小为τ=200，置信概率 pt= 9 9.9999%。图2中给出了球的检测结果，算法运行时间为1.1233秒，平均距离误差（指的是原始数据点到其在检测出的形状上的对应点的平均距离）为0.0003。表1则给出了原始椭球的数据与检测出来的椭球的数据的比较，结果表明，本文的方法能够正确地检测出椭球。

图2 人工合成的椭球的提取结果

表1 提取出的椭球参数与真实数据的比较

本文提出的算法应用到由激光扫描仪得到的原始点云模型，如图3所示。可以看到，在此点云模型中，每个人物的头部可以大致由椭球来进行拟合。我们为算法设置的参数为：最大距离ε= 0 .009*BB ，最大偏角α=40°，最小形状的大小为τ=200，置信概率 pt= 9 9.9999%。实验结果表明，在 RANSAC算法框架基础上，本文提出的算法能够在点云模型中检测并提取出来可以由椭球拟合的部分（例如人的头部），并得到很好的拟合结果。算法的运行时间为 58.5s，平均距离误差为0.0407，检测出51个基元。

4 结 论

基于RANSAC的形状检测已经能从点云中检测出平面，球，圆锥，圆柱，圆环等形状，为了能得到更为准确和复杂的基元表示，本文提出了一种在点云模型中提取椭球的算法。该算法使用了RANSAC框架；使用一种局部的采样策略进行采样；利用最小二乘的方法计算椭球的参数（中心点、半轴长和偏转角度）；利用距离和偏角进行椭球的初步验证，并通过一种低扭曲的参数化方法得到参数化平面计算出最大连通分量，完成了分数方程的计算，得到评估椭球的分数；最后依据分数筛选出最好的候选，通过求投影点的方法绘制出提取的椭球。在人工合成和扫描仪获取的点云数据上，本文验证了所提算法的有效性和鲁棒性。

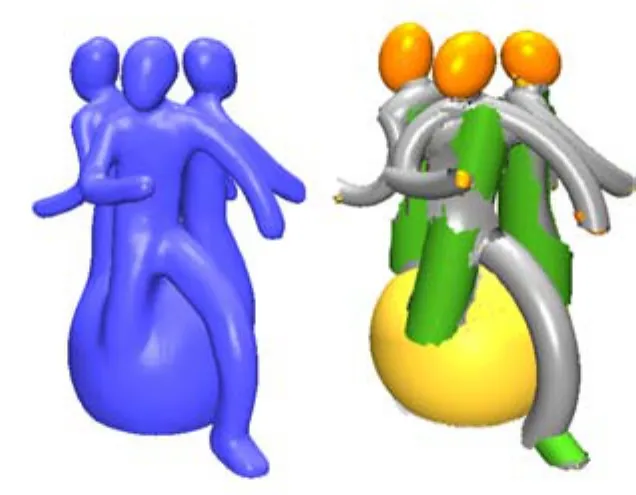
图3 真实扫描数据(上)的椭球(下)的提取结果

[1]刘金平, 程志全, 党 岗, 等. 三角网格中二次曲面的提取方法综述[C]//第 15届计算机辅助设计与图形学学术会议, 大连: 中国计算机学会, 2008: 134-139.

[2]Schnabel R, Wahl R, Klein R. Efficient RANSAC for point-cloud shape detection [J]. Computer Graphic Forum, 2007, 26(2): 214-226.

[3]Cohen S D, Alliez P, Desbrun M. Variational shape approximation [J]. ACM Transactions on Graphics,2004, 23(3): 905-914.

[4]Wu J, Kobbelt L. Structure recovery via hybrid variational surface approximation [J]. Computer Graphics Forum, 2005, 24(3): 277-284.

[5]Li B, Schnabel R, Jin S, et al. Variational surface approximation and model selection [J]. Computer Graphics Forum, 2009, 28(7): 1985-1994.

[6]杨文茂, 李全英. 空间解析几何[M]. 武汉: 武汉大学出版社, 1998: 128-135.