一道高考向量试题的解答及其推论

● 益民

(兰溪市第一中学 浙江兰溪 321100)

一道高考向量试题的解答及其推论

●李超李益民

(兰溪市第一中学 浙江兰溪 321100)

2012年浙江省数学高考文、理科的第15题都是对向量内容的考查，题目新颖，富有创意，简洁明了，源于教材又高于教材.本文主要给出3种不同解法，并对该题目进行扩展，得到一些推论.

本题的命题意图是考查学生对向量知识的理解应用能力，根据题目的条件，利用向量的一些法则来求解.

1 3种解法

解法1如图1所示，易知

cos∠AMB=-cos∠AMC，

根据余弦定理得

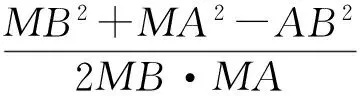
因为MB=MC，所以

AB2+AC2=2(AM2+BM2)=68,

又因为M为BC中点，所以

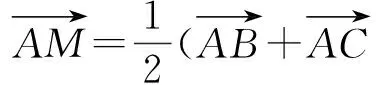
两边同时平方得

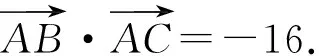
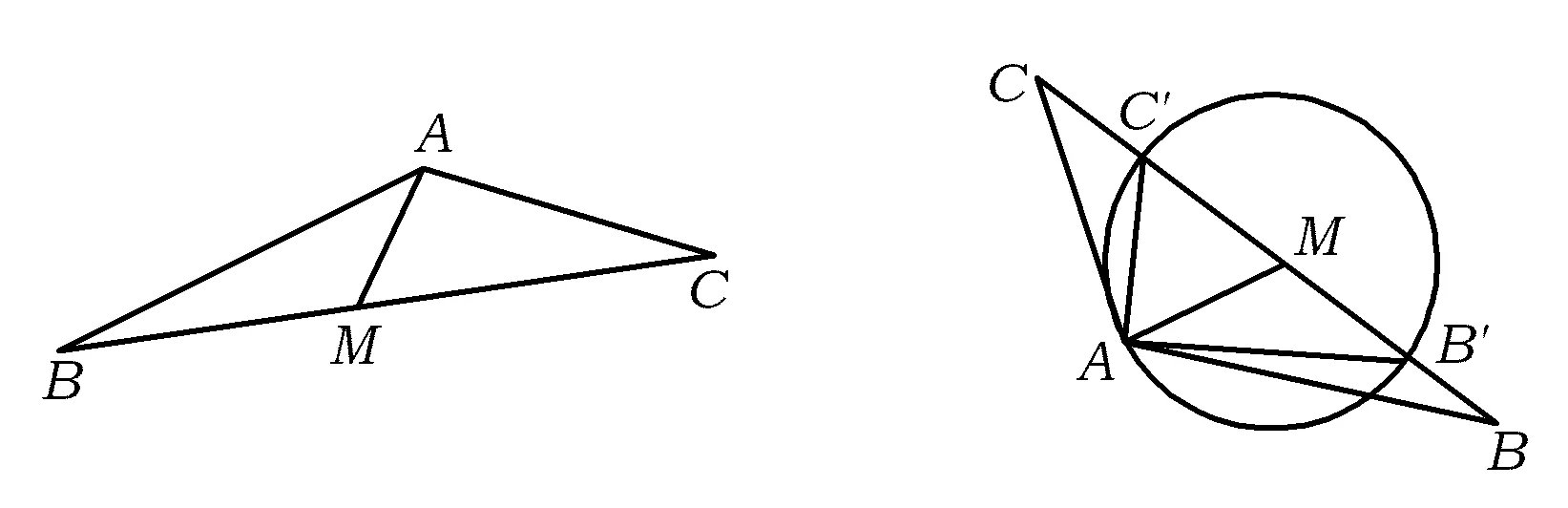
图1 图2

解法2如图2所示，以M为圆心，MA为半径作⊙M交边BC于点B′,C′，从而AB′⊥AC′，即

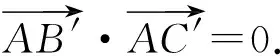
根据向量的三角形法则,知

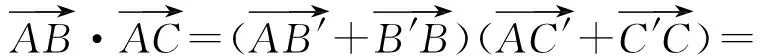
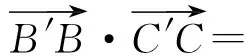
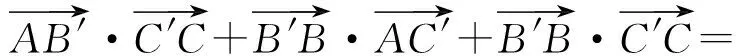
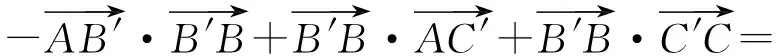
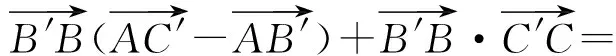
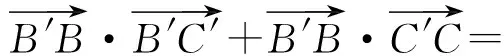
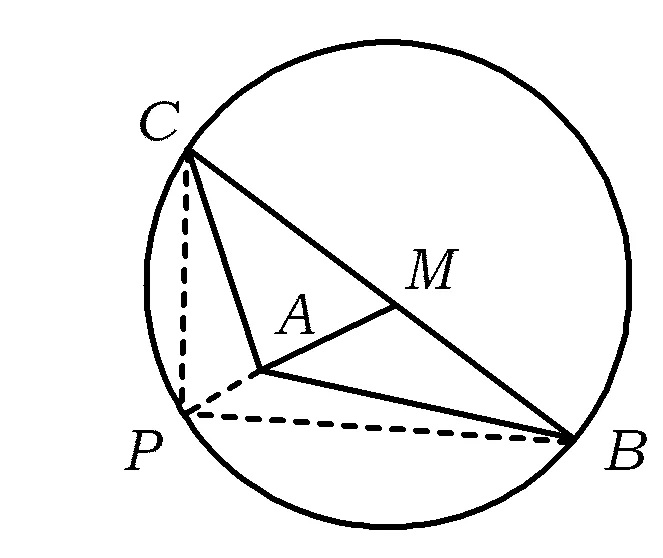
图3

解法3如图3所示，以M为圆心，BC为直径作⊙M，延长MA交⊙M于点P，从而PC⊥PB，即

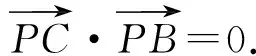
根据向量的三角形法则,知

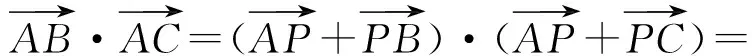
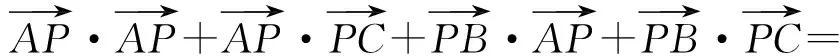
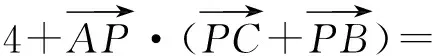
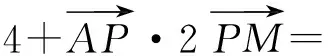
4-2×2×5=-16.

2 4个推论

证明如图4所示，当点P,A,B不共线时，点P,A,B可以构成一个三角形，PO为AB边上的中线.易知cos∠AOP=-cos∠BOP，根据余弦定理得

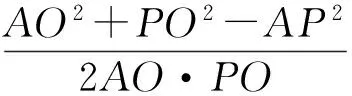
因为AO=BO，所以

AP2+BP2=2(PO2+AO2)=2(r2+a2),

又因为O为AB中点，所以

两边同时平方得

当点P,A，B共线时，

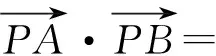
-(r-a)(r+a)=a2-r2(定值).

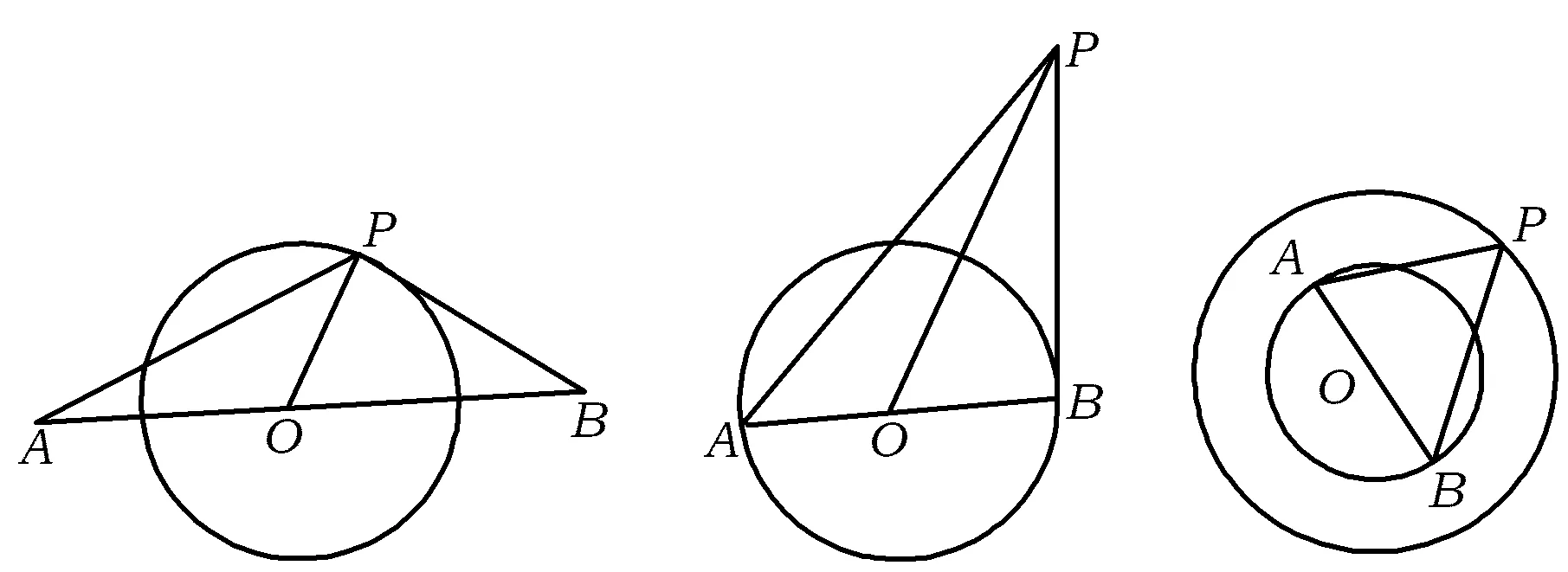
图4 图5 图6

证明如图5所示，方法同推论1.

证明如图6所示，方法同推论1.

AM2=λAC2+μAB2-λμBC2,

其中λ+μ=1.

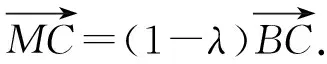
由余弦定理,知

同理

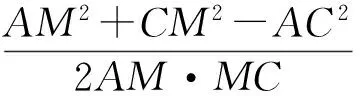
又因为cos∠AMB=-cos∠AMC，所以

将BM=λBC,MC=(1-λ)BC代入上式整理得

从而(1-λ)AM2+(1-λ)λ2BC2-

(1-λ)AB2+λAM2+λ(1-λ)2BC2-λAC2=0,

整理得

AM2=λAC2+(1-λ)AB2-λ(1-λ)BC2.

令μ=1-λ，则

AM2=λAC2+μAB2-λμBC2.