求解指标1的微分代数方程组的一类新方法

鲍文娣, 韩海力

(1.中国石油大学 理学院, 山东 青岛 266552； 2.青岛杰瑞自动化有限化司, 山东 青岛 266071)

求解指标1的微分代数方程组的一类新方法

鲍文娣1, 韩海力2

(1.中国石油大学 理学院, 山东 青岛 266552； 2.青岛杰瑞自动化有限化司, 山东 青岛 266071)

给出求解指标1的微分代数方程组的一类新的计算方法．将微磁学仿真的方法推广到求解微分代数方程组,并给出方法的收敛性和相容性分析． 利用与伴随法相复合的方法,提高方法的收敛阶．并将方法应用于晶体管放大器的模型中．数值实验表明方法是有效的．

Gauss-Seidel方法; 微分代数方程组; 伴随法; 投影法

0 引言

许多重要的数学模型都表示为微分代数方程组的形式, 它在各式各样的科学工程都有应用．例如:大规模电路分析、计算机辅助设计、多体动力系统的实时仿真、能源系统、化学反应仿真、最优控制等等．很多物理中的问题最初的模型即为一个微分代数方程组的形式．

近些年来,微分代数方程组的求解已成为近十年来研究的热点问题．一些求解微分代数方程组的数值方法得到了进一步的发展,如Padé逼近、波行迭代法[2-10]等.

本文提出一类新的数值方法,探讨应用复合的Gauss-Seidel法和SOR方法来求解微分代数方程组,并进一步给出方法的收敛性分析．在第2部分构造适用于微分代数方程组的复合Gauss-Seidel法和SOR方法,并给出了方法的误差估计．在第三节中,就用于求解晶体管放大器模型和摆模型中．最后,在第四节中给出结论.

1 求解微分代数方程的数值方法

1.1 非线性微分代数方程组

考虑下面的微分代数方程组:

(1)

其中x∈Rnx,y∈Rny,f∈Rnx,g∈Rny,并且设(1)中的微分代数方程组指标为1,也就是说g(x(t),y(t))关于y的Jacobian矩阵gy在(1)的解的邻域内是可逆的．

众所周知,一般的前Euler方法(2)求解微分代数方程组时,是不稳定的．下面我们用考虑Gauss-Seidel方法来修正(2)式．

1) 前Euler方法:

(2)

2) 显式的Gauss-Seidel方法:

(3)

3) 隐式的Gauss-Seidel方法:

(4)

4) SOR方法

(5)

通过比较发现上述四种方法中,隐式的方法最稳定．为了提高误差阶,将复合法来求解指标1的微分代数方程组．利用Taylor展开式,可得

yn-y(tn)=O(h),xn-x(tn)=O(h),

yn-y(tn)=O(h2),xn-x(tn)=O(h2)．

若Jacobian矩阵gy满足Lipschitz条件‖gy(x,φ(x))‖≤L,则由文[10]中的定理3.4可知全局误差E=x(t)-xN满足:

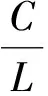
(6)

其中t0为初始时间,xN是第N步的数值解,C是独立于h的常数．(6)式说明复合法是一阶精度的全局收敛的方法．

1.2 线性微分代数方程组

考虑下面的微分代数方程组

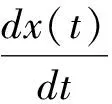
(7)

矩阵B(t)分裂成B(t)=D(t)-L(t)-U(t),其中D(t)是对角元素,L(t)和U(t)分别为下三角和上三角矩阵．利用Euler方法,(7)式可写成下面的形式:

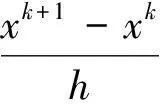
由SOR迭代,有

(h(D-wL)+wA)x(k+1)=(h(wU+(1-w)D)+wA)xk+whf

(8)

其中w为参数．若h(D-wL)+wA可逆,则问题有唯一的数值解x(k+1),并且只有当(wA,D(t)-wL(t))是正则时才有可能．所以为了方法能正常使用,需要假设矩阵对(wA,D(t)-wL(t))对于所有的t∈I是正则的．

注1 1) 当w=1时,(8)为Gauss-Seidel法;2) 方法(7)的误差估计和稳定性可由Taylor展开得到,经计算局部误差为O(h2)；3) 对于大规模方程组方法(8)简单有效．

2 数值实例

例1 晶体管放大器(图1),图中Ue(t)为输入电压,Ub(t)为工作电压,Ui(t)(i=1,2,3,4,5)分别为节点1,2,3,4,5处的电压,U5(t)为输出电压．电流通过电阻时满足I=U/R, 电流通过电容时有I=C·dU/dt,其中R,C为常数,U为电压．晶体管是这样工作的,将来自节点3、4 的电流放大到节点2到节点3的电流的99倍,这依赖于电压差U3-U2．Kirchhoff表述为在任一时刻汇集于电路中任一节点的各支路电流的代数和等于零．将这一法则应用于图1中的节点5可得下面的方程组:

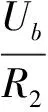
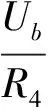
(9)

初始信号为:Ue=0.4sin(200πt)．由稳式的Gauss-Seidel 法复合而得到的复合法应用到晶体放大器问题(9)中,其数值解由图2给出,比较输入Ue和输出电压U5(t)可知我们的方法是有效的．

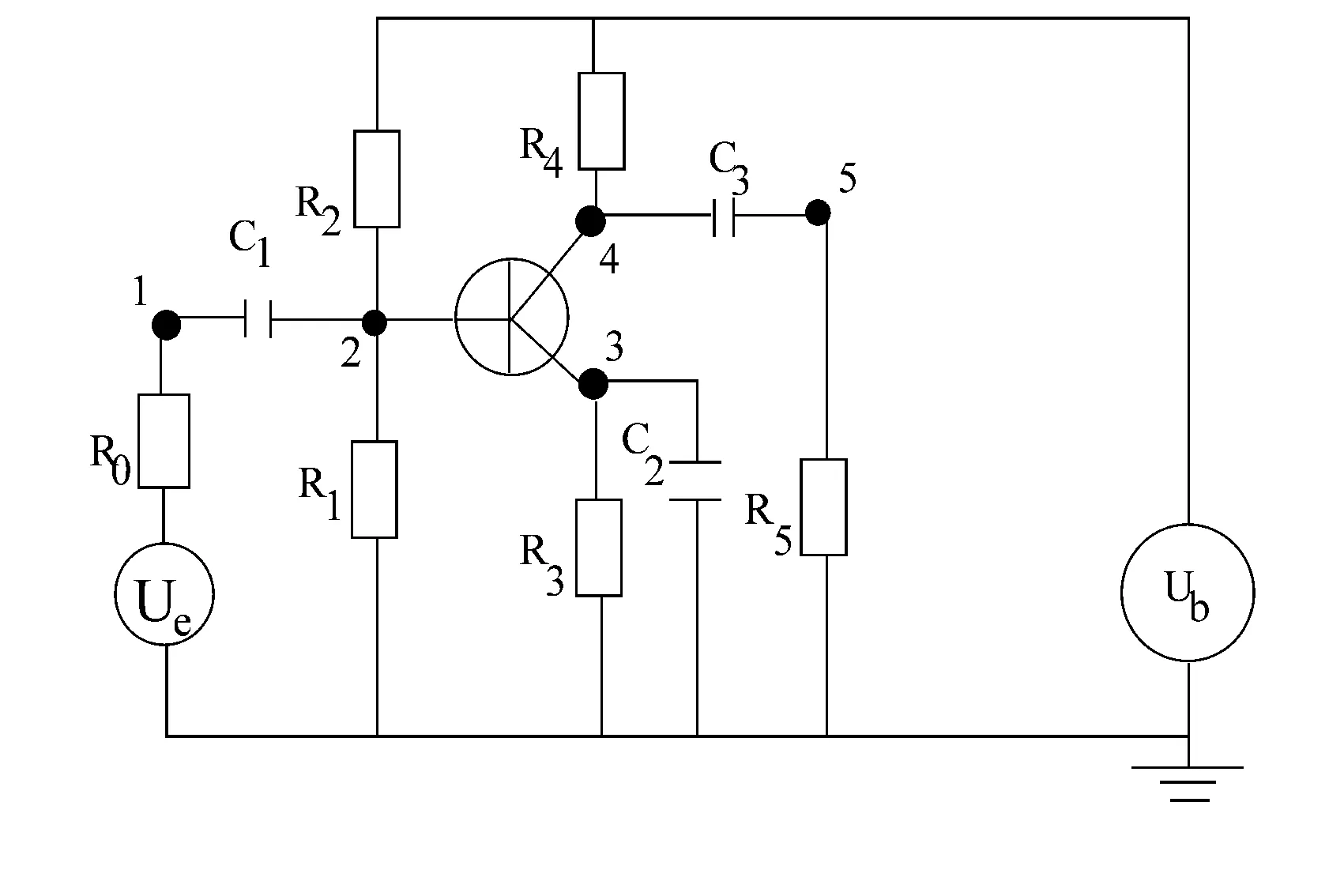
图1 晶体管放大器原理图

例2 图2中(摆)悬挂在可忽略质量的长为l的棒上的质点m,在重力g作用下进行摆动．设质点所在位置坐标为(p,q),则运动满足下面的方程:

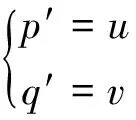
(10)

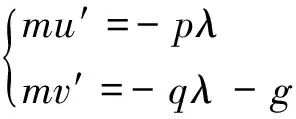
(11)

0=p2+q2-l2

(12)

其中(u,v)是速度,λ是棒的张力．表达式(6)是指标为3的微分代数方程组．微分一次可得:

0=pu+qv

(13)

从几何上理解为速度为流形(13)的切线,也就是说正交于梯度2(p,q)．方程组(10) (11) (13)是指标为2的形式．再微分一次并且由(12)可得:

0=m(u2+v2)-gq-l2λ

(14)

则方程组(10) (11) (14)为指标1的形式．将显式的Gauss-Seidel 方法应用于带有下面相容初始条件的微分代数方程组(10) (11) (14)中,

p(0)=1,q(0)=0,u(0)=0,v(0)=0,λ(0)=0,

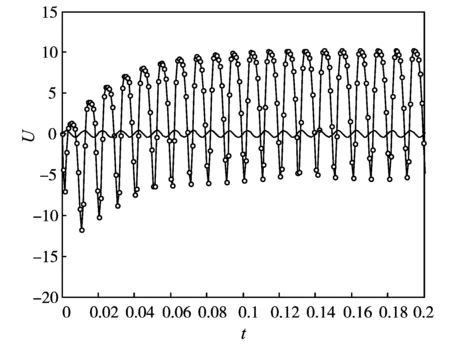
图2 输入电压Ue与输出电压U5(t)关系

则有下列关系式:

(15)

(16)

(17)

显然公式(15)-(17)是精度为1阶的复合法(文[11]中的可分的Runge-Kutta法,当s=1时)．由图3和图4可以看出我们的复合法能得到与文[12]中RADAU5类似的结果．

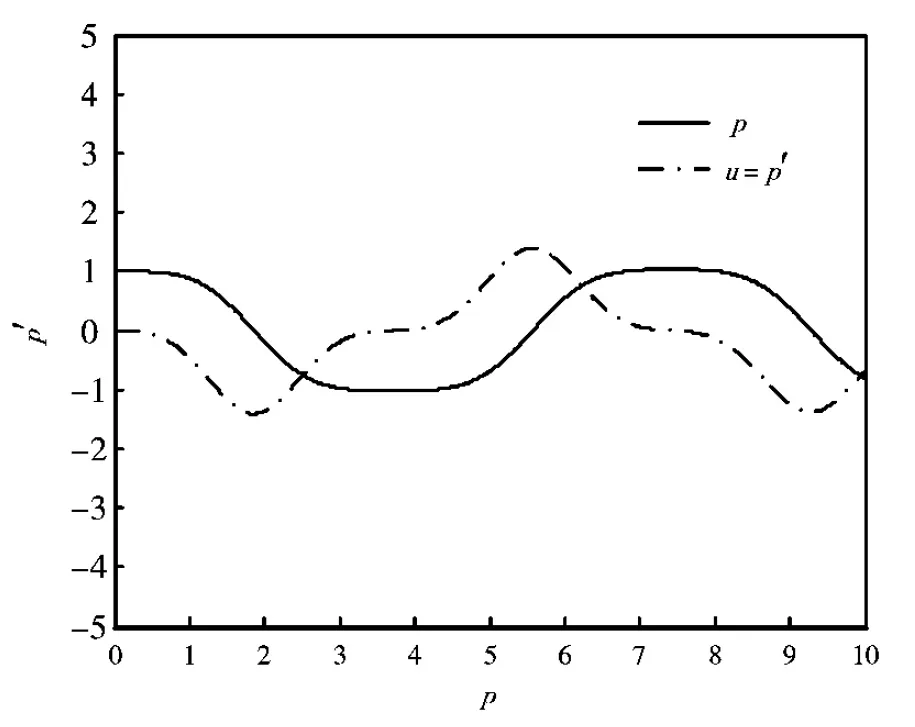
图3 p和它的导数p′的数值解

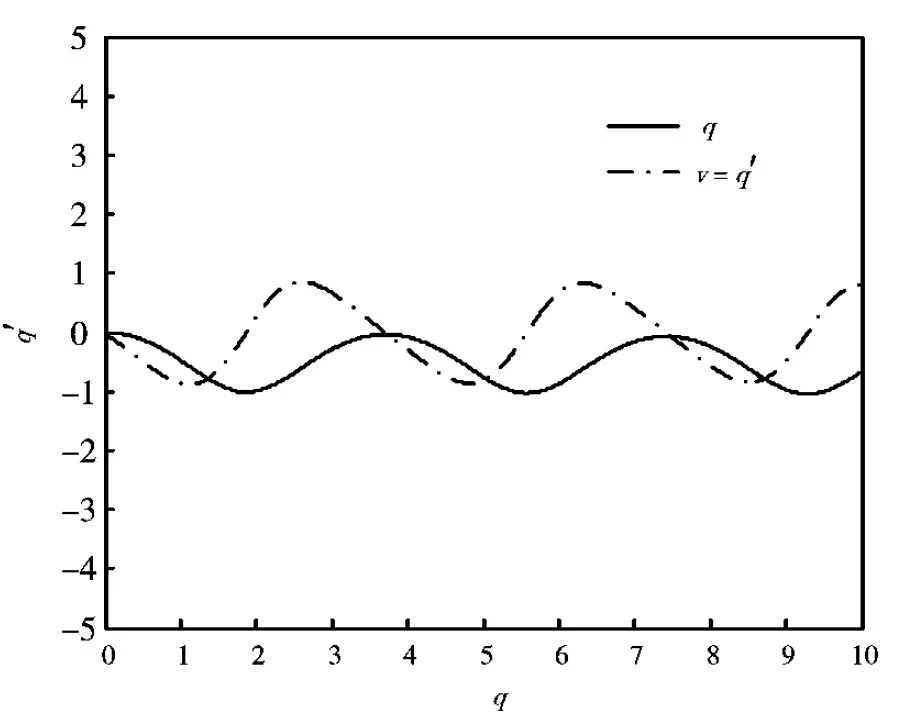
图4 q和它的导数q′的数值解

3 结论和展望

文中给出了求解微分代数方程的Gauss-Seidel 方法和 SOR方法．将复合的Gauss-Seidel方法应用到晶体管放大器的模型中,结果表明方法是有效的．另一方面,将Gauss-Seidel法与投影法相复合用于求解摆振动问题．两种方法简单易实现,所以适用于工程计算中．然而,方法的精度较低,且只用于求解指标1的微分代数方程组．考虑高精度的适用于高指标的微分代数方程组的计算方法是我们下一步的工作．

[1] Wang X P, Carlos J. Garcia-Cerververa, Weina E. A Gauss-Seidel Projection method for miscromagnetics simulations[J]. Journal of computational physics, 2001, 171:357-372.

[2] Jiang Y, Wing O. Convergence conditions of waveform relaxation methods for circuit simulation[J]. Proceedings of the 1998 IEEE International Symposium on Circuits and Systems, 1998, 6: 232-235.

[3] Leimkuhler B, Miekkala U, Nevanlinna O. Waveform relaxation for linear RC-circuits[J], IMPACT of Computing in Science and Engineering. 1991, 3: 123-145.

[4] Miekkala U. Dynamic iteration methods applied to linear DAE systems[J]. J Comput. Appl.Math. 1989, 25: 133-151.

[5] Song Y. Waveform relaxation methods and accuracy increase[J]. Ann of Diff Eqs, 1995,11: 440-454.

[6] Roberto Barrio. Performance of the Taylor series method for ODEs/DAEs[J]. Applied Mathematics and Computation, 2005,163: 525-545.

[7] Wang H S. Numerical solutions of Hamiltonian DAEs and applications[J]. Applied Mathematics and Computation, 2006, 180: 97-110.

[8] Brenan K E, Campbell S L, Petzold L R. Numerical Solution of Initial Value Problems in Differential Algebraic Equations[M]. Elsevier, New York, 1989.

[9] Hairer E, Norsett S P, Wanner G.Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems[M]. Springer, New York, 1992.

[10] Hairer E, Norsett S P, Wanner G. Solving Ordinary Differential Equations I. Stiff and Differential-Algebraic Problems[M]. Springer, New York, 1992.

[责任编辑：李春红]

ANewClassofMethodsforDifferential-algebraicEquationsofIndex-one

BAO Wen-di1, HAN Hai-li2

(1.School of science, China University of Petroleum, Qingdao Shandong 266552, China)(2.Qingdao JARI Automation Co., Qingdao Shandong 266071, China)

In this paper, a new class of methods for solving the index-1 differential-algebraic equations are proposed. The methods are the extensions of gauss-seidel method to DAEs. In order to increase the convergence order, the composition with the adjoint method is provided and then the convergence of the composition method is given. The numerical tests applied to problems from an amplifier and a pendulum show the algorithms are feasible.

gauss-seidel method; differential-algebraic equations (DAEs); adjoint method; projection method

O175.22

A

1671-6876(2012)02-0117-05

2012-02-16

鲍文娣(1979-), 女, 河北武邑人, 讲师, 博士研究生, 研究方向为矩阵计算及微分代数方程组求解.