Structure theorem for Hopf group-coalgebra

Dong Lihong Wang Shengxiang Wang Shuanhong

(1Department of Mathematics, Southeast University, Nanjing 211189, China)(2College of Mathematics and Information Science, Henan Normal University, Xinxiang 453007, China)

As a generalization of a Hopf algebra, Turaev[3]introduced and studied the notions of Hopfπ-coalgebras. Further study is referred to Virelizier[4]and Wang[5-7]. It is now very natural to ask whether we can extend the main result in Ref.[2] to the setting of Hopfπ-coalgebras. This is the motivation of this paper.

1 Preliminaries

In this section we recall some basic definitions and results about Hopfπ-coalgebras introduced by Turaev[3]. Throughout this paper, letkbe a field. The reader is referred to Sweedler[8]about Hopf algebras.

1.1 Semi-Hopf π-coalgebra

Recall from Turaev[3]that aπ-coalgebra is a family ofk-spacesC={Cα}α∈πtogether with a family ofk-linear mapsΔ={Δα,β:Cαβ→Cα⊗Cβ}α,β∈πand ak-linear mapε:C1→k, such thatΔis coassociative in the sense that,

(Δα,β⊗idCγ)Δαβ,γ=(idCα⊗Δβ,γ)Δα,βγ∀α,β,γ∈π

(idCα⊗ε)Δα,1=idCα=(ε⊗idCα)Δ1,α∀α∈π

A semi-Hopfπ-coalgebra is aπ-coalgebraH=({Hα},Δ,ε) such that eachHαis an algebra with multiplicationmαand unit element 1α∈Hα; and for allα,β∈π,Δα,βandε:H1→kare algebra maps.

1.2 Right π-H-comodule algebra

1.3 Relative Hopf π-comodule

LetHbe a semi-Hopfπ-coalgebra andAa rightπ-H-comodule algebra. If thek-spaceMis a rightπ-H-comodulelike object, andMis a leftA-module such that, for anya∈A,m∈M,

thenMis called a left-right relative (A,H)-Hopfπ-comodule.

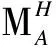
2 Structure Theorem of Endomorphism Algebras of Two-Sided Relative (A,H)-Hopfπ-Comodule

In this section, we always assume thatHis a semi-Hopfπ-coalgebra and each componentHαis projective, andAis a rightπ-H-comodule algebra.

Definition1Thek-vector spaceMis called a two-sided relative (A,H)-Hopfπ-comodule if 1)Mis a leftπ-H-and rightAbimodule; 2)Mis a right relative (A,H)-Hopfπ-comodule; and 3)Mis a left-right Hopfπ-H-comodule.

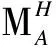
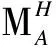
g→(h⊗m)=gh⊗m,(h⊗m)←a=h⊗m·a

∀g,h∈Hα;a∈A;m∈M

ρ(h⊗m)=h(1,a)⊗m[0,0]⊗h(2,β)m(1,β)

∀h∈Hαβ,m∈M

In particular,H⊗A={Hα⊗A}α∈πis a two-sided relative (A,H)-Hopfπ-comodule.

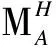
ρβ(f)(m)=f(m[0,0])[0,0]⊗f(m[0,0])[1,β]Sβ-1(m[1,β-1])

(1)

for anyf∈HomA(M,N),m∈M, whereN⊗Hβis a rightA-module via (n⊗h) ·a=n·a⊗hfor anyn∈N,h∈Hβ,a∈A. Then, it is easy to see thatρβ(f) is a rightA-module map.

ArightA-linearf:M→Nis called rational if there exists an elementf[0,0]⊗f[1,β]∈HomA(M,N)⊗Hβsuch that

f[0,0](m)⊗f[1,β]=f(m[0,0])[0,0]⊗f(m[0,0])[1,β]Sβ-1(m[1,β-1])

(2)

for anym∈M. Define

HomA(M,N)={f∈HomA(M,N)|fis rational}

Since eachHβis projective, HomA(M,N) may be viewed as a submodule of HomA(M,N⊗Hβ). And by Eqs.(1) and (2), for anyf∈HomA(M,N), we know that

ρβ(f)=f[0,0]⊗f[1,β]

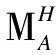
ρβ(f)=f[0,0](m[0,0])⊗f[1,β]m[1,β]

for anym∈Mandf∈HomA(M,N).

As described above, we can easily obtain the following lemmas.

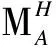
1)ρ(f)={ρβ(f)∈HomA(M,N)|⊗Hβ}β∈πfor anyf∈HomA(M,N), and HomA(M,N) is a rightπ-H-comodulelike object;

2) ENDA(M,N) is a rightπ-H-comodule algebra;

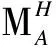
(h→f)(m)=h(1,α)·f(Sα-1(h(2,α-1)) ·m)

(3)

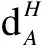
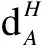
Now we can obtain the main result of this paper.

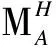
1) There exists an isomorphism of right relative (A,H)-Hopfπ-comodules,

N≅HOMA(A,N)

where HOMA(A,N) is a rightA-module viaf·a(b)=f(ab).

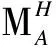
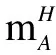
is an isomorphism of right Hopfπ-H-comodules, whereg∈HOMA(A,N) andh∈Hα. Furthermore,

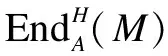
is an isomorphism of right Hopfπ-Hcomodules and algebras.

ProofWe have a well-defined map

φ:N→HOMA(A,N)φ(n)(a)=n·a

sinceρβ(φ(n))(a)=φ(n[0,0])(a)⊗n[1,β]for anyn∈Nanda∈A. It is easy to show thatφ:HOMA(A,N)→N,f|→f(1A) is the inverse ofφ.

In a similar way to Lemma 2, we know that HOMA(A,N) is a right relative (A,H)-Hopfπ-comodule. It is easy to prove thatφis a right relative (A,H)-Hopfπ-comodule map.

The conclusion follows from Theorem 2.7 in Ref.[4] and 3) of Lemma 1, Lemma 2 and Lemma 3, which completes our proof.

By Theorem 1, we have the following remark.

Remark1) By 1) of Theorem 1,A≅ENDA(A), which is an isomorphism of rightπ-H-comodule algebras. In particular,H≅ENDH(H), which is an isomorphism of algebras.

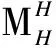
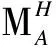
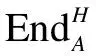
[1]Doi Y. On the structure of relative Hopf module[J].CommAlgebra, 1983,11(3): 243-255.

[2]Ulbrich L H. Smash products and comodules of linear maps[J].TsukubaJMath, 1990,14(2): 371-378.

[3]Turaev V.Homotopyquantumfieldtheory[M]. Zürich, Switzerland: European Mathematical Society, 2010.

[4]Virelizier A. Hopf group-coalgebras[J].JPureApplAlgebra, 2002,171: 75-122.

[5]Wang S H. Group twisted smash products and Doi-Hopf modules forT-coalgebras[J].CommAlgebra, 2004,32(9): 3417-3436.

[6]Wang S H. Group entwining structures and group coalgebra Galois extensions[J].CommAlgebra, 2004,32(9): 3437-3457.

[7]Wang S H. Morita contexts,π-Galois extensions for Hopfπ-coalgebras[J].CommAlgebra, 2006,34(2): 521-546.

[8]Sweedler M.Hopfalgebras[M]. New York: Benjamin, 1969.