用等效法求简谐运动的周期

曹聪明 武维

(包头市第九中学 内蒙古 包头 014010)

简谐运动典型模型有单摆和弹簧振子，在很多问题中出现了并非纯粹的单摆或弹簧振子模型，因此就不能直接使用公式

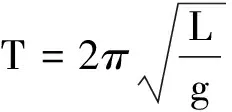
求解运动周期．从单摆的周期公式中可以看出，与周期有关的参量分别是单摆的摆长L和重力场强g；从弹簧振子周期公式可以看出，与周期有关的参量分别是振子的质量m和劲度系数κ．因此，对于一些并非纯粹的单摆或弹簧振子模型，我们可以从这些方面发现它们的等效性，使之转化为可直接用单摆周期公式或弹簧振子周期公式求解的等效模型而求出它们的周期．

1 等效摆长

【例1】如图1所示，一质量为M的车厢静止在光滑水平面上，厢顶悬一摆长为L,摆球质量为m的单摆，单摆摆动时此摆的周期为多少？

图1

解析：由于车和球的系统不受合外力，故系统质心在地面参考系中是定点．我们知道，单摆的运动是以其自然状态下的竖直位置为对称中心的，即单摆的运动坐标为x=Lsinθ．在本例中，摆球必定以系统质心所在竖直位置为对称中心，质心在水平方向上与小球相距

因而其等效摆长为

由分析可知，车厢中的单摆做简谐运动的等效摆长为

因此振动系统的周期为

图2

解析：用C球替代人，它实际上是在绕AB轴摆动，根据摆动的物理情景可知，小球的悬点可以看成是AB线上的任意一点．

思路一：若选E为悬点，类似将单摆放置在光滑斜面上的情形，故等效重力加速度

所以

思路二：若选D为悬点，不需要分解重力加速度，等效摆长L=CD，过C点做AB的垂线交点为E，有

解得

所以

【例3】一个单摆，由一根长为l的刚性轻杆和两个质量均为m的小球组成，一个小球固定在轻杆末端，另一个小球固定在轻杆中央，求这个(单)摆的周期．

解析：此时的摆动模型实际为复摆，高中阶段并不研究、不学习复摆的周期，所以只能采用等效代替的思想完成此问题．

设此(单)摆偏离平衡位置的角度为θ，从静止释放到达到平衡位置的角速度为ω,根据机械能守恒定律有

解得

设有一个摆长l′的单摆与此(单)摆等效，摆长为l′的单摆偏离平衡位置角度为θ，从静止释放，到达平衡位置的角速度为ω′，根据机械能守恒定律有

解出

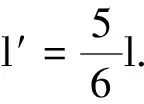
2 等效重力加速度

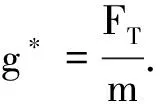
【例4】如图3所示，一辆小车以加速度a做匀加速直线运动，车内有一单摆，摆长为L，小球质量为m,求这个单摆的摆动周期．

图3

解析：小球相对小车做摆动，它相对小车做摆动的平衡位置不在竖直位置，设它在A位置，以车为参考系(非惯性参考系)，小球受力如图4所示．

图4

根据题意可列出方程

mgsinα=macosα

mgcosα+masinα=T

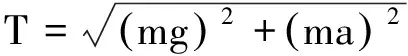
则等效加速度

3 等效质量

根据牛顿第二定律列出方程与振动标准方程比较，求等效质量．

【例5】如图5所示，劲度系数为κ的轻弹簧竖直悬挂，下端与质量为M的圆柱体(不能转动)连接，不能伸长的细线绕过圆柱体，两端分别系有质量为m1和m2的重物，细绳与圆柱体的摩擦可忽略不计，试求两重物同时运动时，圆柱体的振动周期．

图5

解析：设两重物同时运动时，M的加速度为a，方向向下，以M为参照物(为非惯性系)．以m1和m2为研究对象，根据牛顿第二定律有

m1g-m1a+m2a-m2g=(>m1+m2)a相对

(1)

以m1为研究对象以地面为参考系，根据牛顿第二定律有

m1g-T=m1(>a相对+a)

(2)

再以M为研究对象以地面为参考系，根据牛顿第二定律有

2T+Mg-κx=Ma

(3)

由式(1)有

代入式(2)有

代入式(3)有

设

则

可知等效质量

因此周期

【例6】如图6所示，已知m1,m2，κ．滑轮质量不计，滑轮与轮轴及细线间摩擦不计．求：系统振动的周期．

图6

解析：m1和m2的振动周期相同，由振动的过程可知m1和m2位移关系:s2=2s1.进一步可知m1和m2加速度关系为

a2=2a1

由牛顿第二定律可知

2T-m1g=m1a1

κx+m2g-T=m2a2

整理

进一步整理可得

设

则有

类比可知等效质量

所以周期

4 等效比例系数

根据受力情况分析回复力，写出回复力的表达式与标准方程比较，求出等效比例系数．

【例7】如图7所示,振动系统κ1=κ2=κ，如果不计两滑轮的质量及一切摩擦，则该系统在竖直方向上振动的周期是多少.

图7

解析：设弹簧又伸长Δx，以m为研究对象，m离开平衡位置的位移为4Δx，由于滑轮质量不计，细绳中张力为

则物体受到的回复力为

对m进行研究列出标准方程，可知F回=κ等效Δxm，又因为Δxm=4Δx，则F回=4κ等效Δx，即

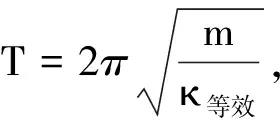
【例8】如图8所示，轻杆一端铰链另一端用劲度系数为κ1的弹簧拉着．B点悬挂一个弹簧振子，整个系统处于平衡状态，已知a,b,κ1,κ2,m．求这个振动系统的周期.

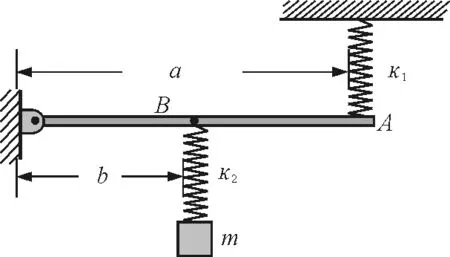
图8

解析：用力向下拉m，使弹簧κ2又伸长Δx2，释放m．整个系统开始振动．以m为研究对象．它受到的回复力设为F，有

F=κ2Δx2=κ等效Δx

Δx=Δx2+ΔxB

由轻杆力矩平衡可知

κ1Δx1a=κ2Δx2b

根据三角形相似可知

其中Δx是物体偏离平衡位置的位移，ΔxB是B点向下移动距离， Δx1是弹簧κ1在原基础上的伸长量．

整理可知

进一步整理可知

解得

所以

通过这部分知识的学习，增强了学生学习物理的兴趣，提升解决物理问题思维和方法． 高中物理特别注重物理方法的理解和掌握，因此我们在竞赛辅导过程中有意识的借助一定的物理情景，让学生体会如何构建物理模型，如何通过与标准形式进行比较，找到合理等效量，在解决问题中体会等效法的美妙之处，进而掌握等效法．

参考文献

1 罗金明．等效法确定单摆周期公式中的“l”和“g” ．数理化学习(高中版)，2004(3)

2 陈丽欣．等效思想的充分应用单摆周期公式的分析与比较．物理通报，2010(7)

3 金凤官．单摆周期公式的理解与灵活应用．物理教学探讨，2009(33)

4 陈洪武．从机械能守恒的角度推导单摆简谐振动的周期．物理与工程，2012，22(1)

5 沈晨．更高更妙的物理．杭州：浙江大学出版社，2006

6 王国德. 高考-奥赛全程对接-高中物理2-5版.北京：机械工业出版社，2008