媒质中电磁波传播的FDTD仿真
周珩
南京工程学院通信工程学院,江苏 南京 211167
1 概述
FDTD算法是1966年K.S.Yee在一篇论文里提出的,直接将带时间变量的麦克斯韦方程转化为差分形式来求解空间电磁场的算法。它是把电磁场的电场和磁场分量分别在时域和空域上进行差分,利用蛙跳式算法在时间和空间内进行交替抽样计算,通过时间轴上更新来模仿电磁场的变化,达到数值计算的目的。
随着计算技术特别是电子计算机技术的飞速发展,FDTD法得到长足发展,在电磁学、电子学和光学等领域都有非常广泛的应用,包括天线设计,微波电路设计,电磁兼容分析,电磁散射计算,光学应用等等。本文就是基于FDTD方法对电磁波在不同媒质中传播的反射特性进行模拟的。
2 应用FDTD法的关键技术
为应用FDTD法解决电磁波传播所遇到的实际问题,有以下几个方面的关键技术,包括计算区域的适当网格剖分、电磁波源的设置及理想匹配层的设置等。这几个方面的问题分述如下:
1)计算区域的适当网格剖分
将Maxwell旋度方程在直角坐标系下的六个分量方程


在图1所示Yee网格中进行有限的差分离散化,在某些参数或场分量为零的情况下,有限差分式可以进一步简化成二维甚至一维的形式。任意离散的时空点处的场分量F(F为磁场H或电场E)可以简记为
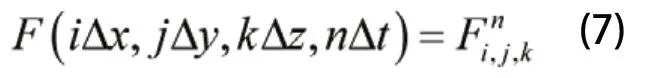

图1 Yee空间网格单元
2)源的设置
在FDTD中对源的设置方法有多种。但当目标远离入射场时,入射场可看成是平面波,因此计算中需要对平面波源加以设置。设置平面波源的关键是将计算主区域划分成总场区与散射场区,并且在总场区与散射场区的分界处加入入射的平面波。对于一维情况,一般可以采用点源。
3)理想匹配层(PML)的设置
为了解决使用FDTD法进行电磁计算时有限的计算资源的限制,可通过使用PML截断电磁场实际存在的无限区域来解决。目前广为采用的一种PML是各向异性理想匹配层(UPML)。假设计算区域中三个方向的电导率分别为σx、σy及σz,相对介电常数和相对磁导率仍为ε和μ,则UPML中的相对介电常数和相对磁导率分别为εs和μs,其中s为

这样,主计算区域与UPML区域就可以统一处理,但是对于不同区域,参数取值不同。例如:对于主区域,参数取值为sx= sy= sz=1;对于x向PML区域,参数取值为sy= sz=1;对于x向与y向PML相交区域,参数取值为sz=1;对于三个方向的PML相交区域,则sx、sy与sz均不为1。
如前所述,PML也可看成是一种特殊的媒质,它的电导率σ不是一个常数,而是一个空间变量的函数。各个方向的σ为

其中

式(11)中m通常取3~4;而R(0)对于5单元厚的PML层取e-8较好,对于10单元厚的PML层取e-16较好。
由于σw为函数,则各网格中的σw可取为PML层中某一段的平均值,即
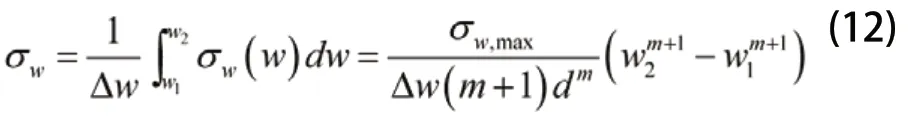
3 应用FDTD对电磁波在媒质中传播实例的仿真
由于用于隐身的涂层材料必须能够吸收入射的电磁波,因此这种材料必然是有损耗的,即相对介电常数不再只是一个常实数,而一个复数,甚至是频率的函数。我们以所谓的Debye材料为例,其相对介电常数为

现取εr=2,σ=0.01,χ=2及τ0=1e-9,而第一层媒质仍为自由空间。在FDTD算法中,设入射波为一高斯脉冲,总网格点数为200,两层媒质的分界面在网格点ndiv=100处,图2(a)为脉冲处于第一层媒质中,图2(b)为脉冲已进入第二层媒质,图2(c)为脉冲在第二层媒质中持续前进,对比图2(b)与(c)可见,波已发生明显衰减。图3为f=500MHz时的空间各点场强归一化分布,由该图也可看出波在第二层媒质中是不断衰减的,而在第一层中是不衰减的,因此呈现出明显的驻波形式,可求得其反射系数为0.2374。

图2 电磁波在两层媒质中的传播

图3 f=500MHz时的空间各点场强归一化分布
4 结语
在这篇文章中我们以FDTD方法仿真了电磁波在媒质中传播时,场在各媒质中的分布情况。结果表明,FDTD法能够模拟波的自然传播情况,并能显示全空间的场强分布,在电磁波的传播分析中有着巨大优势。
[1]Allen Taflove, Susan C. Hagness. Computational Electrodynamics: The Finite-Difference Time-Domain Method. Boston, London: Artech House. 2000
[2]Kai Chang. Encyclopedia of RF and microwave engineering[M]. New Jersey :Wiley & Sons, Inc., 2005.

