二元域上三次和四次剩余码的幂等生成元

1.大连大学 信息工程学院，辽宁 大连 116622

2.赤峰学院 附属中学，内蒙古 赤峰 024000

3.辽宁师范大学 数学学院，辽宁 大连 116029

1.大连大学 信息工程学院，辽宁 大连 116622

2.赤峰学院 附属中学，内蒙古 赤峰 024000

3.辽宁师范大学 数学学院，辽宁 大连 116029

1 引言

在通信系统中，为提高信息传输可靠性，广泛使用了具有一定纠错能力的信道编码技术，如奇偶校验码、汉明码、循环码等编码技术。二次剩余码是特殊的循环码，又是汉明码和格雷码的推广。因此研究二次剩余码以及它们的推广形式具有重要的理论意义和实际价值。文献[1]的第十六章讨论了二元域F2上四种二次剩余码之间的关系，给出了四种二次剩余码的幂等生成元。文献[2]用幂等生成元定义了有限环Z4上的二次剩余码。文献[3]证明了在有限环Z2k上由幂等元定义的二次剩余码存在，且只有4个。另一方面，文献[4-7]定义了有限域Fq上的高次剩余码，给出了这些码生成多项式的形式。高次剩余码的生成多项式都是多项式xn-1的因式。然而要求出这些高次剩余码，就需要在有限域Fq上分解 xn-1。当n很大时，这是一件十分困难的任务。如果能够确定高次剩余码幂等生成元，求这些幂等生成元与xn-1最大公因式就可得到高次剩余码生成多项式而不用分解xn-1[1]。本文给出了二元域F2上三次和四次剩余码的幂等生成元表达式。

2 预备知识

定义1[5]如果方程xt≡2(modp)有解，则称2是模 p的一个t次剩余。

定义3[1]设p是奇素数，若e(x)∈F2[x]/(xp-1)满足 e(x)2≡e(x)(mod(xp-1))则称e(x)为F2[x]/(xp-1)的幂等元。能生成循环码的幂等元e(x)称为幂等生成元。

定义4[8]设C是有限域Fq上长为n的循环码，又设α是 Fq的扩域上n次本原单位根，Z={αi|i∈T}是C的根集合，则称T是C的定义集。

定义5[8]设 a是整数并且 (a，n)=1，定义映射 iμa≡ia(modn)，i∈{0，1，…，n-1}，将此定义延伸到 Fq[x]/(xn-1)使得 f(x)μa≡ f(xa)(modxn-1)，f(x)∈ Fq[x]/(xn-1)。

引理4[8]设C是有限域Fq上长为n并且以T为定义集的循环码，a是整数并且(a，n)=1，a-1是a模n的乘法逆，则a-1T(modn)是循环码Cμa的定义集。

引理5[8]设e(x)是循环码C的幂等生成元，则e(x)μa是循环码Cμa的幂等生成元。

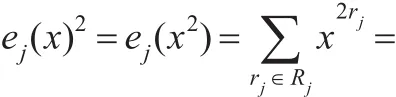
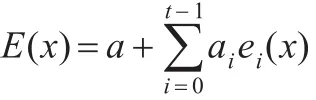
证明设E(x)是t次剩余码C的幂等生成元，则C的定义集为某个Rl或={0}∪Rl。由于每个Ri都是分圆陪集之并，故可设Ri=Ci1∪Ci2∪…∪Civi，其中Cik都是分圆陪集，i∈{0，1，…，t-1}。由 R0∪R1∪…∪Rt-1={1，2，…，n-1}和引理6可设：

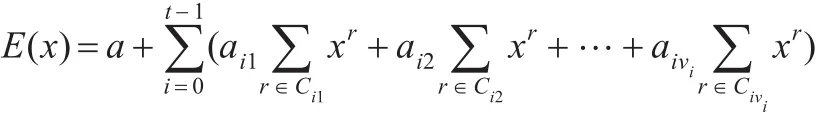
因为 Ri={ρtk+i∈FP|k∈Z}，其中 i∈{0，1，…，t-1}，故不妨设 Ci1={ρi，2ρi，…} 。如果 Cif={ρtf+i，2ρtf+i，…} ，则取d=ρtf∈R0。于是 dCi1=Cif从而

又因为

3 三次和四次剩余码的幂等生成元

情况1 e0(α)，e1(α)，e2(α)，e3(α)之中有一个为1，另外三个为 0。设 ei(α)=1,ei+1(mod4)(α)=ei+2(mod4)(α)=ei+3(mod4)(α)=0 。令e(x)=ei+1(mod4)(x)+ei+2(mod4)(x)+ei+3(mod4)(x)。显然e(x)是幂等元。

4 结束语

本文给出了二元域上三次和四次剩余码的幂等生成元表达式。求解这些幂等生成元与多项式xn-1最大公因式就可得到二元域上三次和四次剩余码的生成多项式。而在有限域上求解两个多项式的最大公因式可用已有的计算机软件如Maple，Matlab等来解决，从而可得到具体的二元域上三次和四次剩余码。如何确定更高次剩余码的幂等生成元是一个有待研究的问题。

[1]Macwilliams F J，Sloane N J A.The theory of error-correcting codes[M].Amsterdam，the Netherlands：North-Holland，1977.

[2]Pless V，Qian Z.Cyclic codes and quadratic residue codes over[J].IEEE Trans on Inform Theory，1996，42（5）：1594-1600.

[3]卢慧敏，董学东，李选海.Z2k上的二次剩余码[J].应用数学学报，2008，31（2）：257-265.

[4]董学东，高洁，杨丽.关于三次剩余码[J].辽宁师范大学学报，2002，25（1）：1-2.

[5]高洁.关于e次剩余码[D].大连：辽宁师范大学，2002.

[6]高丽，李体政，封利锋，关于四次剩余码及其推广[J].天津师范大学学报，2003，23（1）：37-39.

[7]朱士信，陈安顺.域F2上的三次剩余码[J].电子学报，2008，36（12）：2312-2314.

[8]Huffman W C，Pless V.Fundamentals of error correcting codes[M]. Cambridge：Cambridge University Press，2003：138-144.

二元域上三次和四次剩余码的幂等生成元

董学东1，李文杰2，张 妍3

DONG Xuedong1,LI Wenjie2,ZHANG Yan3

1.College of Information Engineering,Dalian University,Dalian,Liaoning 116622,China
2.Middle School Attached to Chifeng College，Chifeng,Nei Mongol 024000,China
3.School of Mathematics,Liaoning Normal University,Dalian,Liaoning 116029,China

The generating polynomials of higher degree residue codes over finite fields are factors of the polynomialxn-1. Generally speaking,it is difficult to factor the polynomialxn-1over finite fields.This paper gives generating idempotents of cubic and quartic residue codes over the fieldF2.As a result,the generating polynomials of cubic and quartic residue codes over the fieldF2can be obtained by computing the greatest common divisors of these generating idempotents and the polynomial xn-1with computer software such as Matlab and Maple。

generating idempotent;residue code;cyclic code

有限域上高次剩余码的生成多项式都是多项式xn-1的因式。针对多项式xn-1在有限域上分解的困难性，给出了二元域F2上三次和四次剩余码的幂等生成元表达式。利用计算机软件求解该幂等生成元与xn-1最大公因式就可得到三次和四次剩余码生成多项式而不用分解xn-1。

幂等生成元；剩余码；循环码

A

TN911.22

10.3778/j.issn.1002-8331.1203-0577

DONG Xuedong,LI Wenjie,ZHANG Yan.Generating idempotents of cubic and quartic residue codes over fieldF2. Computer Engineering and Applications,2013,49（11）：41-44.

国家自然科学基金（No.10171042）；辽宁省教育厅高校科研项目（No.L2010234）。

董学东（1961—），男，博士，教授，研究领域：编码密码学；李文杰（1985—），女，硕士，研究领域：编码密码学；张妍（1978—），女，博士研究生，讲师，研究领域：编码密码学。E-mail：dongxuedong@dl.cn

2012-03-26

2012-06-19

1002-8331（2013）11-0041-04