不锈钢点焊车体结构稳定性分析及局部焊点布局优化

谢素明，穆伟，高阳

(1.大连交通大学 交通运输学院，辽宁 大连 116028;2.中国北车集团 长春轨道客车股份有限公司技术中心，吉林 长春 130062)*

0 引言

不锈钢点焊车因其具有高耐腐蚀性、车体自重轻、维修费用以及运营成本相对较低等优点而逐渐成为国内外轨道交通轻量化车体的主流［1］.不锈钢车体承载大部件主要由各类薄壁梁借助点焊连接组成，因承载部件厚度很小及某些区域的焊点布置存在冗余和不足，致使车体结构局部易发生失稳现象［2］.

目前，不锈钢点焊车的研究主要集中在车体制造和点焊工艺等方面［3-4］.对不锈钢点焊车结构稳定性数值仿真的研究较少，王英琳等对40 t轴重不锈钢矿石专用敞车车体进行了结构稳定性的研究，通过地板加筋增加地板刚度，提高了车体结构的稳定性［5］.

本文以某不锈钢点焊地铁车为研究对象，建立了用于分析点焊车体结构稳定性分析的有限元模型.依据EN12663-2010标准［6］，对车体结构稳定性进行了分析与评价.为提高不锈钢点焊车体结构稳定性，基于子结构技术［7］和变密度法［8］对车体失稳部位进行了结构改进和焊点布局优化.

1 结构稳定性分析算法原理

薄板在其边界上承受的纵向载荷超过某一数值(即临界载荷)时，其平面平衡状态将变得不稳定.此时，薄板再承受横向干扰力而弯曲之后，即使去除干扰力，它也无法再恢复初始状态，称这种现象为薄板屈曲(或失稳).四边简支的矩形薄板的两对边受有单位长度均布压力Px(参见图1)时，其屈曲临界载荷的推导如下.

图1 四边简支矩形薄板

由弹性力学平面问题的理论，薄板中面内力为:

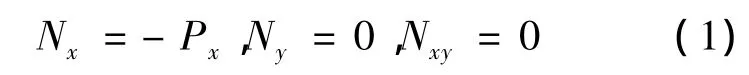
又薄板的屈曲微分方程为:

将式(1)带入式(2)得:

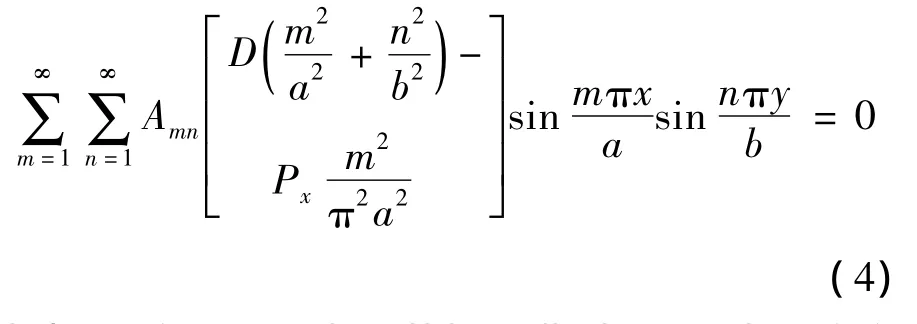
式中，m和n分别表示薄板屈曲以后沿x与y方向的正弦半波数目.当Px逐渐增大时，则由上式可导出纵向载荷Px的临界值:

上述通过求解薄板屈曲微分方程函数形式的非零解，获得临界载荷的精确值，仅适用于薄板结构十分简单的情况.对复杂产品结构(如不锈钢点焊车体)的稳定性分析，通常采用有限元方法求解结构的屈曲微分方程.基于有限元法的结构稳定性平衡方程为:

式中，KE为结构刚度矩阵;δ为位移向量;F为载荷向量;Kσ为结构中现存的内力对弯曲刚度的影响矩阵，依赖于单元形状、位移和应力状态，与材料性质无关.引入表示屈曲时随遇平衡的虚位移，且假设结构在弹性范围内，可推出:

式中，λ是初始外力P0的系数.

方程(7)所表示的屈曲方程是一广义特征值问题，使其有非零解的λ即为该方程的特征值(或屈曲因子)，与其对应的特征向量即为屈曲振型，初始外力P0乘以λ便是屈曲时的临界载荷.

2 车体结构稳定性分析

不锈钢点焊车体是典型的薄壁筒型整体承载的点焊传力结构，由底架、左右侧墙、车顶、端墙等模块组成.车体在承受外部载荷后，载荷通过数万焊点将力传递到车体各部位，由此产生车体各处的变形与应力.车体主要承载部件采用SUS301L系列高强度不锈钢材质，只在底架边梁与牵枕缓部位采用碳钢材质，车体所用材料性能参数见表1.

表1 车体材料性能参数

不锈钢点焊车体结构中，点焊焊核自身的尺寸非常小，在建立整车车体有限元模型时，可以将它们视为整体坐标系下的一个“点”，在外部载荷作用下，结构内各部件主要依靠这些“点”来传力.此外，考虑到不锈钢点焊车焊点的数量，基于ANSYS软件，采用梁单元beam188模拟焊点;车体薄壁部件主要离散为四节点等参数单元shell181;采用质量单元mass21来模拟设备质量，并通过柔性元rbe3模拟与车体的连接关系.图2给出了某不锈钢点焊地铁车体稳定性分析的有限元模型，单元总数为 1151798，结点总数为1150694.

图2 用于稳定性分析的车体有限元模型

依据EN12663-2010标准，不锈钢点焊地铁车体稳定性分析的压缩载荷为800 kN，施加在车钩座处.车体结构稳定性的临界载荷Pcr与外载荷P0之比λ应大于等于1.5，即:

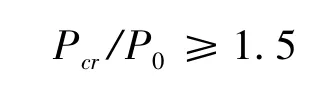
不锈钢点焊车体结构稳定性分析的部分结果见表2，表中力的单位为kN.车体侧墙发生失稳部位和车体第一阶屈曲振型如图3所示.结合表2和图3可以看出:车体结构失稳区域主要是侧墙的窗下侧墙板部位，第一阶屈曲因子小于1.5，仅为0.882 736.所以，应对窗下侧墙板部位增加刚度，以提高其稳定性.

表2 车体结构稳定性分析部分结果

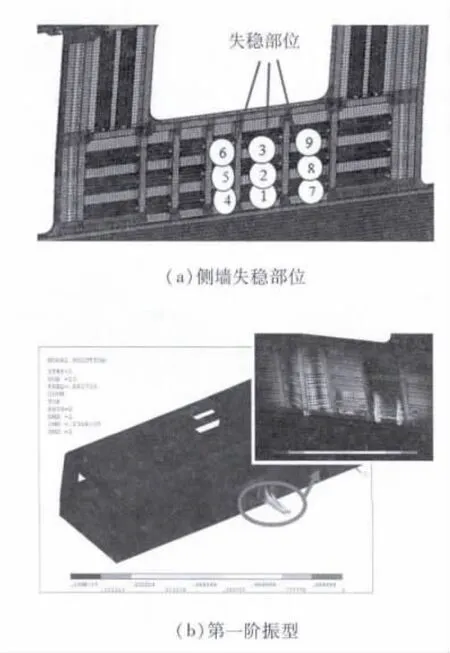
图3 车体失稳部位及第一阶屈曲振型

3 车体局部焊点布局优化

基于变密度法，对车体侧墙分区域焊点拓扑优化的基本思路是:对给定初始焊点分布空间，通过拓扑优化计算后，去除冗余焊点，保留关键焊点.车体侧墙分区域焊点布局优化之前，对侧墙区域1局部加强的厚度为1 mm的两个帽型梁与侧墙板的焊点布置的间隔为5 mm，参见图4.设计变量取为设计空间的单元密度(即焊点单元CWELD作为拓扑变量);优化目标是:在800 kN压缩载荷下，设计空间应变能最小;约束条件是:优化后设计空间体积不能超过原有体积的40%.

图4 侧墙区域1优化前局部焊点分布空间示意

为了提高车体焊点布局优化的效率，利用子结构技术把需要优化区域提出来单独优化，而其他不需要优化的部分则作为两个子结构，1/4车体的子结构划分如图5所示.

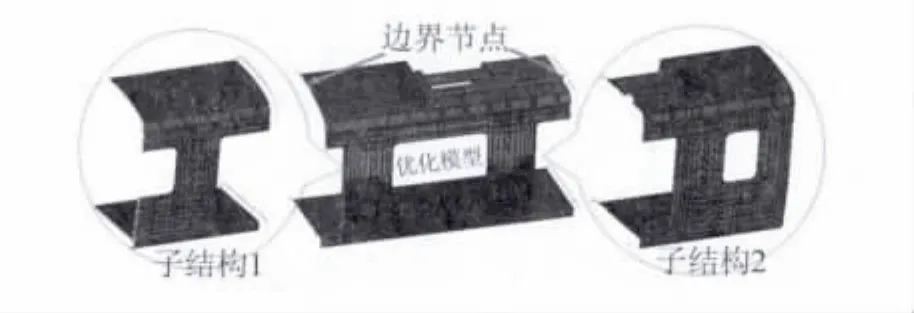
图5 1/4车体的子结构划分示意

利用 Altair OPTISTRUCT 软件［9］，基于变密度法和子结构技术的车体局部焊点布局优化的流程如图6所示.

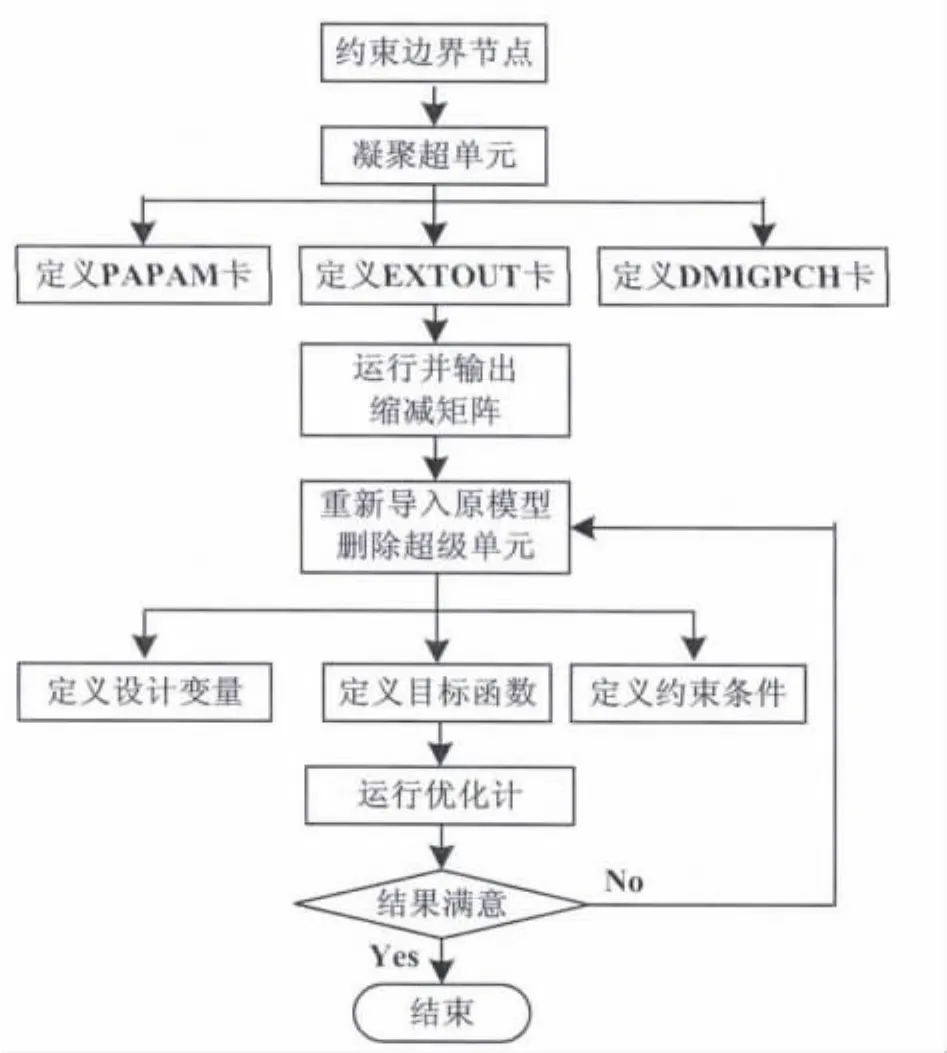
图6 车体局部焊点布局优化的流程图

车体侧墙区域1局部焊点优化后的焊点分布如图7(a)所示，图中黄色部分为高密度单元.考虑焊点间距不能过小以免彼此相互影响严重致使焊点失效，以及焊点最小间距的工艺要求，在拓扑优化的基础上，经人工修匀处理，最终区域1的焊点布置如图7(b)所示.

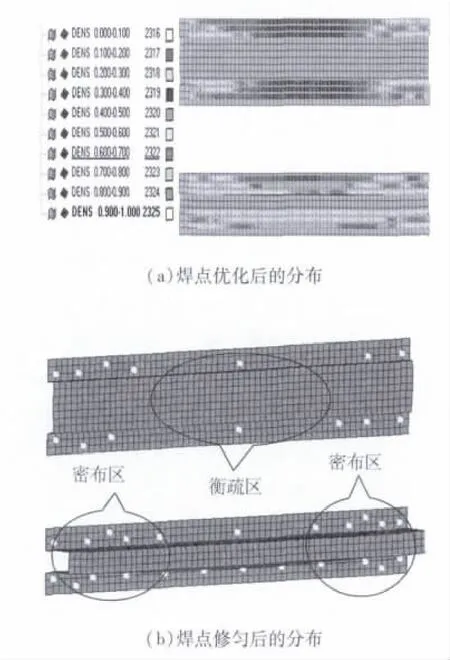
图7 车体侧墙区域1焊点分布

图8 车体侧墙区域1～9焊点分布

将优化后的模型导入ANSYS中重新进行结构稳定性分析，原车体侧墙局部失稳区域1直到屈曲因子λ达到1.5以后仍未发生失稳.所以，将该设计方案进行推广，即侧墙区域1、2、3、4、5、6、7、8、9的焊点按同样的方法进行拓扑优化.优化后模型的焊点分布和圆整修匀后的焊点分布如图8所示.结构改进和侧墙焊点布局优化的最终车体的结构稳定性分析结果表明:车体窗下侧墙部位的第一阶屈曲振型参见图9，对应的屈曲因子为1.553.

图9 最终车体侧墙第一阶屈曲振型

4 结论

在EN12663-2010标准中载荷作用下，对不锈钢点焊车体结构稳定性数值分析结果表明:车体侧墙窗下区域是其失稳部位，第一阶屈曲因子仅为0.882736.通过对失稳部位结构增加刚度设计，以及采用子结构技术和基于变密度法对车体局部焊点布置进行拓扑优化设计，最终车体侧墙结构的屈曲因子为1.553，满足EN12663-2010标准中对结构稳定性的要求.这种借助增加结构局部刚度和优化焊点布局提高结构稳定性的设计手段，可推广到不锈钢点焊车体其它部位的抗失稳设计中.

［1］王洪亮，王亭，徐国成.不锈钢城轨客车车体电阻点焊质量监控［J］.焊接技术，2010，39(10):60-62.

［2］黄志宏，许彦强.不锈钢车体结构设计及仿真分析要点［J］.铁道车辆，2012，50(6):14-18.

［3］王雪芳，蒋正光，袁立祥.城轨车辆不锈钢车体制造技术研究［J］.电力机车与城轨车辆，2012，35(3):76-78.

［4］彭章祝，吴志明.城轨不锈钢车体制造焊接工艺研究［J］.现代机械，2012(3):1-3，11.

［5］王英琳，许平.40t轴重不锈钢矿石专用敞车车体.铁道车辆，2008，46(11):4-7.

［6］英国标准学会.BS EN 12663-1:2010铁路车辆车体的结构要求(第一部分:机车和客运车辆)［S］.英国:［s.l.］，2010.

［7］周素霞，谢云叶，谢基龙，等.基于子结构法的重载凹底平车底架的固有动态特征分析［J］.铁道学报，2011，8(33):28-32.

［8］李好.基于变密度法的连续体结构拓扑优化方法研究［D］.武汉:华中科技大学，2011.

［9］唐涛.基于 Hypermesh/OptiStruct的发动机支架结构拓扑优化设计［J］.制造业自动化，2011，12(33):1-4.