某些差分方程的值分布

蒋业阳，陈宗煊

(华南师范大学数学科学学院，广东广州510631)

1 引言与结果

本文使用值分布理论的标准记号［1－2］，并用σ(f)表示亚纯函数f(z)的增长级，λ(f)、λ(1/f)分别表示亚纯函数f(z)零点以及极点的收敛指数，用τ(f)表示f(z)的不动点收敛指数，其定义为τ (f)=

在20 世纪初期，复域差分方程理论的研究缓慢.到了20 世纪七、八十年代，由于Nevanlinna 理论的引入，发展了复域差分方程理论. 最近十来年，随着一系列差分模拟定理的建立，复域差分和差分方程又成了研究热点［3－14］.ABLOWITZ 等［3］研究了方程

和

利用经典的Malmquist 定理，获得了下面2个定理:

定理1［3］假设系数ai(z)，bj(z)(i =0，…，p;j=0，…，q)为多项式，如果差分方程(1)有一个有限级的亚纯解，那么d=max(p，q)≤2.

定理2［3］假设系数ai(z)，bj(z)(i =0，…，p;j=0，…，q)为多项式，如果差分方程(2)有一个有限级的亚纯解，那么d=max(p，q)≤2.

HEITTOKANGAS 等［12］推广了定理1 和定理2，得到了类似的结论:

定理3［12］设c1，…，cnC，系数ai(z)，bj(z)(i=0，…，p;j=0，…，q)为有理函数，若

有一个有限级的亚纯解，则d=max(p，q)≤n.

定理4［12］设c1，…，cnC，系数ai(z)，bj(z)(i=0，…，p;j=0，…，q)为有理函数，若

有一个有限级的亚纯解，则d=max(p，q)≤n.

HALBURD 等［11］利用值分布理论和极点限制的方法，从差分方程

分离出差分Painlevé II 方程，获得了下面的定理:

定理5［11］设有理数R(z，y)的分母关于2个变量都有至少2个相互判别的根，如果二阶差分方程(3)允许有一个非有理的有限级亚纯解，使得存在一个常数c≥1，满足对于足够大的r，有

成立，那么方程(3)是一个形如

的Painlevé II 方程，其中λ，μ 和ν 是常数.

注1 如果y 在点z=z0处有一个极点，y(z0±1)= ±ε(ε= ±1)，就说在z0处的奇点是型I 的;如果y(z0±1)=∓ε，就说是型II 的.用ˉnI(r，y)表示在圆域内型I 极点的个数(不计重数). 类似的，用(r，y)表示在圆域内型II 极点的个数(不计重数).

由上可知，差分Painlevé I 和II 方程是重要类型的差分方程，它们是微分和离散Painlevé I、II 方程的发展.CHEN 等［6］研究了差分Painlevé I、II 方程的亚纯解的一些性质，得到了以下定理:

定理6［6］设a，b，c 是满足ac≠0 的常数，如果f(z)是差分Painlevé II 方程

的一个有限级超越亚纯解，那么

(i)f(z)至多有一个非零有限Borel 例外值;

(iii)f(z)有无穷多个不动点，且满足τ (f)=σ(f).

我们提出一个问题:如果定理6 中的二阶差分方程推广到高阶差分方程的情况又是怎样?本文回答了这个问题，并得到了下面的结果:

定理7 设A，B，C 是满足AC≠0 的常数，cj(j=如果f(z)是差分方程

的一个有限级超越亚纯解，那么

(i)f(z)至多有一个非零有限Borel 例外值;

(iii)f(z)有无穷多个不动点，且满足τ (f)=σ(f).

定理8 设A，B，C 是满足AC≠0 的常数，cj(j=如果f(z)是差分方程

的一个有限级超越亚纯解，那么

(i)f(z)至多有一个非零有限Borel 例外值;

(iii)f(z)有无穷多个不动点，且满足τ (f)=σ(f).

定理9 设α，β，γ 是满足αγ≠0 的常数，如果f(z)是差分方程

的一个有限级超越亚纯解，那么

(i)f(z)至多有一个非零有限Borel 例外值;

(iii)f(z)有无穷多个不动点，且满足τ (f)=σ(f).

2 证明所需的引理

为证定理，需要以下引理，其中引理1 和引理3是Clunie 型定理的差分模拟.

引理1［8，13］假设f(z)是P(z，f)=0 的一个非常数有限级亚纯解，其中P(z，f)是关于f(z)的一个差分多项式，如果对于一个满足的亚纯函数a(z)，有P(z，a)≢0，那么在可能除去一个具有有穷对数测度的集合外成立S(r，f).

引理2［9］设A，B，C 是满足AC≠0 的常数，cj如果f(z)是差分方程(4)的一个有限级超越亚纯解，那么

(i)f(z)有无穷多个不动点，且满足τ (f)=σ(f);

(ii)λ(f)=σ(f).

证明 设f(z)是差分方程(4)的一个超越亚纯解，且σ(f)＜∞.

(i)令g(z)=f(z)－z，把f(z)=g(z)+z 代入方程(4)，可得

由上式得

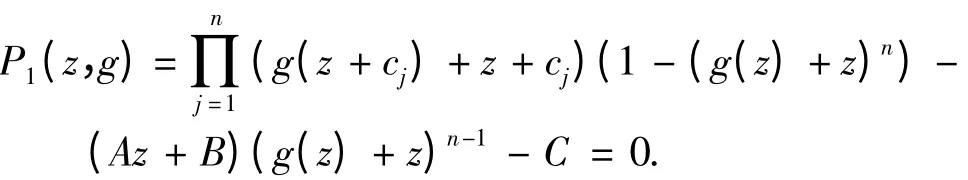
由上式可得

由引理1 和上式得，在可能除去一个具有有穷对数测度的集合外有

从而在可能除去一个具有有穷对数测度的集合外有

从而有

(ii)由式(4)有

由上式和引理的假设条件有P2(z，g)=－C≢0. 由引理1 得m(r，1/f)=S(r，f)在可能除去一个具有有穷对数测度的集合外成立. 因此

也在可能除去一个具有有穷对数测度的集合外成立. 从而由上式有λ(f)=σ(f).

引理3［13］设f(z)是形如H(z，f)P(z，f)=Q(z，f)的差分方程的一个有限级超越亚纯解，其中H(z，f)是f(z)和其位移算子的次数为n 的差分多项式，P(z，f)，Q(z，f)也是差分多项式，且Q(z，f)的次数≤n. 那么对于任意的ε ＞0，有m(r，P(z，f))=O(rσ－1+ε)+S(r，f)在可能除去一个具有有穷对数测度的集合外成立.

文献［9］指出下面的引理4 成立，或由文献［10］的引理2.1 的证法，易证引理4.

引理4 设f(z)是非常数有限级亚纯函数，c≠0 是任意复常数，那么有

注2 文献［7］证明了一个类似的结果.设f(z)是满足λ(1/f)=λ ＜∞的一个亚纯函数，给定η≠0，那么对于任意的ε ＞0，有

引理5 设A，B，C 是满足AC≠0 的常数，cj(j =1，…，n)C－{0}，n≥2.如果f(z)是差分方程(4)的一个有限级超越亚纯解，那么f(z)有无穷多个极点，且满足λ(1/f)=σ(f).

证明 设f(z)是差分方程(4)的一个满足σ(f)＜∞的超越亚纯解，方程(4)可变形为，

其中

由式(7)和引理3，对任给的ε ＞0，存在一个具有有穷对数测度的集合E⊂(1，∞)，使得［0，1］∪E 时，有

其中σ=σ(f).由方程(4)有

应用Valiron－ Mohon'kon 引理［2］到上式可得T(r，P)=nT(r，f)+S(r，f).故由式(8)得

和

由引理4，有

因此，综合式(9)～(11)得到

用证明引理2 和引理4 类似的方法，可以证明下面2个引理:

引理6 设A，B，C 是满足AC≠0 的常数，cj(j =1，…，n)C－{0}，n≥2.如果f(z)是差分方程(5)的一个有限级超越亚纯解，那么:

(i)f(z)有无穷多个不动点，且满足τ (f)=σ(f);

(ii)λ(f)=σ(f).

引理7 设A，B，C 是满足AC≠0 的常数，cj(j =1，…，n)C－{0}，n≥2.如果f(z)是差分方程(5)的一个有限级超越亚纯解，那么f(z)有无穷多个极点，且满足λ(1/f)=σ(f).

引理8［2］设fj(z)(j =1，…，n;n≥2)均为亚纯函数，gj(z)(j=1，…，n)都是整函数，且满足

(ii)当1≤j ＜k≤n 时，gj(z)－gk(z)均不是常数;

(iii)当1 ≤j ≤n，1 ≤h ＜k ≤n 时，T(r，fj)=o{T(r，egh－gj)}(r→∞，rE)，其中E⊂(1，∞)是一个具有有限测度或具有有穷对数测度的集合，那么fj(z)≡0 (j=1，…，n).

3 定理的证明

定理7 的证明 由引理2 和引理5 知，结论(ii)和(iii)成立.

假设f(z)是差分方程(4)的一个超越亚纯解，且0 ＜σ(f)＜∞. 由(ii)知，0，∞不是f(z)的Borel例外值.假设α 和β(≠0，α)是f(z)的2个Borel 例外值. 令

那么σ(g)=σ(f)，λ(g)=λ(f－α)＜σ(g).因此，g(z)可以重写为

其中d (≠0)是一个常数，m (≥1)是一个整数，h(z)是一个满足σ(h)≤σ(g)=m 的亚纯函数.由式(12)和式(13)，有

和

其中hj(z)=. 把式(14)、(15)代入式(4)，可以得到

其中

由引理8 和式(16)，得F2n≡F2n－1≡…≡F1≡F0≡0.因由式(17)和F2n≡0，所以(Az+B)βn－1+C－βn(1－βn)≡0.由定理的假设条件AC≠0 和例外值β≠0 的假设，可知是一个矛盾.从而f(z)至多有一个Borel 例外值.再应用引理2 和引理5，定理7 的结论(i)成立.

定理8 的证明 由引理6 和引理7 知，结论(ii)和(iii)成立.

下面证明结论(i).

设f(z)是差分方程(5)的一个超越亚纯解，且0 ＜σ(f)＜∞.由结论(ii)知，0，∞不是f(z)的Borel例外值.假设α 和β(≠0，α)是f(z)的2个Borel 例外值.用与定理7 证明相类似的方法，有式(12)～(15).把式(14)、(15)代入式(5)，得

其中

因此，由引理6 和式(18)，有

由定理的假设条件AC≠0 和例外值β≠0 知，上式矛盾.从而f(z)至多有一个Borel 例外值.再由引理6 和引理7，定理8 的结论(i)成立.

定理9 的证明 假设f(z)是方程(6)的一个有理解，且有极点z1，…，zk.从而可以假设

分别是f(z)在zj的主要部分，其中ajλj，…，aj1均是常数，ajλj≠0.因此，f(z)可以表示为

其中b0，…，bs均是常数.

首先断言b0=… =bs=0. 假设bs≠0 (s≥1).对足够大的z，由式(20)有

差分方程(6)可以变形为

把式(21)代入式(22)得

因为bs≠0 和s≥1，对足够大的z，上式是个矛盾.

现在假定b1=…=bs=0，b0≠0.对足够大的z，有

由方程(6)有

把式(23)代入式(24)得

因为α≠0 和b0≠0，对足够大的z 上式也是矛盾的.从而bs=… =b0=0. 由式(20)和b0=… =bs=0，f(z)可以写为

其中P(z)=pzm+pm－1zm－1+… +p0，Q(z)=qzn+qn－1zn－1+ … + q0，且deg Q = n ＞deg P = m，p≠0，pm－1，…，p0和q ≠0，qn－1，…，q0均为常数. 把式(25)代入式(6)得

因为αγ≠0，比较上述方程左右两边的次数，得出矛盾.从而方程(6)的所有亚纯解都是超越的.

再由定理7，结论(i)、(ii)和(iii)成立.

［1］HAYMAN W K. Meromorphic functions［M］. Oxford:Clarendon Press，1964.

［2］LAINE I. Nevanlinna theory and complex differential equations［M］.Berlin:Water de Gruyter，1993.

［3］ABLOWITZ M，HALBUD R G，HERBST B.On the extension of Painleve property to difference equations［J］.Nonlinearity，2000，13:889－905.

［4］BERGEWEILER W，LANGLEY J K. Zeros of differences of meromorphic functions［J］. Math Proc Cambridge Philos Soc，2007，142:133－147.

［5］CHEN Z X，SHON K H. On zeros and fixed points of differences of meromorphic functions［J］. J Math Anal Appl，2008，344:373－383.

［6］CHEN Z X，SHON K H. Value distribution of meromorphic solutions of certain difference Painlevé equations［J］.J Math Anal Appl，2010，364:556－566.

［7］CHIANG Y M，FENG S J.On the Nevanlinna characteristic of f(z + η)and difference equations in the complex plane［J］.Ramanujan J，2008，16:10－129.

［8］HALBURD R G，KORHONEN R. Difference analogue of the lemma on the logarithmic derivative with applications to difference equations［J］.J Math Anal Appl，2006，314:477－487.

［9］HALBURD R G，KORHONEN R.Meromorphic solution of difference equation，integrability and the discrete Painlevé equations［J］.J Phys A，2007，40:1－38.

［10］HALBURD R G，KORHONEN R. Finite－ order meromorphic solutions and the discrete Painlevé equations［J］.Proc Lond Math Soc，2007，94:443－474.

［11］HALBURD R G，KORHONEN R. Existence of finite－order meromorphic solutions as a detector of integrabilityin difference equations［J］.Phys D，2006，218:191－203.

［12］HEITTOKANGAS J，LAINE I，RIEPPO J，et al.Complex difference equations of Malmquist type［J］. Comput Methods Funct Theory，2001，1:27－39.

［13］黄志波，李倩. 一类差分Painlevé I 方程的值分布［J］. 华南师范大学学报:自然科学版，2011(3):15－18.

［14］LAINE I，YANG C C.Clunie theorems for difference and q－difference polymials［J］.J Lond Math Soc，2007，76:556－566.