基于非迭代与迭代法联合估计的七参数坐标转换方法研究*

谭骏祥 李少达 杨容浩

(成都理工大学地球科学学院，成都 610059)

1 引言

空间直角坐标转换常采用七参数模型［1］，针对七参数模型的参数求解，大致分为迭代解和非迭代解法两类。根据旋转矩阵求解方法不同，非迭代解法一般采用SVD 分解法［2］、正交矩阵法［3］、单位四元数法［4］、对偶四元数法［5］等;根据旋转矩阵表达方式不同，迭代解法常使用欧拉角形式［6］、正交矩阵形式［7］和四元数形式［8］。

在已有七参数模型求解方法的基础上，本文首先简述了迭代解法与非迭代解法，然后通过实测数据对比分析了两类解法的优缺点，进而提出联合两类解法来估计七参数，以期实现任意旋转角度的稳健高精度空间直角坐标转换。

2 模型的表示与算法评价

2.1 模型表示

据研究，一般化的三维坐标转换非线性模型为:

式中，vS=［x，y，z］T和vT=［X，Y，Z］T分别表示待转换坐标和目标坐标，vθ=［ΔX，ΔY，ΔZ］T为平移向量，x=［ΔX，ΔY，ΔZ，s，φ，θ，γ］T为七参数向量，s 为尺度参数，R 为旋转矩阵。R 绕z、x、y 轴旋转φ、θ、γ后组成的序列为:

假定e 为随机误差且e ～N(0，δ2)，则两个坐标系中相对应的控制点的关系为:

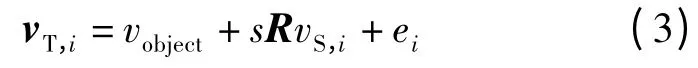
式中i=1，2，…，M，M 为控制点的个数。

为了减小求解过程中坐标值的有效位数，提高计算过程的精度，对模型进行重心化处理，得

2.2 算法评价

使用均方根误差(RMSE，Root Mean Square Error)度量转换后坐标与目标坐标的接近程度，即

由于七参数的真值未知，我们根据转换残差来判断求解的准确性。若RMSE 超过限差值e 时，即RMSE ＞e，则认为七参数的估计值错误，模型求解不准确。需要指出的是，实际坐标转换中的尺度参数估值常接近1，否则，也会认为求解错误。

3 模型的最小二乘估计

3.1 非迭代解法

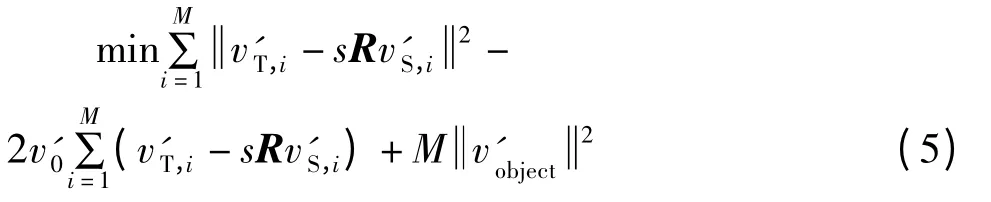
使用式(5)进行非迭代解法估计参数的分步求解，求解过程为:求尺度参数→旋转矩阵→平移向量。其中尺度参数s 的求解式为:

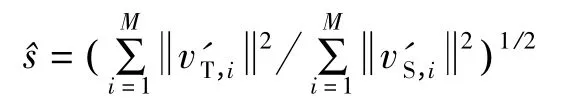
求解旋转矩阵R 常用的是单位四元数法，根据单位四元数法，先计算N

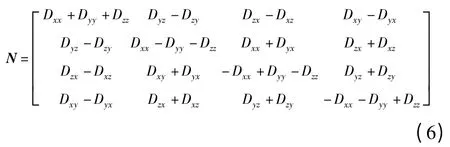
根据最大特征值对应的单位特征向量q=［q0，q1，q2，q3］，

3.2 迭代解法

式(4)按泰勒级数展开取至1 次项得:

式中v=Bx－l，其中v=［dvT，1，dvT，2，…，dvT，M］T，B=［B1，B2，…，BM］T，Bi=［I3，RvS，i，svS，i］，l=［l1，l2，…，lM］T，li=vT，i－v0－sRvS，i，I3表示3 阶单位矩阵，x 为所求未知数改正数。由于R 有欧拉角、正交矩阵和四元数等3 种表达形式，而欧拉角形式有3个，正交矩阵形式有9 个，四元数形式有4 个。而表达旋转只需要3 个必要参数，因此正交矩阵形式需要6 个约束条件，四元数形式只需1 个约束条件。

1)正交矩阵形式

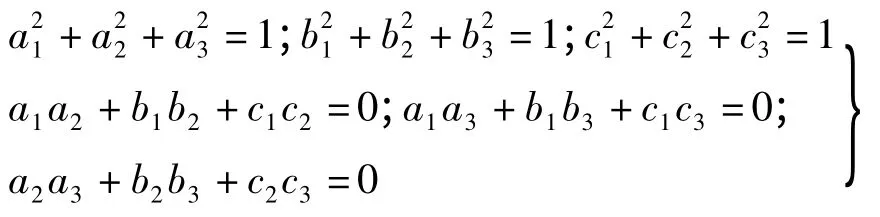
2)四元数形式

设单位四元数q=［a，b，c，d］，构造旋转矩阵为:

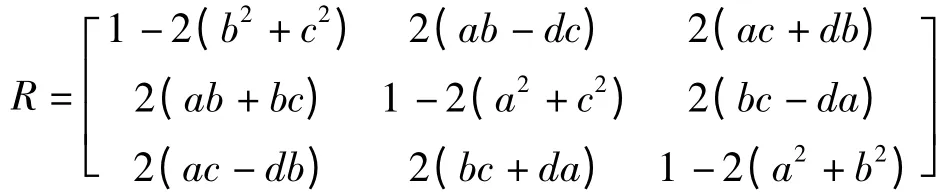
约束条件为a2+b2+c2+d2=1。

式(8)表示的七参数线性化模型使用间接平差方法可求得x=(BTB)－1BTl。由于按泰勒级数展开进行线性化会产生误差，因此采用迭代运算，迭代过程直至迭代前后两次x 之差小于某一微小量为止。

4 算法对比

为了验证七参数求解方法的精度和准确性，坐标转换实验采用两组实测数据进行。第一组数据的控制点转换前后坐标系分别为WGS84 和西安80 坐标系(表1)，覆盖范围比较大，最远两控制点间隔约80 千米，但两个坐标的旋转角度相对较小。第二组数据的控制点来自具有一定重叠度的两站激光扫描数据(表2)，范围很小，但旋转角度比较大。

表1 第一组数据的控制点坐标(单位:m)Tab.1 Coordinates of control points of the first set data(unit:m)

表2 第二组数据的控制点坐标(单位:m)Tab.2 Coordinate of control points of the second set data(unit:m)

实验中，非迭代解法不需要设置参数;迭代求解中7 参数的近似值是未知的，分别设置v0、u 和旋转角度的初始值为［0，0，0］T、1 和［0，0，0］T，设置最大迭代次数为300(表3、4)。

从表3 看，对于小角度的坐标转换，非迭代解法与迭代解法均能求得转换参数的正确估计值，其中非迭代解法的正交矩阵法的迭代次数最少，求解精度最高。从表4 看，对于角度较大的坐标转换，非迭代解法仍然能求得转换参数的正确估值，可迭代解法不能够收敛至正确的值。由表3、4 可见:非迭代解法不需要迭代，均能收敛至正确的解，但精度可能不如迭代解法高;迭代解法需要迭代求解，可收敛至更高精度，但当旋转角度过大时易收敛至错误解。

5 联合估计七参数

非迭代解法采用分步求解七参数，不需要迭代，在大小旋转角度下均能获得正确估值，但没有考虑同时包含七参数的误差模型，精度可能较低;迭代解法采用同时求解七参数，并通过迭代的方式逐步逼近最佳待求解参数，不足之处在于迭代的收敛性易受初始值的影响，不适用于大旋转角的坐标转换。针对两类解法的优缺点，提出联合两类解法来估计七参数，具体步骤为:

表3 第一组数据的求解结果对比Tab.3 Comparison of solutions of the first set data

表4 第二组数据的求解结果对比Tab.4 Comparison of solutions of the second set data

1)使用非迭代解法求解转换前坐标vS至转换后坐标vT的初始转换参数xini，包括旋转矩阵Rini(或旋转角度φini，θini，γini)、尺度参数sini和平移向量v0ini;

2)根据式(1)，利用xini将vS转换至vTini，此时vTini与vT已经相当接近;

3)设置v0、u 和旋转角度的初始值为［0，0，0］T、1 和［0，0，0］T，利用迭代解法求解vTini至vT的转换参数xend;

4)根据式(1)，利用xend将vTini转换至vT，完成坐标转换。

求解中，分别联合常用的非迭代解法单位四元数法与三种迭代解法估计七参数，即将单位四元数法的解作为迭代解法的初始值进行迭代求解，于是产生三种联合解法。利用表1、2 数据的联合求解结果见表5、6。

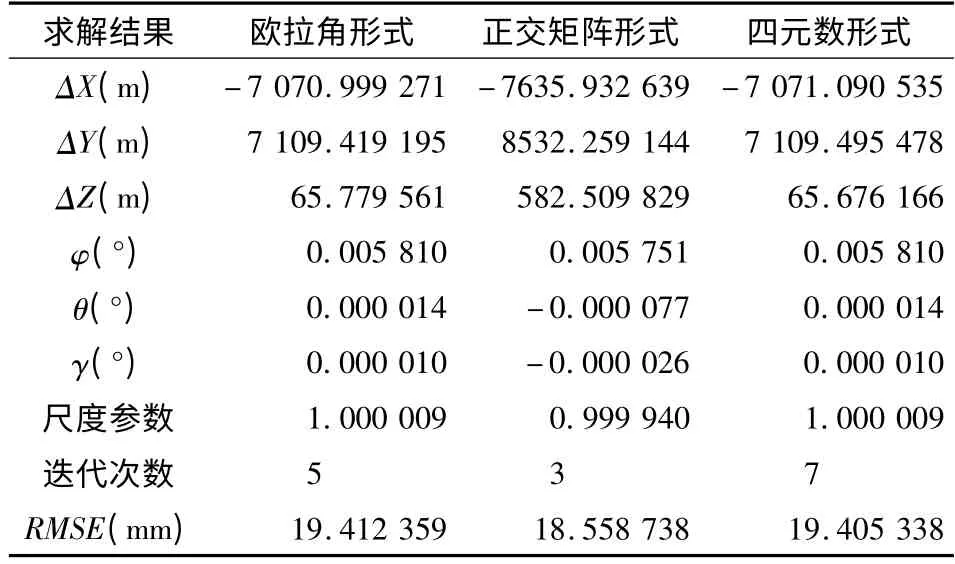
表5 第一组数据的联合求解结果Tab.5 The results of combined estimation for the first set of data

表6 第二组数据的联合求解结果Tab.6 The results of combined estimation for the second set of data

由表5、6 可见，两组数据均能获得正确的结果，体现了此方法的正确性。其中，正交矩阵的迭代次数最少，并且能获得最高的转换精度，四元数形式次之，欧拉角的效果最差。与表3、4 相比较，联合解法的精度几乎高于非迭代解法，在大旋转角度下也能获得正确的估计值。

6 结 论

为了解决非迭代解法精度较低，收敛性易受初始值的影响、不适用于大旋转角坐标转换的问题，本文提出联合两类解法来估计七参数。通过算例验证了联合解法的准确性与有效性，其中MatrixUQ 的迭代次数最少，转换后的坐标与目标坐标最接近。本文提出了一种不需迭代初始值而能应用于任意角度转换的联合估计七参数方法，但并没有将其与非线性最小二乘［9］等求解方法作对比分析，还有待进一步完善。

1 王之卓.摄影测量原理［M］.北京:测绘出版社.1990.(Wang Zhizhuo.Principle of photogrammetry［M］.Beijing:Surveying and Mapping Press，1990)

2 Arun K S，Huang T S and Blostein S D.Least-square fitting of two 3D point sets［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1987，9(5):698－700.

3 Horn B K P，Hilden H M nand Negahdaripour S.Closed-form solution of absolute orientation using orthonormal matrices［J］.Journal of the Optical Society of America A，1988，5(7):1 128－1 135.

4 Horn B K P.Closed-form solution of absolute orientation using unit quaternions［J］.Journal of the Optical Society of America A，1987，4(4):629－642.

5 Walker M W，Shao L and Volz R A.Estimating 3-D location parameters using dual number quaternions［J］.Image Understanding，1991，54(3):358－367.

6 曾文宪，陶本藻.三维坐标转换的非线性模型［J］.武汉大学学报(信息科学版)，2003，28(5):566－568.(Zeng Wenxian and Tao Benzao.Non-linear adjustment model of three-dimensional coordinate transformation［J］.Geomatics and Information Science of W uhan University，2003，28(5):566－568)

7 陈义，沈云中，刘大杰.适用于大旋转角的三维基准转换的一种简便模型［J］.武汉大学学报(信息科学版)，2004，29(12):1 101－1 105.(Chen Yi，Shen Yunzhong and Liu Dajie.A simplified model of three dimensional-datum transformation adapted to big rotation angle［J］.Geomatics and Information Science of Wuhan University，2004，29(12):1 101－1 105)

8 赵双明，等.基于四元数的三维空间相似变换解算［J］.武汉大学学报(信息科学版)，2009，34(10):1 214－1 217.(Zhao Shuangming，et al.Quaternion-based 3D similarity transformation algorithm［J］.Geomatics and Information Science of Wuhan University，2009，34(10):1 214－1 217)

9 陈宇，白征东.基于非线性最小二乘算法的空间坐标转换［J］.大地测量与地球动力学，2010，(2):129－132.(Chen Yu and Bai Zhengdong，An nonlinear least squares algorithm for spatial coordinate transformation［J］.Journal of Geodesy and Geodynamics，2010，(2):129－132)