几类埃尔米特插值及计算

王晓娥，苏岐芳

（台州学院 数学与信息工程学院，浙江 临海 317000）

几类埃尔米特插值及计算

王晓娥，苏岐芳＊

（台州学院 数学与信息工程学院，浙江 临海 317000）

讨论了两类埃尔米特插值多项式的构造方法，一类是带有一个导数的埃尔米特插值，另一类是带有多个导数的埃尔米特插值．分别从节点为几个的特殊情况，推广到具有任意多个节点的情况，推导出他们的插值多项式模型，给出了计算实例。

导数；节点；均差；埃尔米特插值

0 引言

在许多实际问题中，都用函数y=f（x）来表示具有某种内在规律的数量关系．但是，一般通过实验或观察得到的是部分数据，而不是全部数据．可利用给定的部分数据，通过插值法来构造一个既能反映函数f（x）的特性，又便于计算的简单函数P（x），即用P（x）近似f（x）．要求插值多项式P（x）与函数f（x）在插值节点上的函数值相等，也就保证了插值函数的连续性．但有些实际问题还需要插值的光滑度，即要求在节点处的导数值也相等，甚至高阶导数也相等，满足这种要求的插值多项式称为埃尔米特（Hermite）插值多项式［1-3］.埃尔米特插值法具有一定的实际应用，现代仿生学就是一个典型的实例.在设计交通工具的外形时，就是参照海豚标本上的已知点及若干已知点的导数做插值，在计算机上模拟海豚的外形设计飞机、汽车等的外形［4-9］.

定义函数f（x）关于点x0，x1的一阶均差为

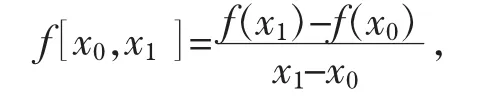
关于x0，x1，x2的二阶均差为

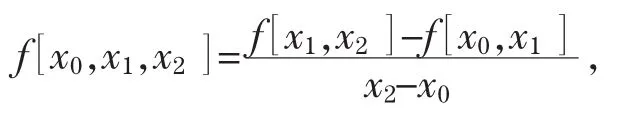
关于x0，x1，…，xk的k阶均差为

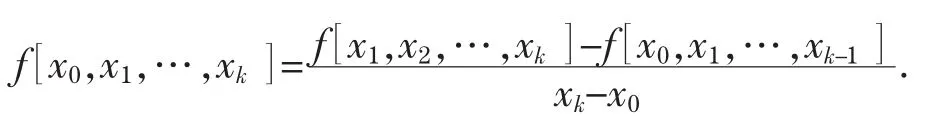
1 带有一个导数值的埃尔米特插值

1.1 三个节点的埃尔米特插值

要获得满足条件P（xi）=f（xi）（i=0，1，2）和P'（x1）=f'（x1）的插值多项式P（x），则由已知的条件，可确定它是次数不超过3的插值多项式.由于插值多项式通过点

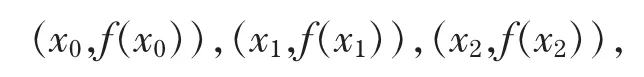
故其形式可设为

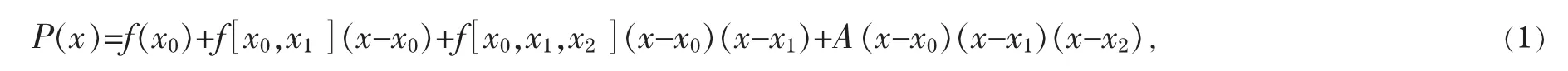
其中A为待定系数，由条件P'（x1）=f'（x1）确定.通过计算可得

1.2 四个节点的埃尔米特插值

要获得满足条件P（xi）=f（xi）（i=0，1，2，3）及P'（x1）=f'（x1）的插值多项式P（x），则由已知的条件，可确定它是次数不超过4的插值多项式．由于插值多项式通过点

1.3 节点为任意个的埃尔米特插值

要获得满足条件P（xi）=f（xi）（i=0，1，2，…n）及P'（x1）=f'（x1）的插值多项式P（x），则由已知的条件，可确定它是次数不超过n+1的插值多项式.由于插值多项式通过点

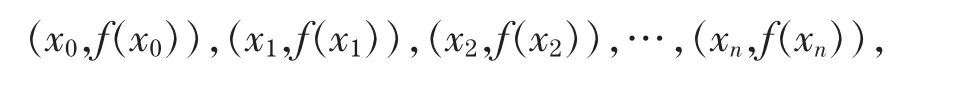
故可设其形式为

2 带有多个导数值的埃尔米特插值

2.1 带有两个导数值的埃尔米特插值

要获得满足条件P（xi）=f（xi）（i=0，1，2）及P'（x0）=f'（x0），P'（x1）=f'（x1）的插值多项式P（x），则由已知的条件，可确定它是次数不超过4的插值多项式．由于插值多项式通过点

故可设其形式为

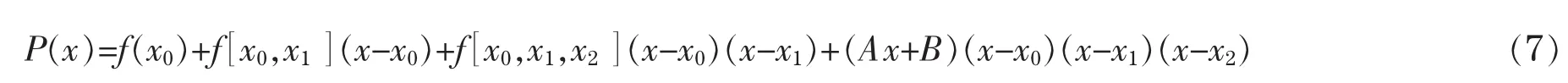
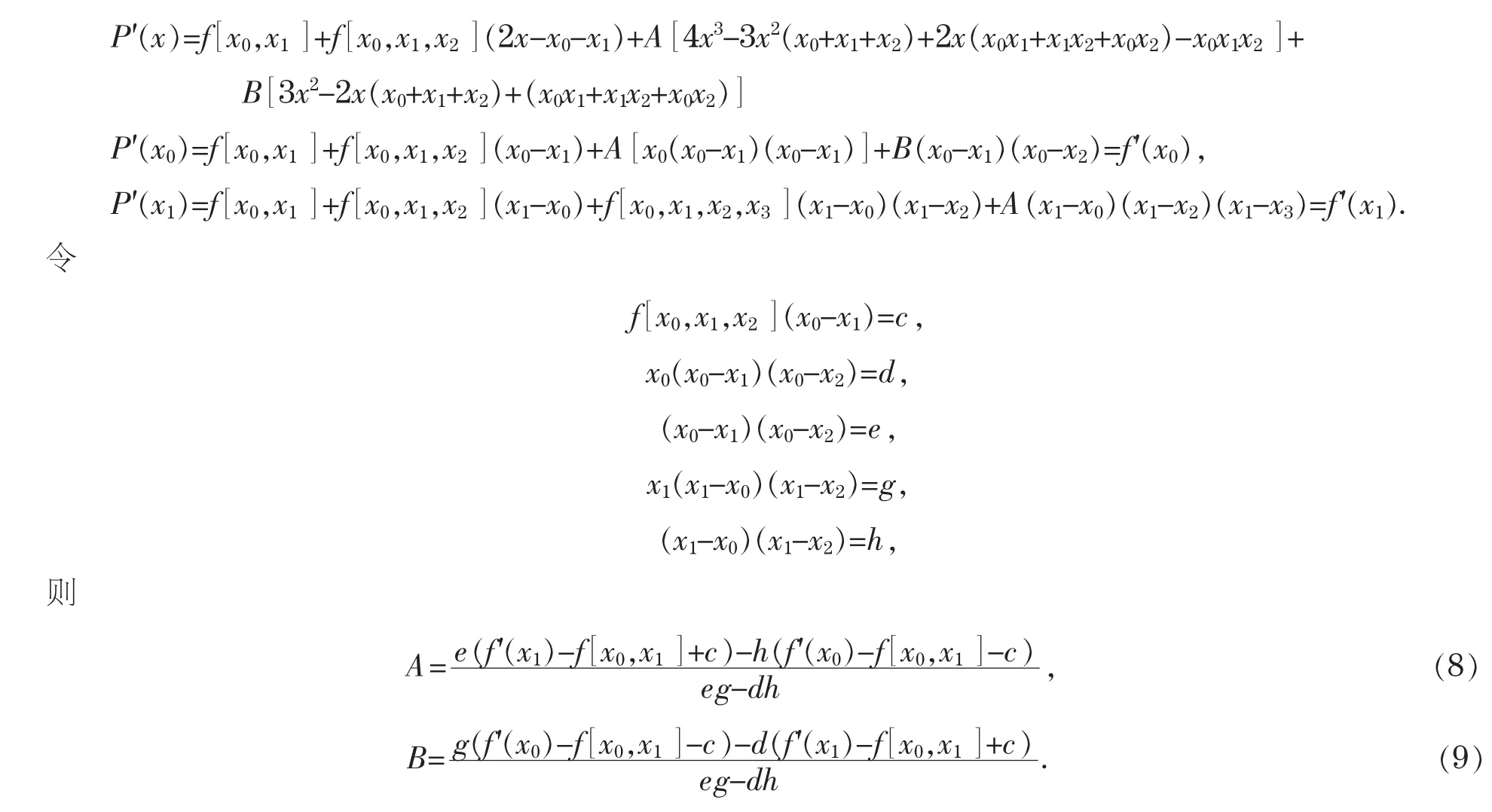
2.2 一般条件下的埃尔米特插值

要获得满足条件P（xi）=f（xi），（i=0，1，2）及P'（xj）=f'（xj），（j=0，1，2，…，m，m≤n）的插值多项式P（x），则由给定的条件，可确定它是次数不超过m+n+1的插值多项式.由于插值多项式通过点

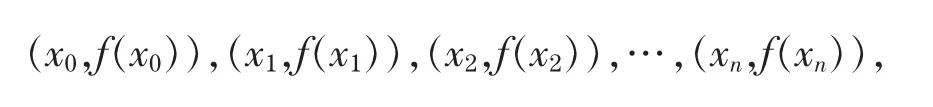
故可设其形式为

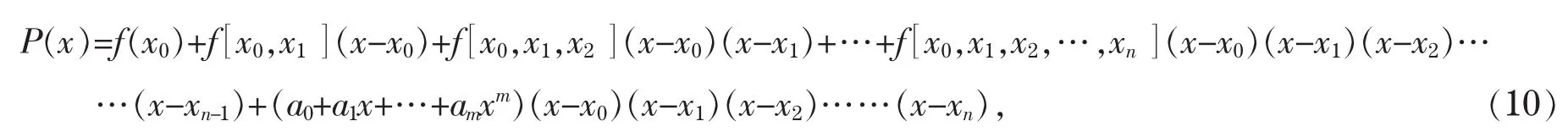
其中a0，a1，…，am为待定系数，可由条件确定.

3 埃尔米特插值法的应用

1.已知P（0）=0，P（1）=1，P（3）=9，P（5）=25，且f'（1）=P'（1），求满足条件的插值多项式P（x）．

由已知条件，可确定P（x）是次数不超过4的插值多项式，考虑到此多项式通过点

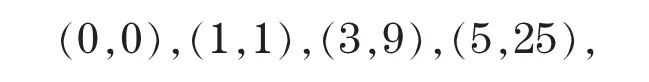
故可设

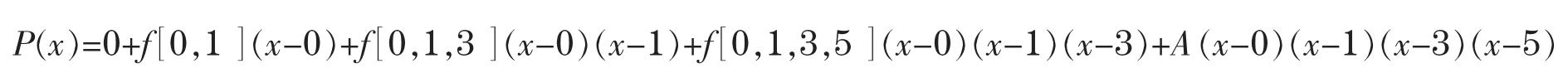
其中f［ 0，1 ］=0，f［ 0，1，3 ］=0，f［ 0，1，3，5 ］=0，A为待定系数，可由f'（1）=P'（1）=2确定．

代入公式（4）可得A=0，因此满足条件的插值多项式为P（x）=x2．

2.已知P（1）=2，P（2）=4，P（3）=16，且f'（1）=P'（1）=3，f'（2）=P'（2）=9，求满足条件的插值多项式P（x）．

由已知条件，可确定P（x）是次数不超过4的插值多项式，考虑到此多项式通过点

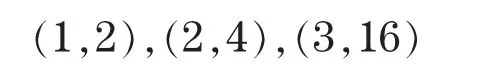
故可设

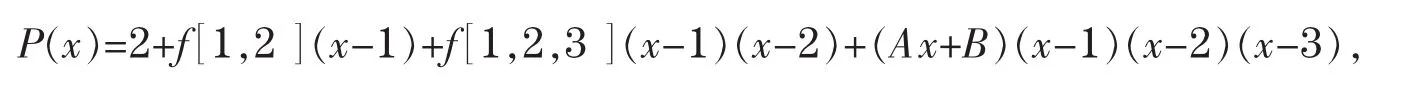
其中f［ 1，2 ］=2，f［ 1，2，3 ］=5，A，B为待定系数，可由f'（1）=P'（1）=3，f'（2）=P'（2）=9确定．

这里

因此，满足条件的插值多项式为

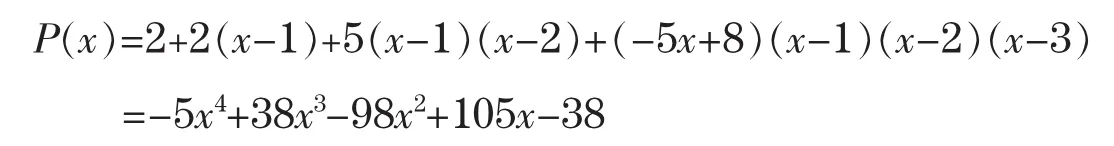
4 结束语

根据不同的条件，推导出了几类埃尔米特插值公式，可以直接应用到求解相关的实际问题中．在给定的条件下，可将已知数据直接代入到求得的公式中，方便快捷地求出插值多项式P（x），以便了解输入数据和输出数据之间的某种内在规律与关系．对于大规模数据，可设计算法的程序，利用计算机进行快速计算。

［1］李庆扬，王能超,易大义.数值分析［M］.5版.北京：清华大学出版社，2008．

［2］Richard L.Burden，J.Douglas Faires.数值分析 （NUMERICAL ANALYSIS）［M］.北京：高等教育出版社，2001.

［3］David Kincaid，Ward Cheney.数值分析 （Numerical Analysis）［M］.北京：机械工业出版社，2003.

［4］张洪波.插值法应用的实例分析［J］.华北科技学院学报，2010，7（3）:71-73.

［5］文畅平.埃尔米特插值函数的工程应用［J］.人民黄河，2006,28（4）:69-70.

［6］文畅平.埃尔米特插值函数在公路平面线形设计中的应用［J］.测绘科学，2007，32（3）:149-150.

［7］胡新源，沈以鸿，朱泽煌，等.应用埃尔米特插值作心电图基线漂移校正［J］.电子学报，1990（4）:35-41.

［8］王芳.牛顿插值法在中数中的应用［J］.浙江师范大学学报（自然科学版）,1994,17(4):67-73.

［9］李鹏,顾宏斌,高振兴.三次样条插值法在气动导数计算中的应用［J］.飞行力学,2008,26（2）:74-80.

Some Hermite Interpolations and Applications

WANG Xiao-e，SU Qi-fang＊

（School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China）

Two constructive methods about Hermite interpolation are discussed in this paper.One is Hermite interpolation with one derivative,and the other is Hermite interpolation with multiple derivatives.We first consider some special cases with some nodes,then extend to the general case.We derive some formulas of Hermite interpolation and give some examples.

derivative;node;difference quotient;Hermite interpolation

10.13853/j.cnki.issn.1672-3708.2014.06.001

（责任编辑：耿继祥）

2014-11-05；修改日期：2014-11-12

简介：苏岐芳（1964- ），女，黑龙江绥化人，副教授，硕土，主要从事计算数学研究。