二维变系数抛物型方程的一个高阶ADI差分格式
马小霞,颜晓琳,陈汝栋
(1.焦作大学 基础部,河南焦作 454003;2.天津工业大学 理学院,天津 300387)
二维变系数抛物型方程的一个高阶ADI差分格式
马小霞1,颜晓琳2,陈汝栋2
(1.焦作大学 基础部,河南焦作 454003;2.天津工业大学 理学院,天津 300387)
针对二维变系数抛物型方程,构造出了一个高精度、恒稳定的交替方向隐式(ADI)差分格式,格式的截断误差阶达O(τ2+h4).通过数值实验,验证了理论分析的正确性和差分格式的精确性与有效性.
抛物型方程;ADI格式;截断误差;恒稳定
抛物型方程在处理废料污染、渗透、驱动、海水入侵以及半导体等工程实际问题中有着广泛的应用,因此研究其高精度、高稳定和计算量较小的数值解法具有重要的意义.用有限差分方法研究这类问题的数值方法目前已做了许多工作[1-5].但这些工作大多是对常系数而言的.文献[4]中对二维变系数抛物型方程数值方法仅对系数依赖于一个变量的情况进行了研究,本文的研究是对系数依赖于两个变量的情形进行的.应用Taylor展开、算子方法[6]以及粘结系数法[7]得到了一个高精度(截断误差阶达O(τ2+h4))、恒稳定的ADI格式.格式的建立和稳定性分析都比文献 [4]简单得多,文末的数值实验证明了本文理论分析的正确性和所得格式的精确性与有效性.
1 差分格式的建立
考虑如下的二维变系数非齐次抛物型方程初边值问题

其中:0<c1≤a(x,y)≤c2;Γ为Ω的边界.
设τ=Δt=T/N为时间步长,h=Δx=Δy=1/M为空间步长,N、M均为正整数.表示在节点(jh, kh,nτ)处的网函数值,微分方程问题(1)—(3)的解函数为u(x,y,t),并记u(jh,kh,nτ)=u(j,k,n),由Taylor展开式


在(j,k,n+1)处考虑方程(1),根据粘结系数法[7]有

适当选取这些参数使得式(9)—式(11)成立.由于



即式(9)—式(11)的3个式子均成立,由式(8)、(14)、(16)和(17)得:


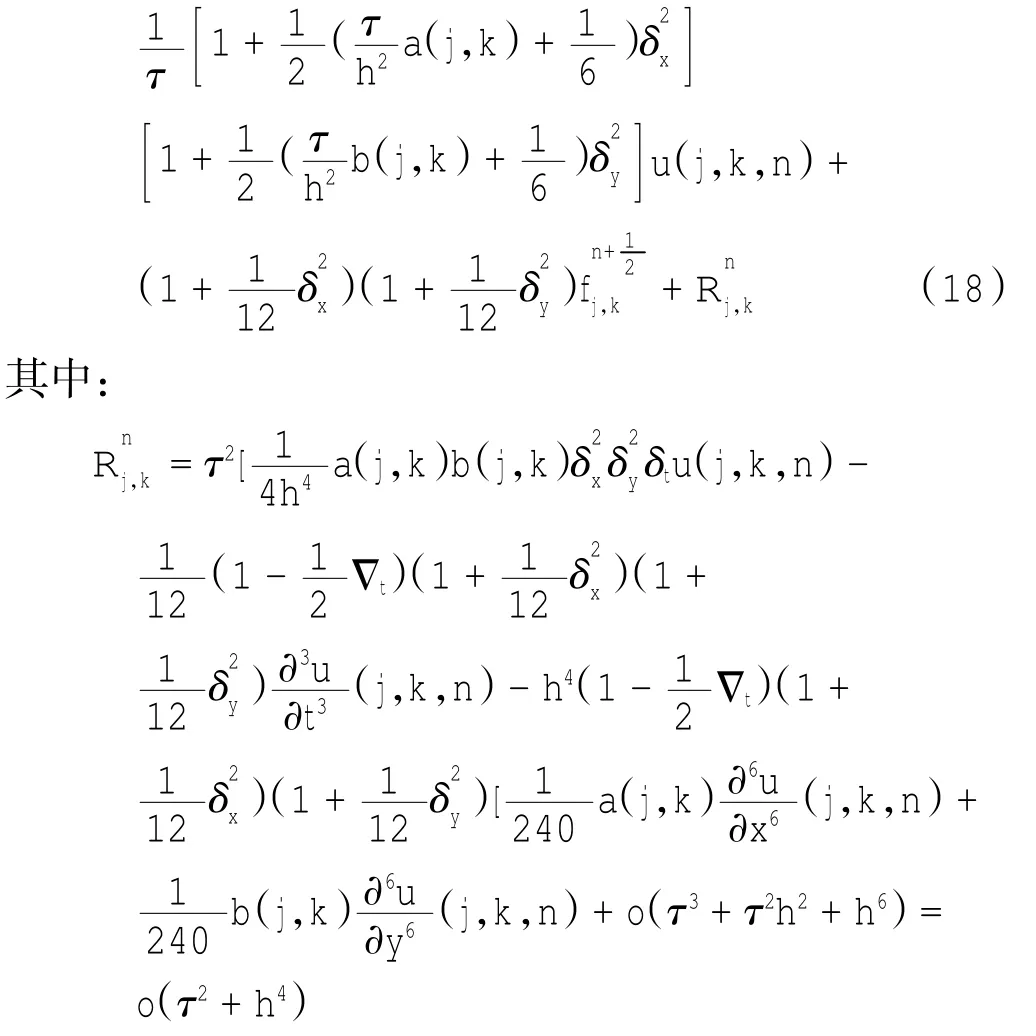




2 稳定性分析
为对格式(22)—(23)进行稳定性分析,可将过渡层变量消去,即得格式(19),故两格式有相同的截断误差和稳定性质.
因为差分格式关于初值稳定一定可以推出关于右端稳定,故只对齐次格式进行讨论,根据稳定性分析的Fourier方法[21],令

将上式代入格式(19)式的齐次形式中,经计算整理,并利用关系式



由s1的取值范围可知,

所以|G(s1,s2)|根据Von neumann条件知格式(19)也即格式(22)—(23)恒稳定.综合上节与本节的论述,并根据Lax的稳定性与收敛性等价原理可得:
定理 本文的ADI格式恒稳定且以o(τ2+h4)的收敛阶收敛.
3 数值实验
在区域D:{0≤x,y≤1,t≥0}上对初值边问题

用本文格式求数值解并与精确解u(x,y,t)=e-2tsin(x+y),相比较,取h=1/10,τ=rh2=r/100,r=1/2计算到n=200时的结果如表1所示.

表1 各种算法计算结果与精确解数值比较表Tab.1 Comparative table of algorithms results and exact numerical solutions
由表1结果看出,对所取的r,本文格式解与精确解均有很好的吻合,这与理论分析完全一致.
4 结束语
本文构造了二维变系数抛物型方程的ADI格式,数值例子表明,它具有易于计算(能三对角追赶法求解)、精度高(较现有格式)、无条件稳定等特点.本文构造出的格式可以推广到任意维变系数抛物型方程,对当前关于变系数抛物型方程差分格式的构造与研究有重要的理论和实践意义.
[1]DAI Weizhong,NASSAR Raja.A Second-order ADI scheme for three-dimensional parabolic differential equations[J].Numer Math,1964(6):428-453.
[2]DAI Weizhong,NASSAR Raja.Compact ADI method for solving parabolic differential equations[J].Numer Methods Partial Differential Eq,2002(18):129-142.
[3] 孙志忠,李雪玲.反应扩散方程的紧交替方向差分格式[J].计算数学,2005,19(2):209-224.
[4] 孙志忠,李雪玲.二维变系数反应扩散方程的紧交替方向差分格式[J].高等学校计算数学学报,2006,28(1):83-95.
[5] 马菊意,杨辉.二维抛物型方程的一个高精度PC格式[J].工程数学学报,2008,25(2):373-376.
[6]余德浩,汤华中.微分方程数值解法[M].北京:科学出版社,2003:102-174.
[7] 戴嘉尊,邱建贤.微分方程数值解法[M].南京:东南大学出版社,2003:91-93
[8]李立康,於崇华,朱政华.微分方程数值方法[M].上海:复旦大学出版社,1999:208-213.
A high accuracy ADI difference scheme for solving two-dimension variable coefficients parabolic equation
MA Xiao-xia1,YAN Xiao-lin2,CHEN Ru-dong2
(1.Department of Basic Course,Jiaozuo University,Jiaozuo 454003,China;2.School of Science,Tianjin Polytechnic University,Tianjin 300387,China)
A high accuracy alternation direction implicit scheme(ADI)for solving the two-dimensional parabolic equations is presented,and the scheme is absolutely stable and the truncation error is O(τ2+h4).The experiments show the scheme is effective and advantage,and the theory is right by a numerical example.
parabolic equation;ADI difference scheme;truncation error;absolutely stable
O241.82
A
1671-024X(2014)01-0077-04
2013-05-31
国家自然科学基金(11071279);河南省教育厅自然科学基础研究基金(2008B110016)
马小霞(1969—),女,硕士,讲师.
陈汝栋(1956—),男,教授,硕士生导师.E-mail:chenrd@tjpu.edu.cn

