油墨预设LS-SVM模型研究

王毅, 刘凯, 张海燕, 曹从军

(1.西安理工大学 印刷包装工程学院，陕西 西安 710048;2.西安理工大学 机械与精密仪器工程学院，陕西 西安 710048)

在工信部发布的《产业关键共性技术发展指南》 中[1]，对印刷行业提出重点突破“高端、智能化印刷机墨色控制系统技术”，以油墨预设为代表的关键技术是近年突破解决印刷墨色控制的热点研究方向。

油墨预设的核心思想是将印前版面的数字化图文信息通过一定的数学方法，自动转换为与之匹配的印刷机输墨系统墨键开度信息，通过适配印刷机在不同生产环境下的供墨量修正方案，进而达到油墨自动预设的目的。油墨预设的关键技术是建立墨区图文面积覆盖率和实际印刷时各墨区的墨键开度值之间的非线性关系[2-3]。

最小二乘支持向量机(LS-SVM )[4-6]较好地解决了小样本、非线性、高维数和局部极值等问题，是解决胶印输墨系统中的输入墨量和经过预设控制后的输出墨量之间非线性关系、实现准确预设的较好研究方法。

1 LS-SVM算法

假设给定m个样本点{(x1,y1),(x2,y2),…,(xm,ym)},其中xi∈Rn是n维输入量，yi∈Rm是m维输出量，yi=f(xi),i=1,2,…,m。f(x)为待估计的未知函数。做非线性映射φ:Rk→H，在高维特征空间中构造最优决策函数f(x)：

y=f(x)=ωTφ(x)+bω∈Rh,b∈R

(1)

式中,h为高维特征空间维数，ω为空间H中的权向量，b为偏置量。

根据问题求解目标和结构风险最小化的原则，上式需满足如下条件：

(2)

最小二乘支持向量机的最优化问题可转化为：

(3)

式中,γ为惩罚系数，γ∈R，ei∈R为误差松弛因子变量。

由于ω可能是高维或无限维，致使计算非常困难，因此转换到其对偶空间中，用Lagrange乘子法求解，定义Lagrange函数：

(4)

其中αi∈R为Lagrange乘子(i=1,2,…,m)。

根据KKT条件，分别求L对式中的ω、b、αi和ei的偏导数并令偏导数等于0，可得：

(5)

消去ω和ei可得矩阵方程：

(6)

式中:

y=[y1,y2,…,ym]T

I=[1,1,…,1]T

α=[α1,α2,…,αm]T

[Ωi,j]=[Κ(xi,xj)]

其中[Ωi,j]是一个方阵，称之为核矩阵，Κ为定义的核函数。

由Mercer条件可得：

Ωi,j=φ(xi,xj)=Κ(xi,xj)i,j=1,2,…,m

(7)

最后得到最小二乘支持向量机的函数模型为：

(8)

最小二乘支持向量机中所有的训练样本都认为是支持向量，最小二乘支持向量机仅需要确定核函数的形状参数和正规则化参数，而不需要选取不敏感损失函数值，从而方便计算。

2 基于LS-SVM的油墨预设控制模型

油墨预设是根据印版图文的分布情况来确定胶印机对应墨区的墨量，某一墨区的给墨量又是通过胶印机相应墨区的墨键系统来控制[7-8]。但在实际印刷中，串墨辊有特殊的运动状态，如图1所示，串墨辊在周向转动的同时还轴向串动，通过摩擦力将油墨在周向和轴向两个方向打匀。

图1 串墨辊运动示意图

由于串墨辊和匀墨辊的混合运动，一方面使墨区油墨更均匀地分布，但另一方面也使某一墨区初始预设的墨量受到相邻墨区墨量串动的影响，使初始预设墨键开度与最终到达承印物表面的墨量之间变为更复杂的非线性关系。因此考虑匀墨系统串墨的影响，基于最小二乘支持向量机建立墨键开度与分墨区图文网点覆盖率之间的非线性模型，才能解决油墨预设精度问题。

假设胶印机给定的墨区数为N，其中xi(i=1,2,…,n)表示印品分墨区的图文网点面积覆盖率，xi可由印前样张图文处理后的1-bit TIFF文件得到[9]，并把它作为油墨预设模型的输入，yi(i=1,2,…,n)表示对应的胶印机墨区墨键开度的大小，作为油墨预设模型的输出。实际印刷中，由于串墨辊轴向串动的原因，串动量会影响相邻墨区墨量的变化，影响墨区墨量的范围取决于轴向串动量的大小，一般来说相邻两个墨区的影响程度相对较大。因此，本文基于每一个输出yi，采用xi-2，xi-1，xi，xi+1，xi+25个墨区的图文网点覆盖率与之对应并建立映射关系，这样就建立起油墨预设控制模型，如图2所示。

图2 油墨预设控制输入输出模型

建立基于最小二乘支持向量机的油墨预设控制模型的具体流程为：

1)确定油墨预设变化的各个自变量属性；

2)确定胶印油墨预设的训练样本和预测样本，即印品样张的网点面积覆盖率和对应墨区的墨键开度值；

3)确定最小二乘支持向量机选用算法对参数的寻优结果；

4)训练样本，根据训练得到的最小二乘支持向量机模型，进行预测，得到墨键开度预设值；

5)对胶印油墨预设结果进行检验，并与实际结果进行分析对比。

3 仿真实验

实验以典型的海德堡SM74胶印机为例，四色印刷单元，输墨系统有23个墨区，预先选用测试样张(见图3)印制后获得的基本数据作为训练样本数据。

图3测试样张示例

为了得到更好的预测效果，选用了和声搜索算法优化得到的两个模型参数γ和δ最优值，(文献[10]中介绍了和声搜索算法的具体步骤和其优点，在此不做具体介绍。)通过最小二乘支持向量机模型对预先印制测试样张数据进行训练，样张各墨区对应的网点覆盖率为从印前图文处理后的1-bit TIFF文件直接获得的结果，得到Lagrange 乘子α为1×23的矩阵, 核函数Κ为23×23的矩阵。

以测试样张青色分色数据为例，测试样张青色机组墨分墨区网点覆盖率如图4所示，印刷过程中实际油墨预设值如图5所示，最小二乘支持向量机油墨预设模型预设值如图6所示，测试样张分墨区预设对比结果如图7所示。

图4 测试样张分墨区网点覆盖率

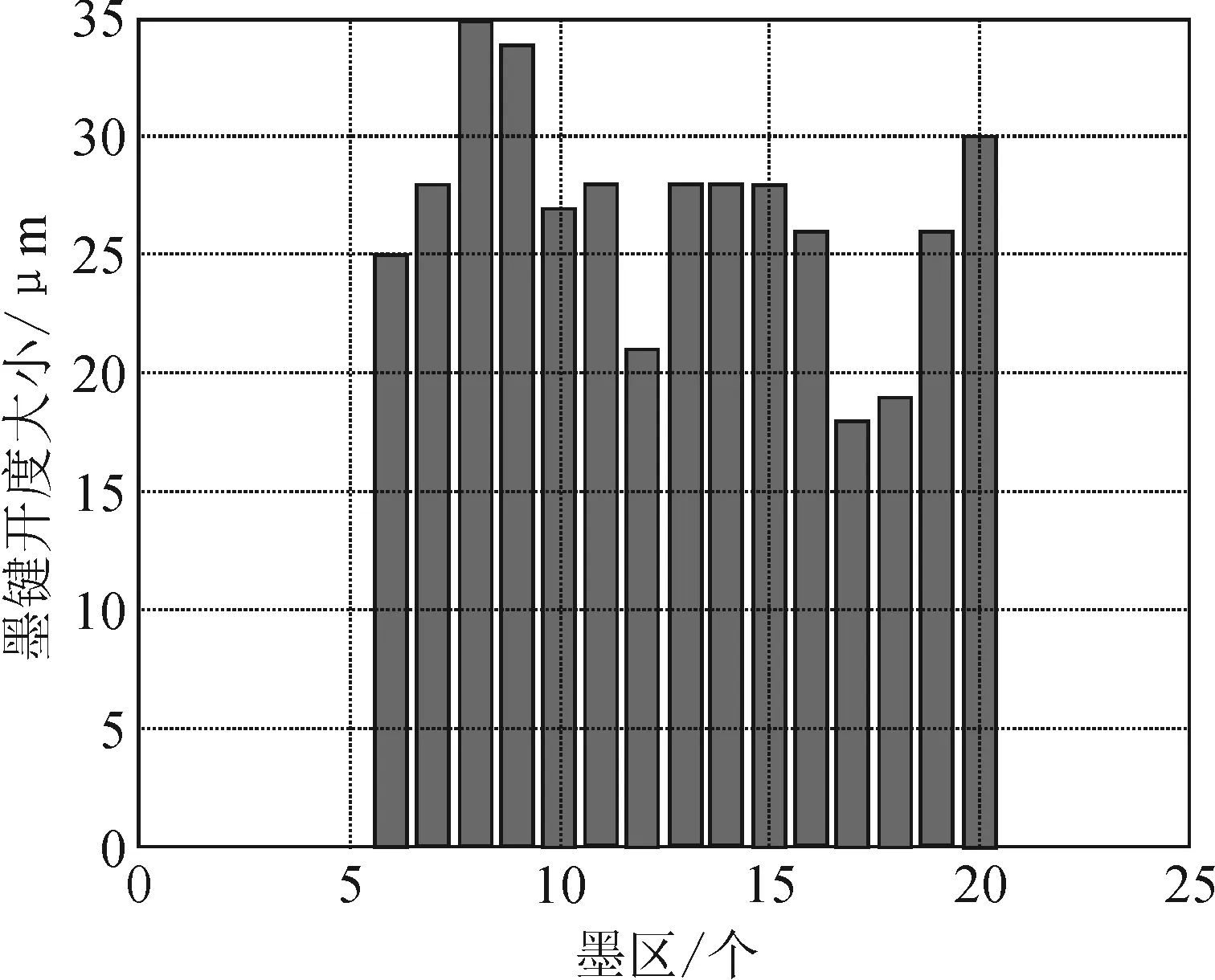
图5 测试样张分墨区实际油墨预设值

图6 最小二乘支持向量机油墨预设模型预设值

图7 预设结果对比

采用以下三个检验指标进行模型精度检验[11]。

1)误差均方根值：

(9)

2)误差最大绝对值：

(10)

其中AE为验证误差绝对值。

3)误差平均绝对值：

(11)

仿真性能检验结果如下：

σ=1.574 2

maxAE=4.972 4

AE=2.478 3

从上述检验结果可以看出，LS-SVM模型在油墨预设控制过程中预测精度高，学习能力强，仿真结果基本准确反映了墨键开度的真实值。

4 结 论

本文针对胶印印刷过程中受串墨辊串动影响带来的油墨预设精度问题，提出了利用最小二乘支持向量机解决印品墨区图文网点覆盖率与墨键开度之间的非线性问题，建立了基于LS-SVM的多元映射油墨预设模型。结果显示模型预测精度高，通过三个误差检验，说明本模型比较准确地反映了实际生产油墨预设的真实情况，说明该油墨预设模型具有更高的预测精度和稳定性。

参考文献：

[1] 中华人民共和国工业和信息化部. 产业关键共性技术发展指南(2011)[Z], 2011.

[2] 余节约. 胶印油墨预设机制与技术研究[D]. 南京: 南京林业大学, 2012.

Yu Jieyue. Study on the mechanism and technology of offset ink preset[D]. Nanjing: Nanjing Forestry University, 2012.

[3] Linus Lehnberg. Ink key presetting in offset printing press using digital images of the plates[D]. Sweden: Department of Science and Technology，Linkoping University, 2012.

[4] 余节约,林剑,管力明,等.基于最小二乘支持向量机的平版印刷油墨预置模型[C]//29届中国控制会议，2010:3103-3106.

Yu Jieyue, Lin Jian, Guan Liming, et al. Model of ink preset for offset printing based on LS-SVM [C]//Proceedings of the 29th Chinese control conference, 2010:3103-3106.

[5] 王定成．支持向量机建模预测与控制[M]．北京:气象出版社，2009.

[6] 杜鹃．基于支持向量机的非线性预测控制研究[D]．杭州:浙江大学，2006.

Du Juan.Research on nonlinear predictive control based on support vector machine [D]．Hangzhou:Zhejiang University,2006.

[7] Chu Chialin, Amit Sharma. Validating a modelbased ink key presetting system[C]//Technical association of the graphic arts 50th annual technical conference, 2008: 335-370.

[8] Wang Cinyin，Li Chao，Dai Qinling．A CIP3 ink presetting model for offset printing presses [C]//2010 International conference on computer science and software engineering,2010:402-405.

[9] Linus Lehnberg. Ink key presetting in offset printing presses using digital images of the plates[D]. Department of Science and Technology, Sweden: Link Pings University, 2002.

[10] 林剑，许力. 基于全局和声搜索优化的平版印刷油墨预设[J].仪器仪表学报, 2010, 31(10)：2248-2253.

Lin Jian, Xu Li. Global harmony search optimization based ink preset for offset printing[J]. Chinese Journal of Scientific Instrument, 2010, 31(10)：2248-2253.

[11] 刘美, 陈政石, 孙宗海. 基于小波-最小二乘支持向量机的熔融指数预测[J]. 计算机仿真, 2009, 26(10):162-165.

Liu Mei, Chen Zhengshi, Sun Zonghai. Prediction of melt index based on wavelet and LS-SVM[J]. Computer Simulation, 2009, 26(10):162-165.