基于激光三角法的石油管螺纹轮廓测量误差分析及处理

于殿泓，张路，李琳

(西安理工大学 机械与精密仪器工程学院，陕西 西安 710048)

在石油工业钻井和采油作业中，为保证油井管的结构完整性、密封完整性和可靠的互换性[1]，需要对出厂石油管的管螺纹进行严格检验。本文的研究内容建立在非接触式石油管螺纹测量系统基础上。该系统采用了经典的直射式激光三角法测量[2-4]，通过扫描管螺纹轮廓形状，从而计算出管螺纹的各个参数[5-6]，通过衡量这些参数来判断该管螺纹是否合格。而实际系统中，存在不可避免的影响因素。其中管螺纹的表面光洁度会对扫描光斑的漫反射造成影响，但是最主要的是系统的结构因素，由于螺纹沿轴剖面轮廓线的法线方向与系统的扫描光线不共线，这就会使得接收光斑质心产生偏移，从而使扫描结果存在偏差。所以要处理和分析这方面的问题才能得到理想的测量结果。

1 石油管螺纹测量方法

以非接触式激光测量为前提[7]，测量系统原理图如图1所示。以步进电机驱动丝杆实现激光传感器的光束在螺纹轮廓线上的扫描运动，轮廓线的Y向坐标值由激光传感器获取[8-9]，X向的坐标值由丝杠和相配合的圆编码器获取，将所测量出的一系列坐标数据进行拟合，便可得出被测螺纹的轮廓线，进而实现对相关螺纹参数的评定。

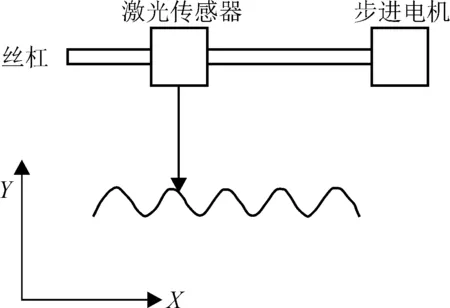
图1 测量系统原理图

典型的激光三角法测距光路如图2所示。系统主要由激光源、会聚透镜、接收透镜、光敏元件(主要是PSD[10]或CCD[11])等组成。由激光源发出一束激光，经过会聚透镜在被测表面汇聚成一个微小光点，当光点在被测表面位置发生变化时，光电检测器件就可以检测到漫反射所形成光斑位置的变化。该散射光斑的中心位置由传感器与被测物体表面之间的距离决定。由于光斑中心位置的变化可以引起光电检测器件输出电信号的变化，通过分析计算处理光电检测器件输出的电信号，就可得知传感器与被测表面相对位置变化的信息。

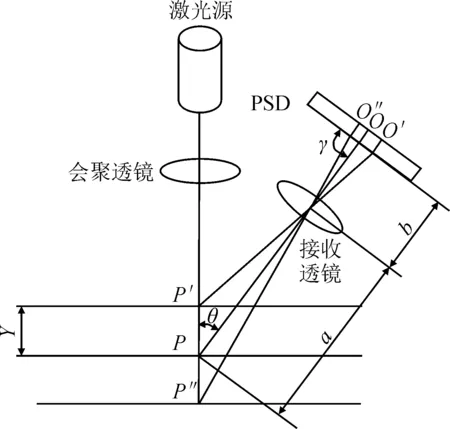
图2 激光三角法测量原理

被测物体表面位于参考面P时，光斑在PSD或CCD中心位置O处成像，当被测面相对于参考面位移发生变化时，PSD或CCD上接收到的光斑位移为x，x=OO′，y与x就会存在以下关系：

(1)

对于该关系式，当被测表面位于参考面的下方时取减号，位于参考面的上方时取加号。

2 产生误差的因素

由于光学部件以及机构部件在制造过程中不可避免会存在误差，有些误差可以由改善生产工艺或使用方式等措施进行消除，例如被测螺纹表面光洁度如果过大，会产生较强的镜面反射，如果过小，会影响原光点的均匀性[12]，使光电检测器输出不稳定，这就要通过改变激光器的功率或使用偏振片削光来减少光强变化对测量的影响。

当被测螺纹表面光洁度处于0.32至2.5这个范围时可不考虑此项误差[13]。

本文主要针对螺纹牙型角这样一个特定的被测参数对测量结果的误差进行研究与分析，这种误差无法采用一般手段进行消除，所以就要通过理论分析和实验相结合来研究出一套补偿方案。本系统中采用的是激光三角法测量中的直射式测量，要求发射光束始终与被测表面法线方向一致。而该方法的发射光束方向与石油管的轴向垂直，误差产生示意图如图3所示。

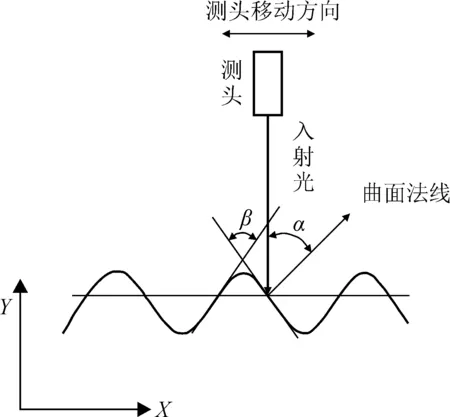
图3 误差产生示意图

由于螺纹牙型角度的存在，就相当于入射光束入射到了一个有倾角的斜面。入射光束与被测螺纹表面法线夹角即为倾角α，倾角α与螺纹牙型角β的关系为：

α=90°-β/2

(2)

这会导致入射光点产生的散射光空间分布相对于入射光束与法线方向一致时发生变化，使得光电接收面上单位时间接收的光能量产生变化，从而光斑质心相对于其几何中心出现偏移，由于光电检测元件(PSD或CCD)检测的是投射到其上的光斑的光能质心的位置，而不是几何中心位置，就会使测量的结果与三角法测量原理公式的计算结果有偏差量[14]。

3 误差补偿实验设计

对于所测平面倾角对测量结果所产生的误差，本文根据圆(球)的弓高-弦长的严格对应关系，设计了以万能工具显微镜为实验平台，用标准球对激光传感器按规划路径进行标定测量，将测量数据进行拟合处理得出补偿规律。

本系统中所用传感器是基恩士公司的IL-S065激光位移传感器，该传感器对于特定的被测表面(倾角一定)，能够表现出很好的重复性，因此可对不同倾角的被测面进行测量得到测量值并与理想值作比较得出误差规律，从而对测量结果进行修正。这种方法可以显著地提高测量精度。

3.1 实验设计

实验装置包括万能工具显微镜、激光位移传感器(型号：基恩士IL-S065)、标准钢柱(R柱= 9 mm)、标准钢球(R球= 13 mm)等组成。

将激光位移传感器固定到万能工具显微镜的立柱上，以钢球或钢柱作为扫描对象，进行多次扫描实验。对钢柱或钢球径向进行的扫描就相当于扫描一个倾角从0°到90°变化的被测面，从而通过一次扫描就可以得到当被测表面倾角变化时所产生误差的大小。

实验设计原理图如图4所示。图5为实验设计的实物图。

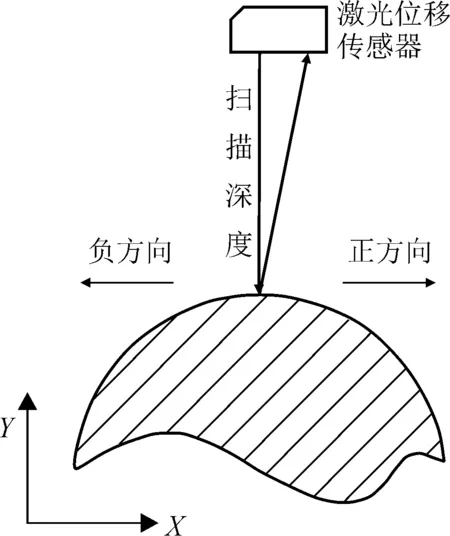
图4 实验设计原理图

图5 现场实验

3.2 实验实现

将激光位移传感器固定在万能工具显微镜的立柱上，调整立柱的高度，确保整个扫描过程中的扫描深度在该传感器的量程范围(-10 mm至10 mm)。将钢柱或钢球置放于万能工具显微镜的工作台上，由于激光位移传感器是固定的，所以通过工作台在X方向上的移动来完成扫描过程，相当于扫描一个倾角从0°到90°变化的平面。以钢球或钢柱轮廓弧顶为原点，在X方向上每进给0.5 mm，在传感器上读取一个值。完成一次扫描，就可以通过得到的位移数据来拟合出扫描面的轮廓，其中钢球的极限进给量为-11.5 mm至11.5 mm，钢柱的极限进给量为-8 mm至8 mm。

对钢柱和钢球分别进行三次正方向扫描和三次负方向的扫描，然后对扫描结果进行统计并计算。

3.3 实验数据分析

误差分析示意图如图6所示。

图6 误差分析示意图

传感器光斑投射在钢柱或钢球最高点A1点时，激光传感器的读数值为y1。当光斑在X方向进给Δx时，相当于其扫描表面倾角为α：

(3)

此时光斑位于A2点，激光传感器的读数值为y2。由此可知，在测量进给为Δx时，激光传感器的两次读数的差值h1为：

h1=|y2-y1|

(4)

实际上，该差值h1即为实际测量中相应圆弧的弓高。而理论上该段圆弧的弓高h2为：

(5)

由此可知，当被测表面倾角为α时，激光传感器产生的测量误差δ为：

δ=h2-h1

(6)

3.4 实验结果

根据每一次扫描结果可以计算出相应倾角所对应的误差，采用三次多项式拟合法将所得到的数据点进行拟合。其中两组数据拟合结果如图7、图8所示。

图7 倾角-误差关系图(钢柱)

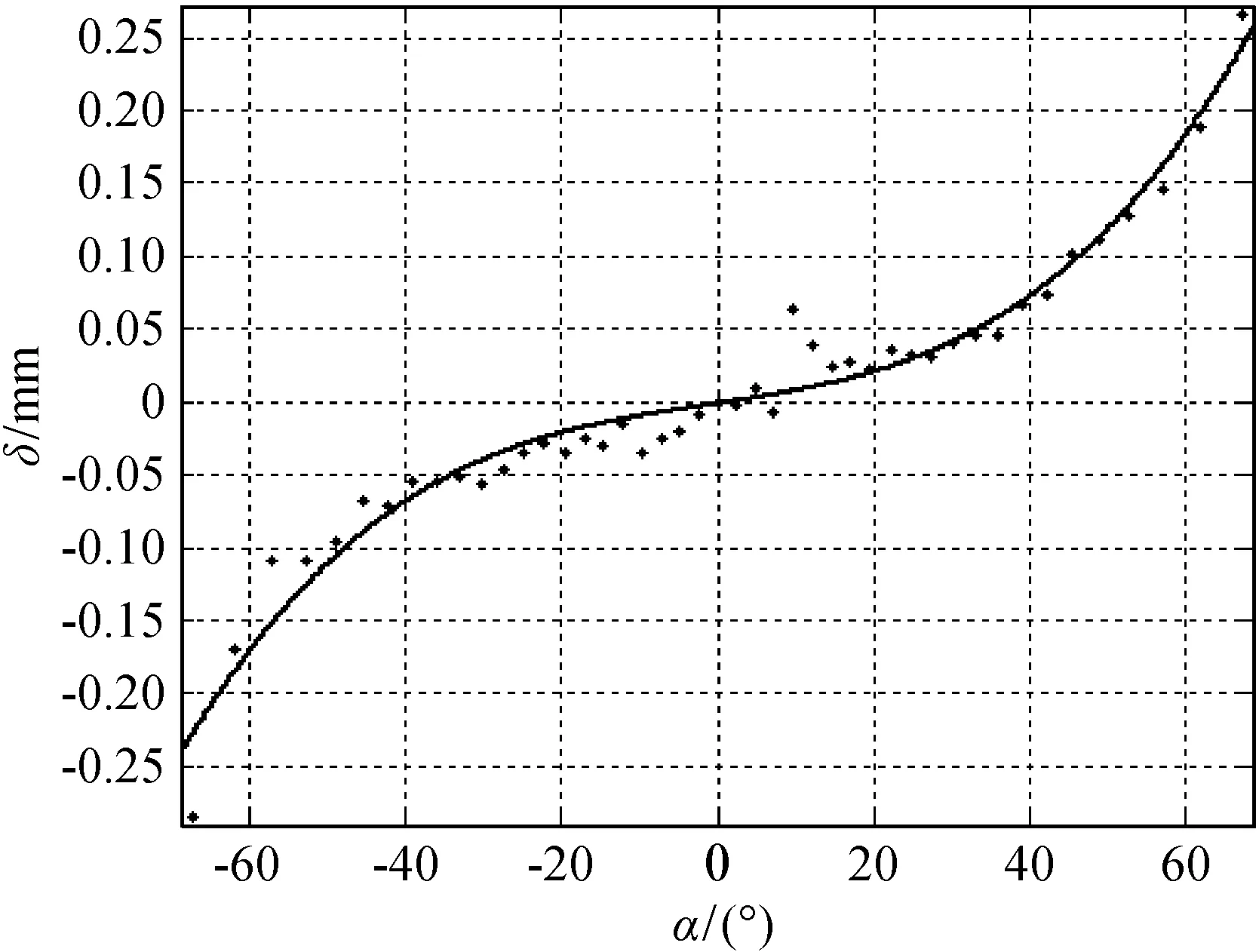
图8 倾角-误差关系图(钢球)

由图7和图8可见，不管采用何种实验样件(钢柱或钢球)，倾角-误差关系曲线的变化趋势是一致的，但样件不同，数值有所差别。主要原因在于：所研究的激光位移传感器的光斑为椭圆光斑，而非圆光斑，这样，在对钢球样件扫描过程中，通过调整工作平台X和Y方向上位置，找出激光位移传感器扫描钢球的最大读数，此时光斑位置视为钢球顶点，这时不论在X还是Y方向上移动平台，光斑都始终沿着钢球的圆心截面。但是对于钢柱而言，找到其最高点之前应该保证钢柱轴线方向、工作平台X位移方向以及光斑长轴方向平行，如果不平行则会引入使曲线变化趋势加大的误差。在实验中我们采用各种辅助工具来尽可能地保证这三者的平行，但是还是不可能保证完全平行，因此可以推断扫描到同一倾角时钢柱对应的误差会稍大。通过对比图7与图8发现，在倾角为40°时钢球对应的误差只有0.07 mm左右，而钢柱对应的误差却达到了0.09 mm，这一差别就是由上述原因造成的，理论而言，钢球样件的扫描结果更具有参考价值。将所有拟合好的曲线都放在一张图上的效果如图9所示。

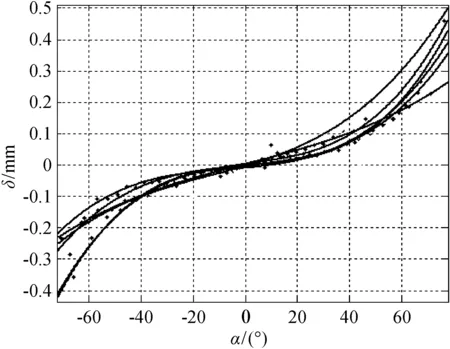
图9 误差-倾角关系图

将拟合好的所有曲线分别离散化，他们的横坐标范围为(-65°～65°)，对钢球样件实验得出的5条曲线同一横坐标所对应的5个纵坐标值求均值，最后以统一后的横坐标为横坐标以所求均值为纵坐标对其再次进行拟合就得到了这5条曲线的等效曲线，如图10所示。

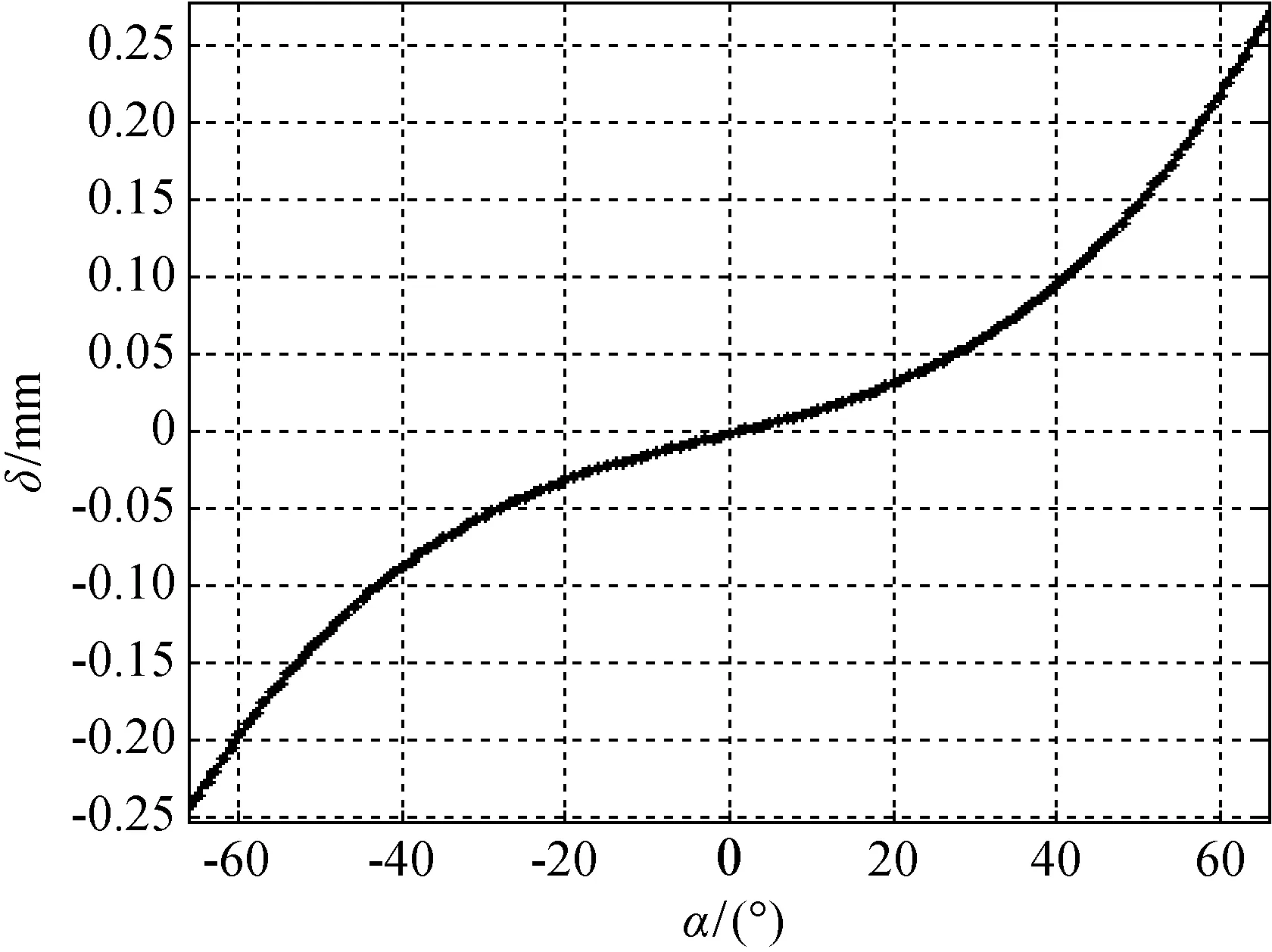
图10 误差补偿曲线

这就是最终的误差补偿曲线，横坐标是倾角大小，当横坐标值为零时表示被扫描平面法线方向与扫描光线方向共线，其误差为零。随着被扫描面的逐渐变大，测量系统的误差值也就随之变大。

4 误差补偿方案

根据等效曲线所显示出的误差与倾角关系图，在实际测量过程中就可以针对不同斜面的倾角来推算出所对应的误差并加以补偿，这对非接触式螺纹测量系统应用的广泛程度是具有实际意义的。

在扫描牙型角为60°的管螺纹时，相当于被测表面倾角为60°，可以通过查询“误差补偿曲线”就可以对扫描得到的螺纹左轮廓数据和右轮廓数据分别进行补偿。这样，在计算螺纹螺距、牙高等其他参数时所得的结果就可以更为精确。

由本次实验结果分析可以得出：由被测表面倾角产生的误差随倾角的增大而增大，偏差的正负和倾角α的正负相同，这与文献[15]中所做的理论分析计算得出的结论相一致。所以根据实验得出的补偿参数可以进一步提高非接触式螺纹测量系统的测量精度。

5 结 语

本文针对非接触式螺纹参数测量方案所产生的误差进行了深入分析，针对螺纹轮廓面法线方向与激光入射方向存在夹角的问题，通过搭建实验对测量结果进行修正，计算出相应倾角时对应的具体误差，由此可以在实际应用过程中进行相应补偿，使该系统测量精度进一步提高。

参考文献：

[1] 陈守俊. 油套管螺纹联接力学行为及粘扣失效过程研究[D]. 广州:华东理工大学, 2011: 1-11.

Chen Shoujun. Research on the mechanical behavior and gluing failure process in oil pipe threaded connection[D]. Guangzhou:East China University of Science and Technology, 2011: 1-11.

[2] Bala M, Wei Ren, Dennis E, et al. Performance evaluation experiments on a laser spot triangulation probe[J]. Measurement, 2012, 45(3): 333-343.

[3] Toru O, Hajime N, Masahiro T, et al. Development of a micro-optical distance sensor[J]. Sensors and Actuators A: Physical, 2003, 102(3): 261-267.

[4] Wang Xiaojia, Gao Jun, Wang Lei. Survey on the laser triangulation[J]. Chinese Journal of Scientific Instrument, 2004, 24(4): 601-604.

[5] 何富君, 张瑞杰, 兰爽, 等. 圆锥外螺纹的线阵CCD非接触检测法[J]. 哈尔滨工业大学学报, 2008, 40(7): 1169-1172.

He Fujun, Zhang Ruijie, Lan Shuang, et al. Measurementsof non-contact external tapered thread based on linear array CCD[J]. Journal of Harbin Institute of Technology, 2008, 40(7): 1169-1172.

[6] 周强, 张慧慧. 基于动态线性回归的一阶导数分段法在螺纹检测数据处理中的应用[J]. 北京工业大学学报, 2000, 26(4): 20-23.

Zhou Qiang, Zhang Huihui. Application of first differential grouping method based on the dynamic linear regression in thread testing[J]. Journal of Beijing Polytechnic University, 2000, 26(4): 20-23.

[7] 徐爱群, 项占琴, 陈子辰. 非接触式自动螺纹检测仪的研制[J]. 浙江大学学报:工学版, 2005, 39(8): 1180-1183.

Xu Aiqun, Xiang Zhanqin, Chen Zichen. Development of non-contact automatic thread measuring instrument[J]. Journal of Zhejiang University(Engineering Science), 2005, 39(8): 1180-1183.

[8] Lombardo V, Marzulli T, Pappaletter C, et al. A time-of-scan laser triangulation technique for distance measurements[J]. Optics and Lasers in Engineering, 2003, 39(2): 247-254.

[9] 吕东方, 振良, 袁峰. 光针轮廓扫描技术测量内螺纹曲面[J]. 光学精密工程, 2007, 15(2): 186-191.

Lü Dongfang, Zhen Liang, Yuan Feng. Measurement of inside screw curve surface by laser probe[J]. Optics and Precision Engineering, 2007, 15(2): 186-191.

[10] 丁硕，杨友林，巫庆辉.基于PSD的微位移传感器建模的实现方法[J].电子设计工程, 2012，20(11): 8-10.

Ding Shuo, Yang Youlin, Wu Qinghui. Realization of PSD based micro-displacement sensor modeling[J]. Electrical Design Engineering, 2012，20(11): 8-10.

[11] Shiou Fangjung, Liu Minxin. Development of a novel scattered triangulation laser probe with six linear charge-coupled devices (CCDs)[J]. Optics and Lasers in Engineering, 2009, 47(1): 7-18.

[12] Shen Lei, Li Dinggen, Luo Feng. A study on laser speckle correlation method applied in triangulation displacement measurement[J]. Optik, 2013, 124(20): 4544-4548.

[13] 徐春玉, 解则晓, 冯国馨, 等.被测表面特征对激光测头特性影响[J]. 天津大学学报, 2001, 34(6): 796-799.

Xu Chunyu, Xie Zexiao, Feng Guoxin, et al. Study on influence of surface properties on characteristics of laser triangulation probe[J]. Journal of Tianjin University, 2001, 34(6): 796-799.

[14] 鞠华. 逆向工程中自由曲面的数据处理与误差补偿研究[D]. 杭州: 浙江大学, 2003: 62-65.

Ju Hua. Research on data processing and error correction for freeform surface of reverse engineering[D]. Hangzhou, Zhejiang University, 2003: 62-65.

[15] 庄葆华, 王少清, 张吉华, 等.高精度激光三角法位移测量被测表面倾斜影响研究[J].计量技术, 1996, (2): 2-4.

Zhuang Baohua, Wang Shaoqing, Zhang Jihua, et al. Study on influence of the measured surface inclination of high precision laser triangulation[J]. Measurement Technique, 1996, (2): 2-4.