板壳结构加强筋仿叶脉分布声辐射优化研究
史冬岩, 颜凤眠, 韩家山, 石先杰
(哈尔滨工程大学机电工程学院, 黑龙江 哈尔滨 150001)
引 言
板壳结构有着优异的传力性能,能够形成刚度大、承载强的承重结构,由于其易于加工和轻量化的优点被广泛应用于航空航天、汽车制造和船舶工业等领域。但是板壳结构一般都具有刚度较小、挠度较大、稳定性较差、易产生振动噪声等缺陷,而通常选择在板壳结构上布置加强筋,以增加少量材料的代价显著提高结构的静动态稳定性,降低结构的振动及声辐射,减少机械噪声。传统的加强筋布置方式未经过系统的优化设计,一般是保守的规则分布。近年来随着以材料分布为目标的拓扑优化理论的不断完善,加强筋分布设计问题被转换为材料的分布问题,如将均匀化、渐进优化、变密度等拓扑优化方法应用到加强筋的分布优化设计中[1~4]。但是采用这些方法不仅易出现棋盘格式、网格依赖性、局部极值等问题,而且由于其为连续拓扑优化方法,所得结果是结构加强的区域,需要经过设计者的处理才能转换成最终的布局方案,应用受限。采用仿生物组织结构形态设计的离散拓扑优化方法为问题的解决提供了一个新的思路。丁晓红等基于植物根系形成机理提出自适应成长技术对加筋板的布局进行了优化[5],并以提高基频为优化目标进行了抗振优化设计[6],薛开等根据植物叶脉脉序形成的结构力学提出了仿生脉序生长算法对板壳结构进行了加强筋分布设计[7]。目前已有的离散拓扑优化方法多为对板壳结构加强筋分布的静力和模态频率优化设计,针对动态响应如振动声辐射等的研究比较少[8]。
本文将叶脉脉序形成机理应用于基于声辐射优化的板壳结构加强筋分布布局优化问题中,提出了一种加强筋仿叶脉布局的声辐射优化算法,对板壳结构加强筋的布局进行了研究。
1 加强筋仿叶脉分布原理
利用仿生技术进行产品的设计往往可以突破现有工程设计中的瓶颈,使产品获得最佳的性价比,这是由于生物的组织结构和形态在其不断的进化中达到了最优的结果,因而在应用仿生技术进行产品设计之前,充分理解生物规律并建立从生物组织结构形态的形成机理到工程设计过程的联系显得十分的重要。
在植物叶脉脉序的生物性研究中,双子叶植物以等级和网状的脉序最具有代表性[9]。李永欣等对不规则加筋板与双子叶植物的相似性进行了分析[10],并进行了静载作用下加强筋的仿叶脉布局设计,获得了很好的结果。本文在其研究的启发下尝试将叶脉脉序形成机理应用于加强筋布局的声辐射优化问题之中。
双子叶植物脉序具有明显的拓扑特点。从宏观几何拓扑的角度来看,双子叶植物脉序主要有以下特点:
1) 叶脉是由不同直径的脉络构成的分级结构。主脉是最粗且最早生长的,从根部延伸到边缘顶端,分布形式与叶片的形状有关;次脉在主脉两侧分布,直径相对主脉要细小一些。
2) 脉络趋向于形成闭环和网状结构,次脉从主脉处开始生长,在接近边缘处和其他次脉或主脉形成闭环。
3) 在形成叶脉的过程中,叶片中的脉络结构大致保持均匀分布。
本文研究的是板壳结构加强筋仿叶脉布局优化问题,为了能够合理、充分地利用脉序生长规律,首先应该对植物脉序规律进行总结,并以此为基础形成加强筋的仿生形态力学模型;其次为了有效地模拟叶片的脉序,在离散板梁结构上对布局优化模型进行描述;最后利用仿叶脉布局优化方法指导结构的优化设计。以上3个步骤便是描述加强筋仿叶脉分布原理的仿生、结构、算法3个部分。加强筋仿叶脉分布原理如图1所示。可以看出,板梁理论模型是研究基础,植物脉序规律是关键,而仿叶脉的布局优化方法是主体。
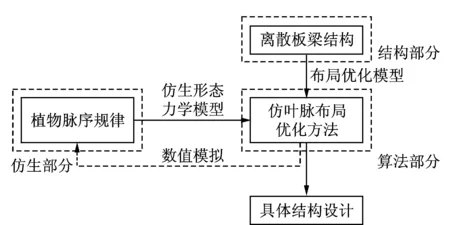
图1 加强筋仿叶脉分布原理
2 加筋板振动声辐射模型
对于加筋板壳结构,振动声辐射功率为
(1)
单频振动时有
(2)
式中R为结构上的点,Is为点声强,P(R)和Vn(R)分别代表声压和法向振动速度,T表示转置;*表示共轭。
对处于无限大障板上的板,利用Rayleigh积分公式可以得到板表面任一点声压与法向速度的关系为
(3)
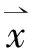
(4)
因此,加筋板声辐射功率可以表示为
(5)
利用四节点等参单元对结构进行离散,划分为Ne个单元,N表示等参单元的形函数,Pel和Vel分别为单元节点的声压向量和法向振速向量,则结构的声辐射功率又可表示为
(6)
3 加强筋仿叶脉分布声辐射优化算法
3.1 优化模型的建立
本文采用有限元方法对板壳加筋结构进行振动分析。加筋板的有限元模型为板梁离散模型,结构的单元刚度矩阵与单元质量矩阵分别由板单元和考虑偏心的梁单元的刚度与质量矩阵组成。
在优化算法中,结构中所有离散的节点被视作加强筋的待生长点,每个节点在生长时只与其附近的节点建立联系。对薄板上加强筋的布局优化主要是对加强筋所处的位置和加强筋尺寸参数进行设计,以便获得合适的离散集合,从而使结构的声辐射最小化,该集合包含加强筋分布的节点顺序集合和加强筋尺寸参数的离散集合。同时,为了满足结构性能要求以及结构的轻量化要求,还必须确定合理的约束条件,包括声学性能要求、力学性能要求、重量要求等。因此,薄板加强筋布局的声辐射优化模型可以表示如下:
(1)目标函数
采用结构声辐射功率作为优化模型的目标函数,考虑到结构声辐射功率是频率的函数,其大小随着频率的变化而变化。因此对声辐射功率在一个频段内的优化应该视作对这一频段内的平均声辐射功率进行优化,这样对某一频段的声辐射功率进行优化的目标函数可以用如下平均声辐射功率来表示
(7)
式中W(ω)表示在频率ω处的声辐射功率,ω1和ω0分别为优化频段的上下限。
(2)设计变量
在结构优化中以加强筋节点的有序集合和加强筋的宽度尺寸作为设计变量,其设计域分别为加强筋节点的任意序列集合和加强筋尺寸参数限制区间,可以将设计变量表示如下
(8)

(3)约束函数
以结构响应和重量限制为约束函数,则分别体现为对单元或者节点的应力值、结构的重量等约束,可以将约束函数表示如下
(9)
式中G0为重量的最大许用值,h1和h0分别为结构响应的上下限。
3.2 加强筋生长准则
加强筋仿叶脉分布设计的关键在于合理地将植物脉序规律应用于加强筋的生长规则之中,本文在进行加强筋的生长时采用从主脉到次脉的脉序生长形式,其生长准则如下:
(1)主脉生长准则
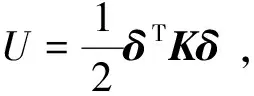
本文采用板梁组合模型进行加筋板结构分析,结构的变形能由弹性变形能和耦合能组成。由于模拟加筋薄板的板-梁组合结构为离散结构,结构耦合能量为零,因此结构的变形能可以用弹性变形能来表示。
在优化频带内,变形能均值可以表示为
(10)
因此,在一个板壳元上增加一个新梁元的应变能对体积增量的灵敏度可以表示为
(11)
式中K为单元整体刚度矩阵,由板壳单元刚度矩阵和偏心梁元刚度矩阵组成。
这样,待生长点的应变能灵敏度所成集合{α1,α2,…,αn}中的最大值对应的待生长点就是下次主脉的生长点。
(2)次脉生长准则
在脉络形成的重塑时期,剪应力对于分岔处脉络的几何平衡关系起着决定性的作用。粘性较大的脉细胞壁导致了脉细胞和基细胞间切向拉伸力的产生,此拉伸力使得脉细胞的方向稍作调整,最终满足矢量平衡关系[17]。在结构力说看来,叶脉的生长与树干纤维分布一样[18],都是为了消除剪应力,因此可采用剪应力灵敏度作为次脉生长准则。
考虑优化频率范围内三向应力状态下生长点i周围的局部剪应力τi,其表达式为
(12)

其对体积的灵敏度为
(13)
在待生长点的剪应力灵敏度组成的集合{β1,β2,…,βn}中选择最大值点作为次脉的下一个生长点。
3.3 优化流程
基于声辐射最优的板壳结构加强筋布局优化流程如图2所示。首先建立结构的有限元模型,得到优化频带内的应变能和剪应力等生长准则所需物理量,同时对算法中基本参数进行优化设置;其次根据自适应成长设计法中关于种子选取的结论[5],在确定种子位置时,主脉种子位置优先选择在载荷作用点,边界交接点和边界中点,次脉种子位置则选择在主脉上的剪应力极值点。主、次脉的生长严格按照生长准则进行,在继续生长之前需要更新加强筋生长环境,而终止条件则包括:遇到边界,满足收敛精度,达到体积约束量等。最后的脉序化简则是采用最小二乘法拟合加强筋的形线,并结合加强筋分岔点处各条脉络的宽度向量所组成的矢量平衡方程:Ri=-(R1+R2+…+Ri-1+Ri+1+…+Rn)来确定加强筋宽度。对于少数无法直接确定宽度的筋脉还应进行局部的长度、宽度和角度的调整,以达到要求。

图2 声辐射优化流程
4 数值算例及分析
为了验证本文算法的合理性,基于声辐射最优分别对典型四边固支的方板和矩形板进行加强筋布局优化设计,并对结果进行讨论分析。
4.1 四边固支方板
中心受集中载荷的四边固支方板如图3所示,方板边长L=0.8 m,厚度t=0.01 m,加强筋的主脉初始宽度为0.01 m,高度0.016 m,次脉宽度为0.005 m,高度与主脉相同。简谐激励幅值F=1 N,结构材料均为钢,密度ρ=7 800 kg/m3,弹性模量E=2.1×1011Pa,泊松比为0.3,声速为340 m/s,空气密度为1.225 kg/m3,声功率参考值取W0=10-12W,优化频段范围为0~1 200 Hz。

图3 四边固支方板
主脉生长初始种子的位置选择在载荷作用点,次脉生长的种子位置则选择在主脉上的剪应力极大值点,由于边界条件及载荷作用位置具有对称性,因而种子成对称生长。根据算法优化设计得到原始的加强筋分布如图4(a)所示,主脉由中心处的种子位置向四边延伸,次脉则是在主脉上开始分支,一直生长到边界处,整体的分布类似与植物叶脉的脉序形态。图4(b)为经过脉序简化后的加强筋最终布局,各段脉络的宽度尺寸在得到合理地调整之后可以用集合表示为{0.020 5 m,0.012 6 m,0.01 m,0.005 m,0.002 1 m},在图中采用脉络的相对粗细进行表示。可以看到,通过对脉序分布的拟合并进行矢量平衡,同时对局部区域进行微调,最终布局充分的保持了原始分布形态特点,是对原有布局的合理简化。
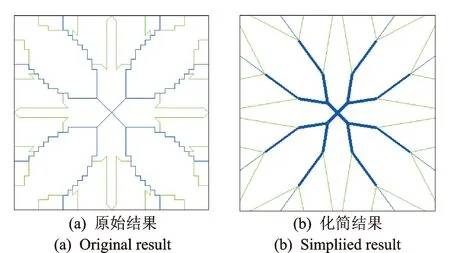
图4 加强筋布局结果

图5 传统加筋布局方板
考虑到目前传统的声辐射优化加筋方式多为正交,等间距,垂直排列等规则加筋,因此将最终布局结果的声辐射性能与采用相同体积约束量的传统加筋布局方板(如图5所示)进行比较,结果曲线对比如图6所示。从整个优化频带来看,声辐射功率峰值相对于优化前降低并且向高频方向移动,这是结构刚度得到提高,振动得到抑制,模态频率增加的结果;同时本文方法所得声辐射结果要优于传统加筋方法,考虑到前面的形态分布结果,可以认为本文提出的优化方法是正确的。

图6 声辐射功率曲线对比
4.2 四边固支矩形板
矩形板中心点受垂直板面向外的简谐载荷作用,其四边固支,如图7所示。矩形板长L=0.6 m,宽B=0.4 m,厚t=0.001 5 m,加强筋主脉初始宽度为0.001 5 m,高度0.01 m,次脉宽度为主脉一半,高度与主脉相同。简谐激励幅值F=4 N,结构材料均为钢,密度ρ=7 800 kg/m3,弹性模量E=210 GPa,泊松比μ=0.3,声速340 m/s,空气密度1.225 kg/m3,声功率参考值取W0=10-12W,优化频带范围为1 000~1 400 Hz。

图7 四边固支矩形板
主脉种子位置在载荷作用处,次脉种子为主脉的剪应力极值点。得到的加强筋分布原始结果如图8(a)所示,由于几何和力学特性以及优化频带范围的差别,矩形板所得结果与前面方板结果有着显著的差异,但它们仍然有着相同的特点,即加强筋的形态分布类似叶脉的脉序,这充分验证了本文方法利用植物脉序规律的合理性。

图8 加强筋布局结果
图8(b)为经过脉序简化后的结果,各段脉络的宽度尺寸在得到合理地调整之后可以用集合表示为{0.004 3 m,0.001 5 m,0.001 2 m,0.000 75 m},在图中则采用脉络的相对粗细进行表示。将其与图9所示的文献[8]优化结果进行对比分析,其声辐射功率对比曲线如图10所示。从图10可以看出,采用本文方法所得结果有效降低了优化频段内的峰值,虽然在局部频带内声辐射功率大于文献优化解,但从整个优化频段来看对声辐射性能的改善相对文献解优化来说是较为明显的,因此可以认为采用本文方法进行加强筋布局的声辐射优化设计是合理有效的。

图9 文献[8]加筋布局优化结果

图10 声辐射功率曲线对比
5 结 论
针对目前声辐射最优板壳结构加强筋布局优化问题的相关研究较少的现状,提出了一种基于植物叶脉脉序分布规律的加强筋布局优化设计方法。本文方法基于有限元和离散拓扑优化方法,并合理利用了植物脉序规律,适用于基于声辐射最优的板壳结构加强筋分布的优化设计。算例设计结果表明,加强筋的分布主次分明,与植物叶脉脉序形态保持一致,并且适于加工,整个优化频带内的声辐射功率降低,相对传统加筋和已有的其他方法改善的效果显著,本文方法可以应用于实际工程中的一些板壳结构优化。
参考文献:
[1] Ansola R, Canales J, Tarrago J A, et al. Combined shape and reinforcement layout optimization of shell structures [J]. Structural and Multidisciplinary Optimization, 2004,27(4):219—227.
[2] Querin O M, Xie Y M, Steven G P. Evolutionary structural optimization (ESO) using a bi-directional algorithm[J]. Engineering Computations, 1998,15:1 031—1 048.
[3] 章胜冬, 杨刚军, 张卫红. 薄板结构加筋布局设计的渐进结构优化方法[J]. 现代制造工程, 2009,4:5—9.Zhang Shengdong, Yang Jungang, Zhang Weihong. Evolutionary structural optimization for stiffener layout problem of plate structures[J].Modern Manufacuring Engineering, 2009,4:5—9.
[4] Lam Y C, Santhikumar S. Automated rib location and optimization for plate structures[J]. Structural Multidisciplinary Optimization, 2003,(25):25—45.
[5] 丁晓红, 林建中, 山崎光悦. 利用植物根系形态形成机理的加筋薄壳结构拓扑优化设计[J]. 机械工程学报, 2008, 44(4):201—205.Ding Xiaohong, Lin Jianzhong, YAMAZAKI Koestu. Topology desigh optimization of stiffened Thin-wall shell structures based on growth mechanism of root system[J]. Chinese Journal of Mechanical Engineering, 2008, 44(4): 201—205.
[6] 丁晓红, 陈建来, 程莉. 抗振板壳结构的仿生拓扑优化设计方法[J]. 船舶力学, 2008, 12(1):125—130.Ding Xiaohong, Chen Jianlai, Cheng Li. A bionic approach of topology design optimization for vibration-proof plate and shell structures[J].Journal of Ship Mechanics, 2008, 12(1):125—130.
[7] 薛开, 李永欣. 板壳结构加筋布局的仿生脉序生长算法[J]. 哈尔滨工程大学学报, 2011, 32(9):1 262—1 266.Xue Kai, Li Yongxin. A bionic venation growth algorithm for a stiffener layout in plate /shell structure[J]. Journal of Harbin Engineering University, 2011,32(9):1 262—1 266.
[8] 丁舒涛.声辐射薄板的优化方法研究[D].上海:上海交通大学, 2010.Ding Shutao. Optimize approach for the acoustic thin-shell plane[D].Shanghai:Shanghai Jiaotong University, 2010.
[9] Xue Kai, Li Yongxin, Wang Weiyuan. Venation-like rib layout design in plate under bending loads[J]. Journal of Biomimetics, Biomaterials and Tissue Engineering, 2012, 13:31—40.
[10] Li Yongxin, Xue Kai. Mechanics in leaf venation morphogenesis and their biomimetic inspiration to construct a 2-dimensional reinforcement layout model[J]. Journal of Biomimetics, Biomaterials and Tissue Engineering, 2011, 10:81—93.
[11] Durand M.Optimizing the bulk modulus of low-density cellular networks[J].Physical Review E, 2005, 72(011114):1—5.
[12] Couder Y, Pauchard L,Allain C,et al.The leaf venation as formed in a tensorial field[J].The European Physical Journal B,2002,28:135—138.
[13] Durand M. Architecture of optimal transport networks[J]. Physical Review E,2006, 73(016116):1—6.
[14] Durand M. Low-density cellular materials with optimal conductivity and bulk modulus[A]. 18th French Congress of Mechanics[C]. Grenoble, 2007: 27—51.
[15] Kizilova N N. Computational approach to optimal transport network construction in biomechanics[J]. Lecture Notes in Computer Science, 2004,3044: 476—485.
[16] Kizilova N N. Long-distance liquid transport in plants[J]. Proceedings of the Estonian Academy of Sciences, 2008, 57(3): 179—203.
[17] Arezki Boudaoud. An introduction to the mechanics of morphogenesis for plant biologists[J]. Trends in Plant Science, 2010, 15(6): 353—360.
[18] Mattheck C. Design in Nature: Learning from Trees[M]. Berlin: Springer-Verlag Berlin Heidelberg, 1998: 129—139.

