椭圆轮廓度误差几何遍历搜索算法
雷贤卿,崔静伟,王海洋
(1.河南科技大学机电工程学院,河南 洛阳 471003;2.洛阳轴研科技股份有限公司,河南 洛阳 471003)
椭圆轮廓度误差几何遍历搜索算法
雷贤卿1,崔静伟2,王海洋1
(1.河南科技大学机电工程学院,河南 洛阳 471003;2.洛阳轴研科技股份有限公司,河南 洛阳 471003)
结合椭圆几何特性及其相关的评定问题的研究现状,提出了椭圆轮廓度误差的遍历搜索算法。该算法的原理是以最小二乘椭圆两焦点为初始参考点,按一定的规则分别布置一系列的网格点构造辅助焦点,依次以各辅助点为假定理想椭圆焦点,构造一系列的辅助椭圆作为假定理想椭圆。计算测量点到这些假定理想椭圆的距离极差,最终实现椭圆轮廓度误差的最小区域评定。实例验证表明:该算法可以有效、正确地评定椭圆轮廓度误差。
误差评定;椭圆度;遍历搜索算法;最小区域
0 引言
椭圆轮廓度的公差带是与理想椭圆等距的两个椭圆等距线之间的区域。对于其轮廓的几何参数和轮廓度误差等的评定方法,国家标准尚未做出明确的规定和说明。但椭圆形零件在特殊场合的应用,如发动机活塞的裙部设计成中凸变椭圆形状,以保证其吸能效果,这就使得椭圆线轮廓度精密测量及精确评定有着重要的价值。但关于椭圆轮廓度误差的评定,国家和国际标准都没有给出一种特定的评定算法。近年来椭圆轮廓度误差的评定方法主要是运用最小二乘法,但最小二乘法的计算误差较大,不能进行精确评定,很难符合实际测量的要求。不少学者都进行了椭圆轮廓度误差评定的研究,比较有代表性的算法有:基于代数距离的最小二乘法[1-5],正交最小二乘法[6],矢函数法[7],采用对应特征点法、一维搜索法(DFP)及一维搜索法的自适应调整的线轮廓误差评定方法[8],最小方差估计拟合算法[9],椭圆直接拟合算法[10],最大内接椭圆法,最小外接椭圆法[11]。这些评定方法对于椭圆轮廓度误差的评定都有一定的作用和效果。
本文结合椭圆轮廓度误差几何特性及其评定问题,提出了几何遍历搜索的椭圆轮廓度误差最小区域评定算法,该算法可以有效、准确地评定椭圆度误差。
1 几何遍历搜索算法的原理
首先通过椭圆轮廓上测量点的坐标值,以一定方法(如最小二乘法)确定参考椭圆,计算所有测量点到参考椭圆的距离极差值(椭圆轮廓度误差,记为 e0)。如图 1所示,以参考椭圆的两焦点F1(x01,y01)、F2(x02,y02)为初始参考点,在其周围以定边长f(如最小二乘椭圆度误差值或估计的椭圆度误差值)分别布置一个正方形为搜索区域,将正方形区域的边长分别进行n等分,并对搜索区域进行网格划分,可得两组(n+1)2网格点,(n+1)4对辅助点(即新的焦点坐标),计算测量点到辅助点所确定的假定理想椭圆的误差值echa,可得到(n+1)4个echa,其中这(n+1)4个echa中的最小值记为e1。比较e0和e1的大小,根据椭圆度误差的定义可知:e0和e1中较小值就是被测椭圆的最小区域椭圆度误差。
2 几何遍历逼近算法的步骤
设椭圆轮廓上测量点的坐标值为:pi(xi,yi), (i=1,2,…,N)。
2.1 构造辅助点
以最小二乘椭圆的焦点坐标F01(x01,y01)、F02(x02,y02)为初始参考点(椭圆轮廓度误差的最小二乘评定算法在许多参考文献中均有详细的介绍,本文不再重复)。以最小二乘椭圆轮廓度误差或估计的椭圆轮廓度误差值e0为定边长f(f=e0)构造正方形区域,对每个正方形区域的边长进行n等分的网格划分,得到两组(n+1)2个网格点,将两组网格点进行组合可得(n+1)4对辅助点。
辅助点坐标按式(1)~式(4)进行计算:首先,利用式(1)计算出正方形左上角的辅助点坐标Fv1(xv1,yv1)、Fv2(xv2,yv2)作为计算基点:

图1 椭圆度误差几何遍历搜索评定原理

以计算基点为参考点,利用式(2)和式(3)计算辅助点坐标Fv1(p,q)(xv1(p,q),yv1(p,q))、Fv2(p,q)(xv2(p,q),yv2(p,q)),(p,q=1,2,…,n+1):

2.2 构造辅助椭圆
以辅助点Fv1(p,q)(xv1(p,q),yv1(p,q))(p,q=1,2,…,n+1)依次与辅助点Fv2(p,q)(xv2(p,q),yv2(p,q))(p,q=1,2,…,n+1)组合可得到(n+1)4对假定理想椭圆焦点坐标,可构造出(n+1)4个辅助椭圆。由椭圆的几何特性可知:椭圆可以用下列5个独立参数来唯一确定,长轴半径、短轴半径、中心坐标及长轴与x轴的夹角。
(Ⅰ)长轴半径aj(j=1,2,…,16)的确定。仅由两焦点坐标无法确定一个椭圆,由椭圆定义可知:椭圆上的点到两焦点坐标的距离之和为长轴半径的2倍,本文利用测量点的坐标值,用式(5)计算所有测量点pi(xi,yi)(i=1,2,…,N)分别到这(n+1)4对焦点的距离dij(j=1,2,…,(n+1)4),作为(n+1)4个辅助椭圆的长轴值。辅助椭圆长轴半径值aj(j=1,2,…,(n+1)4)利用式(6)取所有测量点所确定的长轴半径值的平均值。

(Ⅱ)短轴半径bj(j=1,2,…,(n+1)4)的确定。利用式(7)根据两焦点坐标计算辅助椭圆的焦距。由椭圆长、短半轴间的关系按式(8)确定短轴半径。
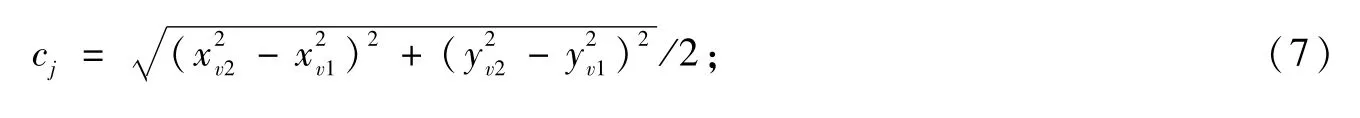

(Ⅲ)中心坐标x0j、y0j(j=1,2,…,(n+1)4)的确定,由椭圆位置的几何关系可得:

(Ⅳ)长轴与x轴的夹角θj(j=1,2,…,(n+1)4)的确定:

由以上得到椭圆主参数,则辅助椭圆的方程可表达为:

设椭圆的一般方程为x2+Axy+By2+Cx+Dy+E=0,将式(12)展开,计算假定理想椭圆的一般方程系数:

可得到(n+1)4个辅助椭圆方程x2+Ajxy+Bjy2+Cjx+Djy+Ej=0,j=1,2,…,(n+1)4。
2.3 计算测量点到辅助椭圆的距离极差
设点Mij(Xij,Yij)为过测量点pi(xi,yi),(i=1,2,…,N)的椭圆法线与辅助椭圆的交点,由于交点Mij(Xij,Yij)既在法线上又在辅助椭圆上,即点Mij(Xij,Yij)满足方程组(14):

用式(15)计算所有测量点到(n+1)4个辅助椭圆的距离,其中测量点在辅助椭圆外侧的最大距离与内侧的最小距离之差为椭圆度误差echaj,即式(16)。

有(n+1)4个辅助椭圆就可以得到(n+1)4个距离极差值echaj,根据椭圆度误差的定义可以知道,(n+1)4个距离极差值中的最小者min echaj即为被测椭圆的最小区域椭圆度误差,用F表示。

3 实例验证
表1为文献[6]中的椭圆的测量数据,利用本文所提算法对同一组数据处理结果比较,验证椭圆度几何遍历搜索算法的正确性。设定初始条件如下:
(Ⅰ)初始参考点坐标:用最小二乘法计算的椭圆焦点坐标为F1(-11.283 1,-21.423 3)、F2(11.284 0,81.425 5)。
(Ⅱ)扩展区域的初始边长:f=e0(最小二乘法计算出的椭圆度误差值e0=0.004 9 mm)。
(Ⅲ)扩展区域划分的网格点数:每个扩展区域划分的网格点数为k(k分别取25,100,225,400),则组成k2对椭圆焦点坐标来进行计算。
数据处理结果见表2,与其他文献中不同方法计算结果比较见表3。

表1 测量数据 mm

表2 数据处理结果

表3 不同方法的计算结果比较
由表2和表3可以看出:本文提出的椭圆轮廓度几何遍历搜索算法结果与文献[7]的计算结果中椭圆的主参数相一致,且评定结果更精确。
由表2可以看出:在使用本算法时,初始区域一定的情况下,网格点划分越多,得到的误差值呈现出越来越小的规律,所以算法是收敛的。当 k≥100时,所计算出的椭圆轮廓度误差值之间相差小于0.000 1 mm,说明算法具有良好的稳定性。所以在实际应用划分网格时k≤100即可。这就说明几何遍历误差最小区域评定算法可以有效、准确地评定椭圆轮廓度误差。
4 结束语
结合椭圆度误差的几何特性,研究了椭圆轮廓度误差的几何遍历搜索算法。该算法对测样点是否均匀没有要求,其原理简单,易于编程。应用文献[7]的测量数据,将几何遍历搜索算法应用于椭圆度误差评定中,在每个搜索区域划分网格点数分别为100时,计算结果分别比最小外接椭圆法[10]、最大内接椭圆法[10]、矢函数法[6]计算的结果减小了2.6μm、2.9μm和3.0μm。计算结果证明:几何遍历搜索算法能够有效地对椭圆轮廓度误差进行精确评定,对三坐标测量机上椭圆轮廓度误差的评定具有一定的借鉴作用。
[1] 崔静伟,雷贤卿,王海洋,等.基于最小二乘法的平面任意位置椭圆轮廓度误差的精确计算[J].制造业自动化,2013,35(2):114-115,146.
[2] Sung J A,Wolfgang R,Hans-Jurgen W.Least-squares Orthogonal Distances Fitting of Circle,Sphere,Ellipse,Hyperbola,and Parabola[J].Pattern Recognition,2001,34:2283-2303.
[3] 邹益民,汪渤.一种基于最小二乘的不完整椭圆拟合算法[J].仪器仪表学报,2006,27(7):808-812.
[4] 刘书桂,李蓬,那永林.基于最小二乘原理的平面任意位置椭圆的评价[J].计量学报,2002,23(4):245-247.
[5] 马前南,李航,刘丽丽,等.最小二乘改进算法及其在椭圆拟合中的应用[J].河南科技大学学报:自然科学版,2014,35(3):18-21.
[6] W ijewickrema S,Esson C,Charlesl P A.A Novel Approach to Orthogonal Distance Least Squares Fitting of General Conics[C]//ISA.2009:138-145.
[7] 侯宇,张竞,崔晨阳.复杂线轮廓度误差坐标测量的数据处理方法[J].计量学报,2002,23(1):12-16.
[8] 张琳,郭俊杰,姜瑞,等.自由曲线轮廓度误差评定中的坐标系自适应调整[J].仪器仪表学报,2002,23(2):203-206.
[9] Cui Y T,John W,Herbert R.Estimation of Ellipse Parameters Using Optimal Minimum Variance Estimator[J].IEEE Trans PAMI,2002,24(5):620-638.
[10] Fitzgibbon A,Pilu M,Fisher R B.Direct Least Square Fitting of Ellipses[J].Pattern Analysis and Machine Intelligence 1999,21(5):476-480.
[11] 李秀明,石照耀.基于方程的椭圆轮廓度的评定[J].北京工业大学学报,2009,35(10):1303-1307.
TH161
A
1672-6871(2014)06-0009-05
国家自然科学基金项目(50875076);河南省基础与前沿技术研究计划基金项目(122300413209,122300410114)
雷贤卿(1963-),男,河南洛宁人,教授,博士,硕士生导师,主要从事精密测试技术方面的研究.
2014-03-28

