油浸式电力变压器系统的数值优化

邵志伟，黄亚继，刘明涛

（1.东南大学能源热转换及其过程测控教育部重点实验室，江苏 南京 210096；2.江苏省电力设计院，江苏 南京 211102）

油浸式电力变压器系统的数值优化

邵志伟1，黄亚继1，刘明涛2

（1.东南大学能源热转换及其过程测控教育部重点实验室，江苏 南京 210096；2.江苏省电力设计院，江苏 南京 211102）

为了改善油浸式变压器通风系统的散热效果，按照正交试验方法设计工况，利用计算流体力学方法，对油浸式变压器系统中散热器室通风进行了数值模拟。通过改变影响散热的参数，分析了各参数对散热效果的影响规律。研究结果表明：机械进风口宽度对散热效果的影响最为显著，机械进风口位置和机械通风速率的影响次之，自然通风速率的影响最小，并在此基础上提出了优化参数组合方式。

油浸式电力变压器；数值优化；正交试验

0 引言

随着经济的快速发展，高电压、大容量的变电站深入市区，但根据《城市电力网设计导则》要求，变电站的建设必须与周围环境相协调，因此，不得不将变电站转移至户内甚至地下。油浸式电力变压器具有承受负载大、噪音小和结构简单等优点，在电力系统中得到了广泛使用。油浸式变压器的冷却主要是通过片式散热器来实现的，油泵将变压器上部高温油送入散热器内，再由翅片将热量传到空气中通过自然对流散失［1－5］。

散热器表面热点温度和散热效率是评价油浸式变压器通风系统散热效果优劣的两个重要指标，受自然通风速率、机械通风速率、机械进风口宽度与机械进风口位置因素的影响，但近年来国内外学者在该领域的研究鲜见报道［6］。为了获得上述影响因素之间的关系，本文提出了一种油浸式变压器混合通风的优化方法，首先，采用Fluent软件对散热器通风的多个工况进行了数值模拟；然后在正交试验思想指导下，通过改变各影响因素进行多工况模拟，分析了各因素对散热器温度降低的影响，并提出优化的参数组合方式［7－8］。

1 散热器数值模拟

1.1 几何模型

图1为油浸式变压器通风系统示意图。由图1可知：散热器和变压器分体布置在相邻房间内，变压器室和散热器室由变压器室通风口连通。油浸式电力变压器通风系统运行时，冷风通过变压器室自然进风口和散热器室自然进风口分别进入变压器室和散热器室，最终由散热器室排风口排出。本文重点研究油浸式电力变压器通风系统中散热器室自然通风速率、机械通风速率、机械通风口位置、机械通风口宽度对散热效果的影响规律，首先通过Gambit建立数学模型，再利用Fluent进行数值计算，最后在正交思想指导下研究各因素之间的影响关系，并得到最佳参数组合。油浸式通风系统各参数见表1。

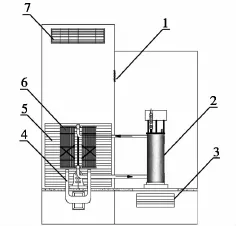
图1 油浸式变压器通风系统示意图

变电站实际运行过程中，空气在散热器内部通道中的流动是三维、非定常、可压缩黏性流体的流动过程。但由于计算机内存限制和计算时间合理性等问题，完全模拟散热器内部的流场是十分困难的，在一定误差允许范围内可对模型作适当简化［9］。

表1 油浸式变压器通风系统参数

1.2 控制方程

1.2.1 质量守恒方程

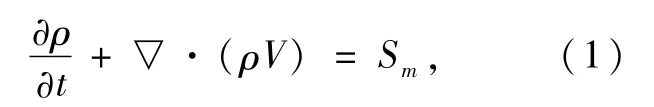
式中，ρ为密度；t为时间；V为速度矢量；源项Sm为加入到连续相的质量。

1.2.2 动量守恒方程

式中，p为流体微元体上的静压力；V为速度矢量；g和F分别为作用在微元体上的重力体积力和其他外部体积力；τ为因分子黏性作用而产生的在微元体表面上的黏性应力张量。

1.2.3 能量守恒方程

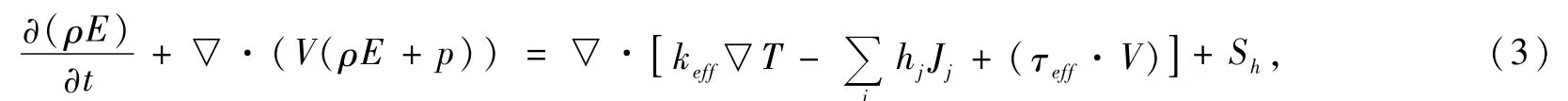
式中，E为流体微团的总能；Jj为组分j的扩散通量；方程右边前3项分别为由于导热、组分扩散和黏性耗散所引起的能量传递；Sh为热源项。

1.2.4 k-ε方程

k湍流动能输运方程：

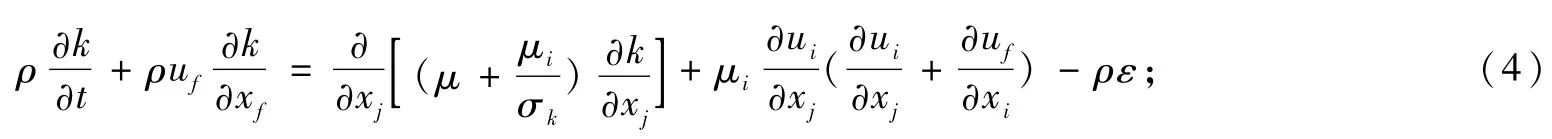
ε湍流动能输运方程：

式中，常数值c1＝1.44；c2＝1.92；cμ＝0.09；σk＝1.0；σε＝1.3。

1.2.5 Navier-Stokes方程

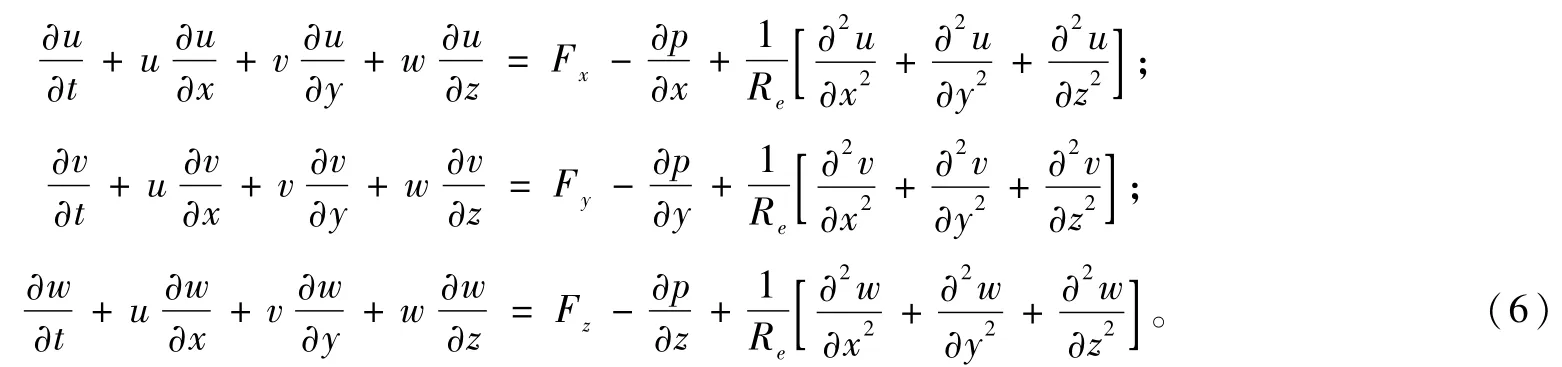
选用标准的k-ε方程求解湍流对流换热问题时，控制方程满足质量守恒方程、动量守恒方程、能量守恒方程、N-S方程［10］。

1.3 计算条件及网格划分

采用Fluent6.3.26商用软件作为计算平台，用Gambit软件生成网格，对整个计算区域采用分块划分、局部加密的原则进行划分，网格为四面体非结构化布置，以保证计算精度，散热器附近区域网格尺寸为0.05 mm，数目约为2.3×106，散热器以外区域网格尺寸为0.15 mm，数目约为2.1×106。介质采用密度为1.2×103kg／m3、运动黏度为1.84×106Pa·s的空气。散热器通道间气流场采用SIMPLE算法计算，入口截面速度均匀分布，出口类型采用Outflow，壁面无滑移绝热［11］。

1.4 正交试验设计

散热器室通风散热与自然通风速率、机械通风速率、机械进风口宽度和机械进风口位置参数密切相关。为了更加全面地研究3种不同水平下所有因素的影响特性，采用正交试验设计，基于数理统计学原理科学合理的安排试验，并按一定规律分析处理试验结果，从而能较快判断诸多因素中何种因素是主要因素，以及判断影响因素之间的相互影响情况，是分析因素设计的一种快速、高效、经济的试验设计方法［12］。本文按照“四因素三水平”正交试验设计，采用正交表L9（34）安排，共需9次CFD数值模拟试验，试验设计方案如表2所示，不考虑各因素之间的交互作用。其中，A表示自然通风速率v，m／s；B表示机械通风速率V，m／s；C表示机械进风口距离d，mm；D表示机械进风口宽度S，mm。

表2 模型变量与试验工况

2 模拟计算结果与分析

本文建立的油浸式变压器通风系统特性模型，不仅考虑了机械进风口宽度和位置影响，还考虑机械通风速率和自然通风速率因素的影响，下文着重分析不同因素对散热器散热特性的影响规律。散热效率E指排出室内热量的快慢程度，E越大表明散热效果越好［13］。

定义

式中，Tp为平均排风温度；Tn为人员活动区平均温度；T0为进风温度。

2.1 各参数对温度变化的影响

图2给出了V＝1.0 m／s，d＝200 mm，S＝400 mm不变时，各截面最高温度随自然通风速率的变化关系。由图2分析可知：随着距离进风口越来越远，散热器温度呈升高趋势，不同自然通风速率下变化趋势基本一致，其中自然通风速率v＝0.4 m／s时，散热器整体温度较低，不超过55℃。主要原因为：距离进风口越远，气流在散热器内部的扰动变得越弱，空气侧对流换热系数变小，导致散热效果变差，温度升高；自然通风速率增大，导致外部更多新风进入，减小空气龄，换气次数增加，散热器处在更多新风的包裹中，因此较大的自然通风速率有利于散热器散热，但影响效果有限。

图3给出了v＝0.4 m／s，d＝300 mm，S＝400 mm不变时，各截面最高温度随机械通风速率的变化关系。由图3可以得到：机械进风速率在1.0～2.0 m／s变化时，同一截面散热器温度均有大幅下降，温度维持在33～47℃。分析其原因是：在散热器下方加强机械通风，速度的提高造成对散热片的冲刷加强，破坏表面的热边界层，导致空气在散热器通道内扰动增强，提高局部换热系数，造成散热器整体温度呈下降趋势。

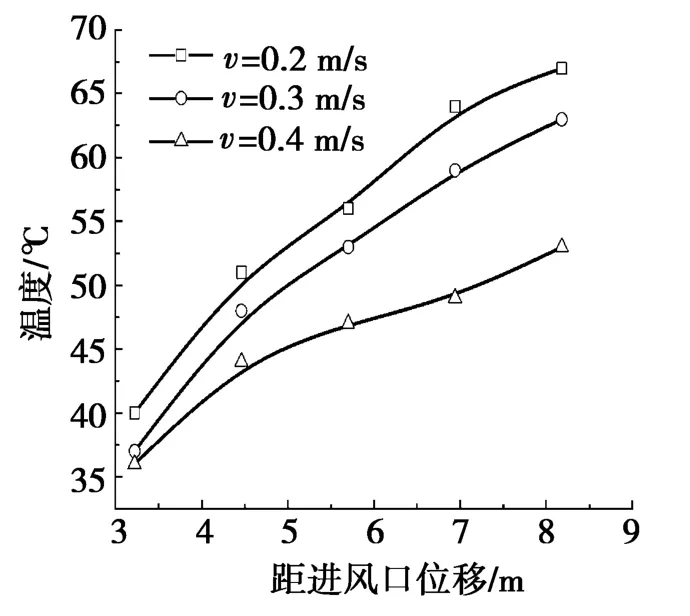
图2 不同自然通风速率下的温度分布

图3 不同机械通风速率下的温度分布

图4给出了v＝0.3 m／s，V＝1.0 m／s，S＝400 mm不变时，各截面最高温度随机械通风口位置的变化关系。由图4可以得到：机械进风口距散热器底部d＝200 mm变化到d＝400 mm时，同一截面散热器温度均有所下降，温度维持在35～52℃。其原因可能是：机械进风口距离散热器越远，射流流程增加，会卷吸更多冷空气进入散热器内部，在散热器下方周围形成负压区，掺混更多的冷空气形成漩涡，破坏散热片表面热边界层，导致热阻减小，造成散热器整体温度呈下降趋势。

图5给出了v＝0.3 m／s，V＝1.0 m／s，d＝400 mm不变时，各截面最高温度随机械通风口宽度的变化关系。由图5可以得到：机械进风口距散热器底部S＝400 mm变化到S＝800 mm时，同一截面散热器温度下降较为明显，温度维持在33～50℃。其主要原因是：随着机械进风口宽度S增大，一方面，单位时间内的机械通风量增加，气流循环加快，热空气能较快排出；另一方面，机械进风口的吹扫面积也会相应增大，强制对流换热的接触面积变大，对流换热能力加强，导致散热器整体温度呈降低趋势［14－17］。

图4 不同机械进风口位置下的温度分布

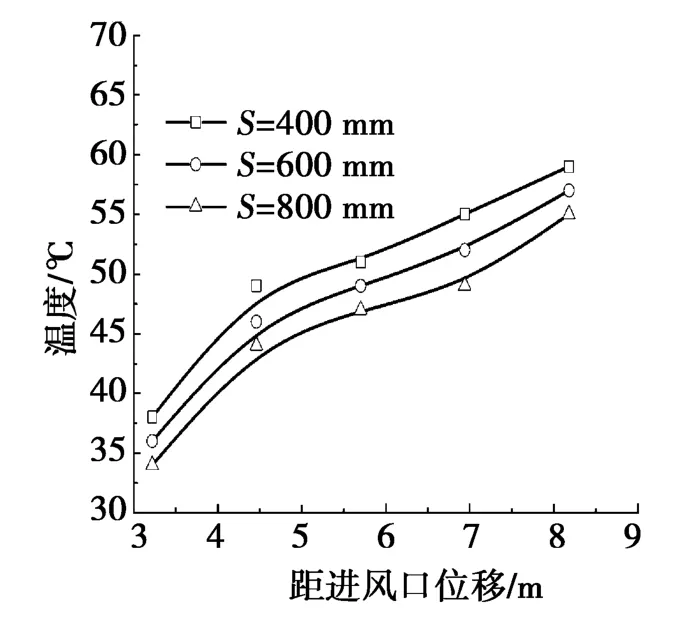
图5 不同机械进风口宽度下的温度分布

2.2 各参数对散热效率的影响

针对V＝1.0 m／s，d＝200 mm，S＝400 mm不变工况条件下，可得到E随v的变化关系：随着自然通风速率从0.2 m／s增加至0.5 m／s时，相应的排热效率由1.37增大至1.95，排热效率基本呈上升趋势，自然通风速率较小或较大时，散热效率变化均趋于平缓。原因是散热器室内气流的空气龄大小与自然通风速率密切相关，自然通风速率在0.2～0.3 m／s变化时，对排热效率的影响不大；自然通风速率大于0.4 m／s时，受限于散热器其他参数影响，排热效率增幅趋于平缓。

针对v＝0.4 m／s，d＝300 mm，S＝400 mm不变工况下，可得到E随V的变化关系：随着机械通风速率从1.0 m／s增加至2.5 m／s时，相应的排热效率由1.39增大至2.09，排热效率增大的趋势较为明显。分析认为：机械通风速率越大，一方面可以增强散热器表面的气流扰动，减小空气侧热阻，增大表面换热系数；另一方面，可促使散热器内热气流快速排出，气流循环能力增强，从而造成散热器室排热效率呈增大趋势。

针对v＝0.3 m／s，V＝1.0 m／s，S＝400 mm不变情况下，可得到E随d的变化关系：随着机械通风口距离散热器越远，距离从200 mm增大至500 mm时，排热效率呈上升趋势，从1.43增加至1.84，但增幅趋于平缓。这是由于机械通风口离的越远，气体射流可卷吸周围更多的冷空气进行动量交换，使气流均匀地流过散热器，防止散热器内温度不均匀现象出现，提高排热效率。但当d＞400 mm后，射流流动过程中动量损失也相应增加，造成排热效率趋于不变。

针对v＝0.3 m／s，V＝1.0 m／s，d＝400 mm不变条件下，可得到E随S的变化关系：随着机械进风口宽度的增大，从400 mm逐渐增大至100 mm时，排热效率也相应增大，从1.78增大至3.74，近似呈线性关系。主要是因为：其他参数条件一定时，机械进风口宽度增加，对散热器的吹扫面积也相应增加，大大提高了强化对流换热的有效面积，大大提高了对流换热能力，因此造成排热效率大幅增加。相对另外3个影响因素而言，由于此时机械进风口的影响占主导地位，排热效率与机械进风口宽度近似呈线性关系［18－20］。

3 参数的优化分析

极差分析法简称R法，它具有计算简单、直观形象、简单易懂等优点，是正交试验结果分析最常用的方法，包括计算和判断两个步骤。

其中，Kjm为第j列因素m水平所对应的试验指标和为Kjm的平均值，由的大小可以判断j因素的优水平和各因素的优水平组合，即最优组合；Rj为第j列因素的极差，反映了第j列因素水平波动时，试验指标的变动幅度。Rj越大，说明该因素对试验指标的影响越大。Rj为第j列因素的极差，即j列因素各水平下的指标值的最大值与最小值之差，根据Rj大小，可以判断因素的主次顺序［11］。

表3为排热效率的极差分析，由表3可看出：机械进风口宽度是影响油浸式变压器通风系统散热的最重要因素，机械进风口距离和机械通风速率次之，自然通风速率的影响程度最小；优化组合为：自然通风速率0.4 m／s，机械通风速率2.0 m／s，机械进风口距离d＝400 mm，机械进风口宽度S＝800 mm。

表3 排热效率的极差分析

4 结论

（1）针对散热器散热特性影响因素水平多

的情况，使用正交试验方法设计模拟工况，科学安排模拟次数，可大大简化工作量。数值模拟结果表明：机械进风口宽度、机械通风速率、机械进风口位置和自然通风速率对散热器通风散热均有影响，但影响程度不同。

（2）根据正交试验结果极差分析，机械进风口宽度是影响油浸式变压器通风系统散热的最重要因素，机械进风口距离和机械通风速率次之，自然通风速率的影响程度最小，因此，选择合理的机械进风口结构参数是优化散热通风工作的关键。

（3）根据实际自然通风速率，合理选择和设计机械通风速率等其他参数，可以实现在总能耗降低的条件下达到更加理想的通风散热效果。

［1］ 李鹏飞，李国祥，胡玉平.大型油浸式自冷变压器冷却系统CFD分析［J］.变压器，2008，45（4）：45－48.

［2］ 丛龙飞，冯恩民，郭振岩，等.油浸风冷变压器温度场的数值模拟［J］.变压器，2003，40（5）：2－5.

［3］ 杜莉，王秀春.油浸式变压器内流场和温度场的数值模拟研究［J］.变压器，2012，49（1）：19－22.

［4］ Bassiouny R，Koura N S A.An Analytical and Numerical Study of Solar Chimney Use for Room Natural Ventilation［J］. Energy and Buildings，2008，40（5）：865－873.

［5］ 高春艳，梁坤峰，李军号，等.变压器室3种通风散热方案模拟研究［J］.河南科技大学学报：自然科学版，2013，34（3）：63－67.

［6］ 顾建明，连之伟，陆明琦.通风系统性能的评价［J］.暖通空调，2002，32（5）：100－101.

［7］ 陈勇，王旭，孙炳楠，等.单体房间室内通风多影响因素的试验研究［J］.浙江大学学报：工学版，2012，46（4）：658－664.

［8］ 唐超，高岩，李德英，等.基于正交试验的工业厂房自然通风影响因素数值分析［J］.建筑科学，2011，27（12）：81－86.

［9］ 郭娟，王汉青.基于Fluent的多元通风系统数值模拟分析［J］.流体机械，2013，41（5）：29－33.

［10］ 童莉，张政，陈忠购，等.机械通风条件下连栋温室速度场和温度场的CFD数值模拟［J］.中国农业大学学报，2003，8（6）：33－37.

［11］ Stephen R L，Andrew W W.Natural Ventilation of a Building With Heating at Multiple Levels［J］.Energy and Buildings，2007，42（3）：1417－1430.

［12］ 任露泉.试验设计及其优化［M］.北京：科学出版社，2009：238－242.

［13］ 蔡芬，胡平放.通风效率性能参数在通风设计中应用的探讨［J］.建筑热能通风空调，2005，24（1）：73－75.

［14］ Li Y G.Natural Ventilation Induced by Combined Wind and Thermal Forces［J］.Building and Environment，2001，36（1）：59－71.

［15］ 张霞，王秀春，郭晓霞.片式散热器各通道流量分布与散热能力CFD分析［J］.变压器，2011，48（3）：62－66.

［16］ Fracstoro G V，Mutanti G，Perino M.Experimental and Theoretical Analysis of Natural Ventilation by Windows Opening［J］.Building and Environment，2002，34（8）：817－827.

［17］ 万鑫，苏亚欣，杨艳超.工业厂房自然通风的数值模拟及结构改进［J］.中国安全科学学报，2008，18（8）：103－108.

［18］ Tan G，Glicksman L R.Application of Integrating Multi-zone Model With CFD Simulation to Natural Ventilation Prediction［J］.Building and Environment，2005，37（10）：1049－1057.

［19］ 万鑫，苏亚欣.建筑结构对带内热源工业厂房自然通风影响的数值研究［J］.暖通空调，2009，39（11）：60－64.

［20］Olivera E D，Goran T.Energy Efficiency Optimization of Combined Ventilation Systems in Livestock Buildings［J］. Building and Environment，2010，42（8）：1165－1171.

TK172

A

1672－6871（2014）04－0038－05

国家自然科学基金项目（51006023）

邵志伟（1987－），男，安徽阜阳人，硕士生；黄亚继（1975－），男，江苏南京人，教授，博士，博士生导师，研究方向为变电站通风优化.

2013－12－13