Harry-Dym方程的推广
王丽真,黄 晴,左苏丽
(西北大学数学系,陕西西安 710127)
研究方程的可积性是可积系统中的重要而基本的问题。在对称方法中,无穷多高阶对称的存在性或局部守恒律的存在性被认为是某种可积性的定义。这种方法的主要目的是得到容易被证实的可积性的必要条件,辨识可积的情形并给出可积系统的完全的刻画和分类。
本文研究推广的Harry-Dym方程
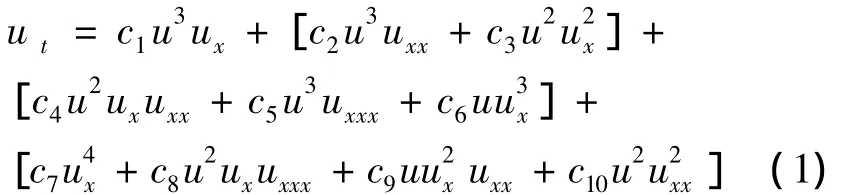
其中ci(i=1,2,…,10)为任意常数。当c5=1,其他常数取零时,方程(1)为Harry-Dym方程。这个由非线性项和耗散项耦合的方程是在表面张力的 Saffman-Taylor问题的分析中产生的[1]。Harry-Dym方程具有完全可积性,有孤子解,有Bäcklund变换,Painleve性质和无穷多个守恒律[2-4]。文献[5]利用直接方法给出了 Harry-Dym方程的Cusp型单孤子波解。利用Adomian分解、何氏变分迭代、直接积分及幂级数,文献[6]建立了Harry-Dym方程的行波解。文献[7-9]研究了Harry-Dym方程的其他性质。
文献[10-11]利用符号表示的方法研究了Camassa-Holm类方程并分离出了可积的情形。受此启发,本文中将Harry-Dym方程推广为四次齐次的三阶方程(1),并利用文献[11]中的方法分离出其中的可积方程类。
1 预备知识
1.1 基本定义
设R是关于 u,uxx,uxxx,… 的微分多项式在复数域C上的环。简单起见,记。环 R 是具有导数
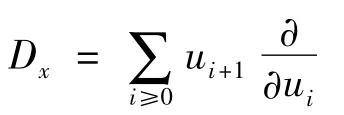
的微分环。这个环有一个自然的相对于u及它的关于x的导数的非线性程度的分级
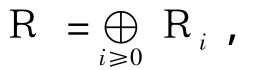
其中Ri={f(u,u1,…,uk)∈R|f(λu,λu1,…,λuk= λif(u,u1,…,uk)}λ∈C。空间R0=C,R1是关于 u,uxx,uxxx,… 的线性多项式的空间,R2是二次多项式的空间。记
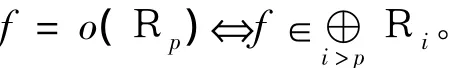
记R+为没有单位元的微分环
1)对于线性项ui∈R1,定义其符号表示为
2)对于二次项uiuj∈R2,定义其符号表示为

下面给出R上的加法、乘法和导数运算的符号表示形式。设f∈Ri,g∈Ri是两单项式,它们的符号表示分别为 f→(ξ1,…,ξi)和 g→(ξ1,…,ξj),则
Dx(f)→(ξ1,…,ξi)(ξ1+ … + ξi)。
对于符号表示中的算子Dx,定义特殊的符号η满足
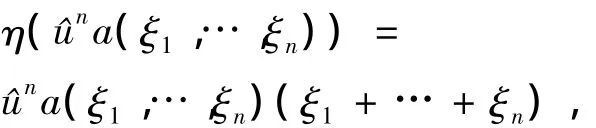
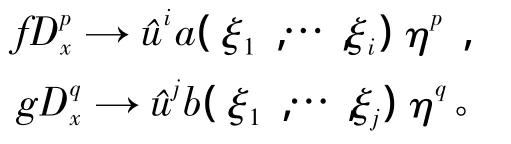
一般地,考虑级数

其中 ak(ξ1,…,ξk,η)是关于 ξ1,…,ξk的对称函数。其加法法则是显然的,而复合运算为…,
其中对称运算是关于变量ξ1,…,ξi+j而不是关于η的。
下面给出拟微分算子的局部性概念。
定义1 函数a(ξ1,…,ξi,η)被称为局部的,如果在η→∞ 时,它关于η的展开式

中的所有系数 aj(ξ1,…,ξi)是变量 ξ1,…,ξi的对称多项式。
如果式(2)中所有的函数 aj(ξ1,…,ξj)(j=1,2,…)是局部的,则称式(2)是局部的。
定义2 拟微分算子
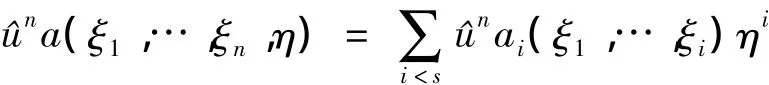
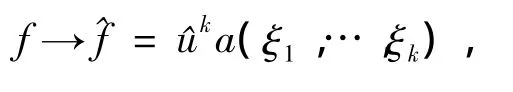
则Frechet导数f*的符号表示为
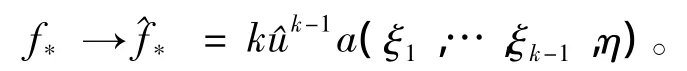
1.2 符号表示中的对称和近似对称
设F∈R+,研究形如

的方程,其中Δ(F)的符号表示为
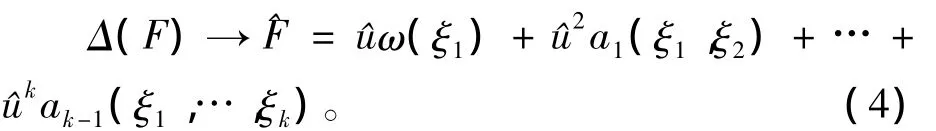
G=G1+ … +Gm,Gi∈,i=1,…,m。设Gi∈的符号表示为
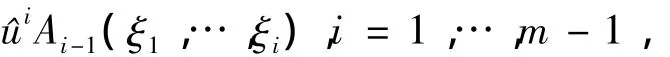
则G的符号表示为
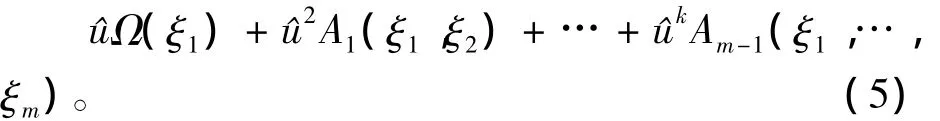
命题1 具有符号表示(4)的方程容许具有符号表示(5)的对称生成子的充分必要条件是式(5)中Ai满足如下条件
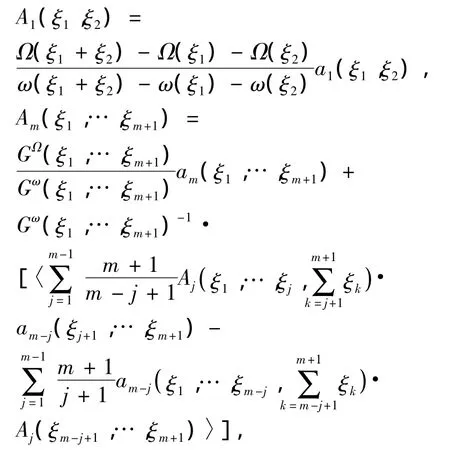
其中
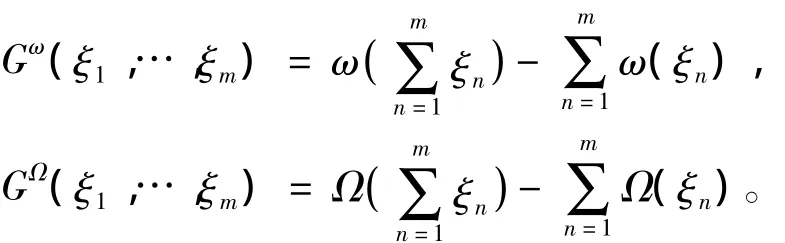
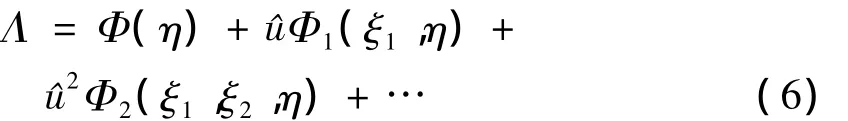
定义3 一个拟局部形式级数称为方程(3)的形式递归算子如果满足

定理1[10]如果方程(3)容许无穷多个高阶对称,则它具有形式递归算子(6),Φ(η)=η。
方程(7)的解还可以用函数 Φi(ξ1,…,ξi,η)表示。
命题2 设Φ(η)是任意函数且形式级数Λ = Φ(η)+(ξ1,η)+(ξ1,ξ2,η)+ …是方程(7)的解,则其系数Φm(ξ1,…,ξm,η)由如下递推公式确定
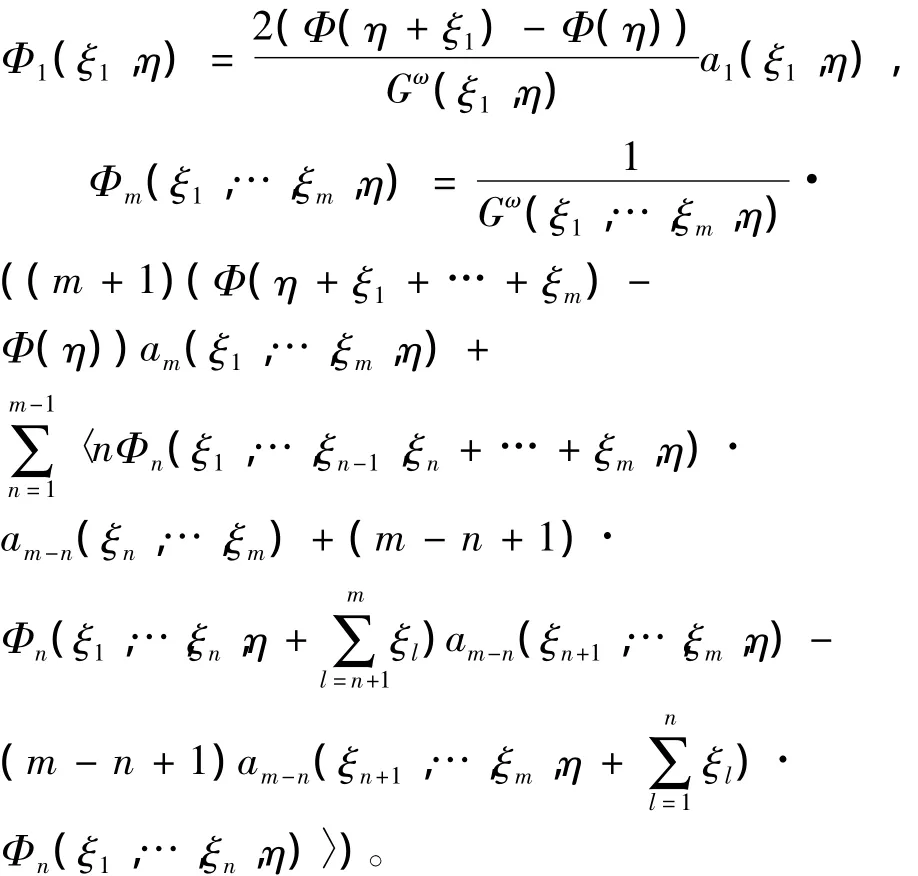
定理1和命题2表明方程(3)的可积性测试的步骤为:
1)计算方程(3)的符号表示并且计算首次系数 Φi(ξ1,…,ξi,η)(i=1,2,…);
2)检查拟局部性条件。
本文使用以上方法来推广可积Harry-Dym方程,得到推广的可积方程形式。
2 定理及其证明
本节给出关于Harry-Dym类方程(1)的可积性的以下结论。
定理2 若在c2,c5不全为零时方程(1)具有无穷多的拟局部高阶对称,则在尺度变换
x → αx,t→ βt,u → γu,
(其中α,β,γ为常数)的意义下,方程(1)必为下列方程之一
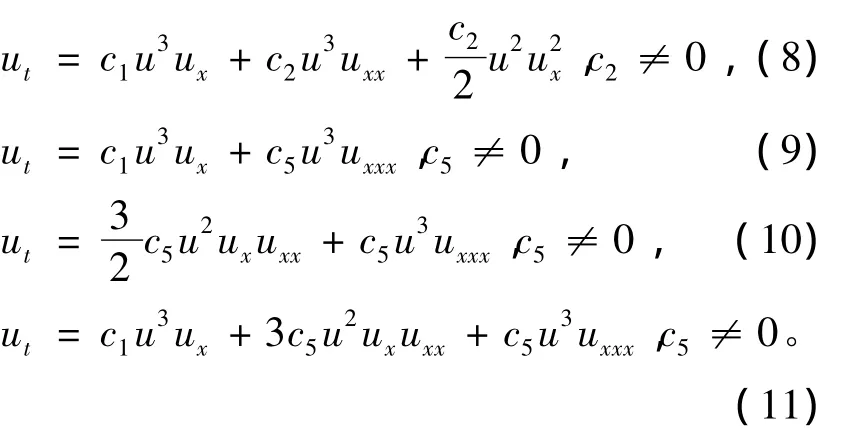
证 明 对u作平移变换u→u-1,可得新方程
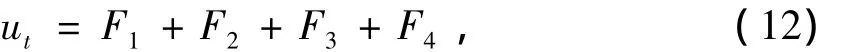
其中Fi为i次齐次多项式,即

下面由符号表示方法推导方程(12)的可积性条件。
1.由F1的符号表示为 ^u(- c1ξ1--可得:ω(ξ1)= - (c1ξ1++)。F2的符号表示为
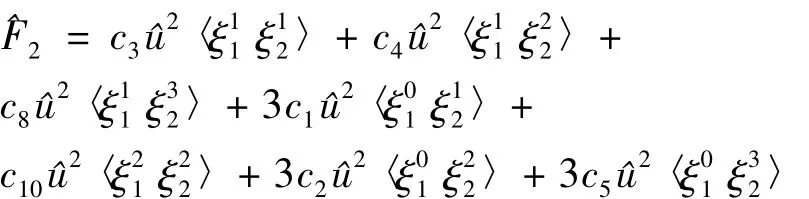
由定义

知
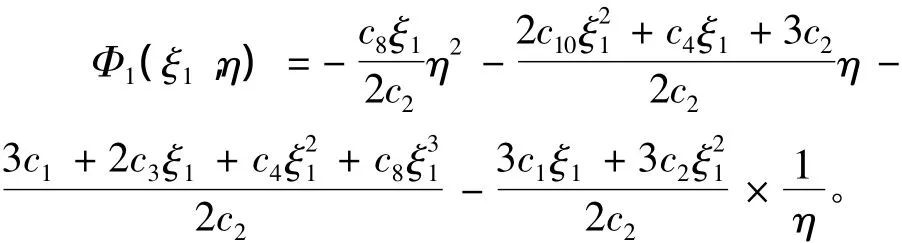
1)当c5=0时,上式表明Φ1可以表示为的形式,其中系数c(ξ1)是ξ1的多项式。
2)当c5≠0时,

其中Φ1n(ξ1)是ξ1的多项式。
综合以上两种情形可知,任何情形下Φ1(ξ1,η)是拟局部的。
2.F3的符号表示为
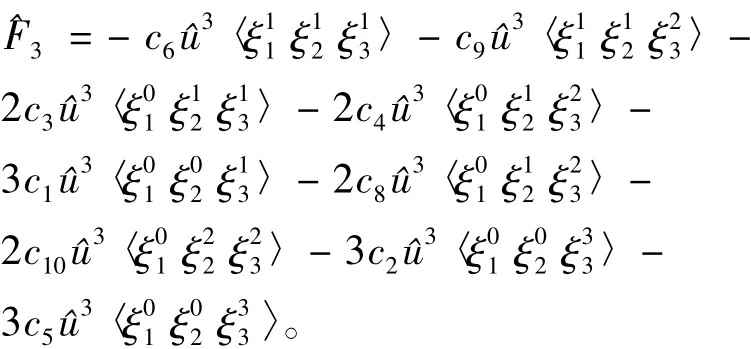
由定义可知
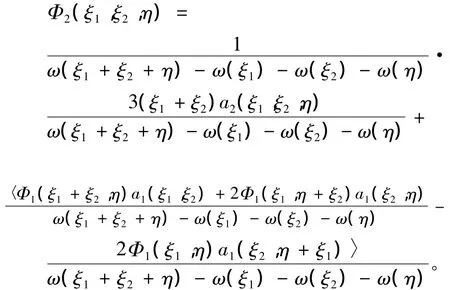
这里及下文中,由于Φi的形式复杂冗长,为简洁起见,我们略掉它们的具体表达式。
1)当c5=0,c2≠0时,要让Φ2是局部的即
其中 Φ2s是 ξ1,ξ2的多项式,必须有成立。
2)当c2=c3=0,c8=c10,c5≠0时,Φ2是局部的。
3.F4的符号表示为
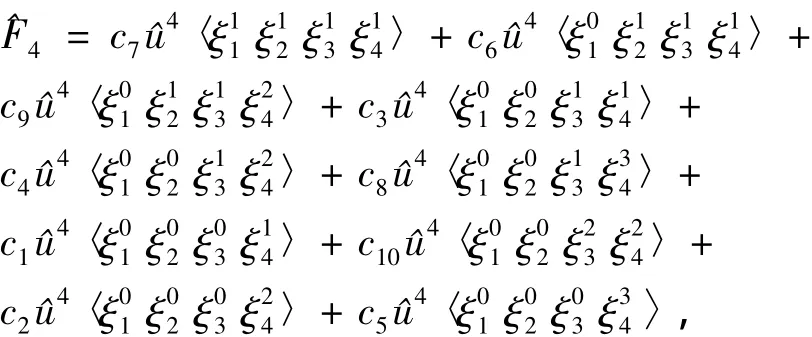
由定义可知

对于任意的ci,Φ3非常复杂。结合前面的讨论可知,要让方程(12)可积,只需讨论以下两种情形:
(3.1)当c2≠0,c3=时,要让Φ3是局部的,只要
c2≠0=c5=c6=c7=c8=c9=c10=0,此时方程为(8)。
(3.2)当 c2=c3=0,c8=c10,c5≠0 时,需分c9=0和c9≠0两种情况来讨论。
(3.2.1)当c9=0时,有以下几种情形:
1)c2=c3=c4=c6=c7=c8=c9=c10=0,c5≠0时,Φ3是局部的,此时得到方程(9),即为Harry-Dym方程。
2)c1=c2=c3=c6=c7=c8=c9=c10=时,Φ3是局部的,此时可得方程(10)。
3)c2=c3=c6=c7=c8=c9=c10=0,c5≠0,c4=3c5时,Φ3是局部的,此时可得方程(11)。
(3.2.2)当 c9≠0 且9=c2=c3=c6=c8=c10=0,时,要让Φ3是局部的,只有c2=c5=0成立,这与定理的题设c2,c5不全为零矛盾。故此种情形方程(12)不可积。
综合以上讨论,定理得证。
[1]KADANOFF L P.Exact solutions for the Saffman-Taylor problem with surface tension[J].Physical Review Letters,1990,65(24):2986-2988.
[2]NEWELL A C.Solitons in Mathematics and Physics[M].CBMS-NSF SIAM,1985:48.
[3]PALAIS R S.The symmetries of solitons[J].Bulletin of the American Mathematical Society,1997,34(4):339-403.
[4]WADATI M,ICHIKAWA Y H,SHIMIZU T.Cusp soliton of a new integrable nonlinear evolution equation[J].Progress of Theoretical Physics,1980,64:1959-1967.
[5]HEREMAN W,BANERJEE P P,CHATTERJEE M.Derivation and implicit solution of the Harry Dym equation and its connections with the Korteweg-de Vries equation[J].Journal of Physics.A:Mathematical and General,1989,22(3):241-255.
[6]MOKHTARI R.Exact solutions of the Harry-Dym equation[J].Communication in Theory Physics,2011,55:204-208.
[7]QIAO Zhi-jun.Commutator representations of nonlinear evolution equations:Harry-Dym and Kaup-Newell cases[J].Nonlinear Mathematical Physics,1995,2(2):151-157.
[8]GUO Ben-yu,ROGERS C.On Harry-Dym equation and its solution[J].Science in China(series A),1989,32(3):283-295.
[9]PEDRONI M,SCIACCA V,ZUBELLI J P.The Bi-Hamiltonian theory of the Harry-Dym equation[J].Theoretical and Mathematical physics, 2002, 133(2):1585-1597.
[10]MIKHAILOV A,NOVIKOV V S.Perturbative symmetry approach[J].Journal of Physics A:Mathematical and General,2002,35:4775-4790.
[11]NOVIKOV V.Generalizations of the Camassa-Holm equation[J].Journal of Physics A:Mathematical and Theoretical,2009,42(34):342002.

