谈大学数学教学中一题多解的意义

张雅轩

(中国民航大学理学院，天津 300300)

谈大学数学教学中一题多解的意义

张雅轩

(中国民航大学理学院，天津 300300)

本文针对数学例题，分别运用几何方法、代数方法和分析方法进行分析和求解，揭示不同方法之间的内在联系，体现数学分支的交叉融合.由此说明大学数学教学中一题多解的意义在于使学生更直观地认识到数学科学不同分支之间的内在联系和巧妙转化，深刻地领悟其中蕴含的数学思想，灵活地把握其中运用的数学方法，从而提高学生的数学能力.

一题多解；交叉融合；数学思想方法；教学意义

陈省身先生曾经说过：“学数学，最好的方法是做数学”.会用数学思想方法解决数学问题，能用多种方法来解决问题，无疑是“做数学”的一种能力.在数学教学中，恰当地使用一题多解，发挥一题多解的教学功能，有利于加深对于数学思想方法的理解，有利于提高运用数学思想方法解决问题的能力. 一般来说，来自同一种数学思想方法的多种解法比较容易得到.例如：在几何证明问题中添加辅助线的方法之下，由多种辅助线的添加方法产生的多解；在构造辅助函数证明有关命题的方法之下，由于辅助函数的不同而有了多种解法.同样，在换元法解决积分问题时，由多种不同的换元方法而产生多解；在用元素法解决问题时，因选定的微元对象不同，也产生多解.这样的例子还有很多.本文给出的例子略有不同，采用了几何的、代数的和分析的方法解决一个数学问题，这几种解法分属于数学的三大分支，即几何学、代数学和分析学. 以此为例，来解读这几种看似不相关的方法的内在联系，从数学方法、数学思想、数学分支的交叉融合等方面探讨这种类型一题多解题目的教学意义.

图1 画圆法思想

1 问题及其解法

题目：求椭圆5x2+8xy+5y2=9上的点到原点O的最长距离与最短距离.

1.1 几何方法——基于图形的几何特征

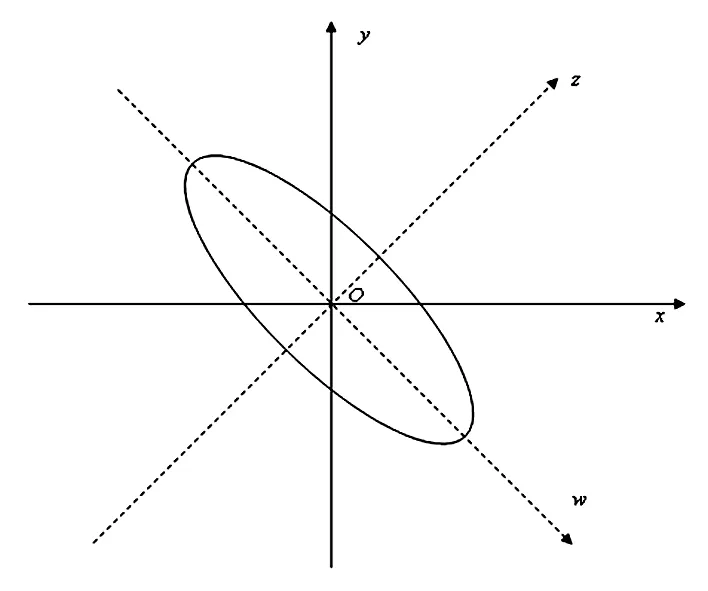
直观分析：因为题目中的椭圆方程不是标准方程，所以其长、短轴不在坐标轴上.但由于方程中不含一次项，所以该椭圆的中心位于坐标原点.很明显，如果点(x,y)在椭圆上，则点(-x,-y)也在椭圆上，因此原点是该椭圆的对称中心. 基于此，假设以原点为圆心画圆周，随着半径的逐渐增大，会先后出现两个与椭圆相切于两点的圆周.事实上，这两个圆周的半径就是本问题所求的最短距离与最长距离.而所有介于这两个圆周之间的圆周都与椭圆相交于4个点，其他的无数个圆周则与椭圆没有交点(图1).于是有了一种源于几何直观的解决方法.

1.1.1 画圆法

设以原点为圆心、r为半径的圆周方程为x2+y2=r2,r>0. 将其代入椭圆方程并消去y，得到64x4-64r2x2+(9-5r2)2=0. 利用求根公式可得

(1)

当r2<1或r2>9=1时，式(1)无意义，圆周与椭圆没有交点；当1

此方法从几何直观入手，运用初等数学的知识就能够解决问题.如果知道导数的几何意义以及隐函数的求导方法，还可进一步深入挖掘其几何特征，得到更简洁的解题思路.图1中椭圆上与原点距离最长和最短的点有一个共同特点，就是该点与原点的连线垂直于椭圆在该点处的切线.据此又有如下解法.

1.1.2 切线法

设椭圆上与原点距离最长或最短的点的坐标为(x0,y0)，则

农业生产水平和条件属于地区的社会经济特征。从理论上讲，干旱分区指标的构成不仅要反映自然条件因子的作用，还要反映社会因子的影响，而农业生产水平和条件相似的地区，将使得旱灾治理技术更能因地制宜地推动和发展，从而使研究结果更具实用性。

(2)

(3)

1.2 代数方法——基于代数学中的二次型理论

(4)

图2 正交变换解读椭圆位置

当椭圆方程中含有一次项时，上述诸方法便不再可行，但距离的最值问题依然存在，此时可考虑运用分析方法.

1.3 分析方法——基于分析学中的Lagrange乘数法

再换一个角度，本问题属于平面上两点间距离的最值问题.利用多元函数微分学的知识，一个直接的想法是将其转化为多元函数的条件极值问题，并用Lagrange乘数法[2]求解.方法是将平面上点与原点的距离作为目标函数，并将点的坐标满足椭圆方程作为约束条件，构造Lagrange函数.在具体实施时，为了方便求导，目标函数选取距离的平方.

构造Lagrange函数

F(x,y,λ)=x2+y2+λ(5x2+8xy+5y2-9),

解方程组

(5)

用于求解多元函数条件极值问题的Lagrange乘数法，它的适用范围很广.在本问题中，如果把椭圆方程换成含有一次项的非标准方程或者其他更加复杂的曲线方程，同样能够用Lagrange乘数法，在不确定图形的形状与位置的情况下进行求解，显示了该方法力量之强大.

2 一题多解的教学意义

在大学数学教学的某些环节中适当设计一题多解，能够让学生灵活地把握其中运用的数学方法，更深刻地领悟其中蕴含的数学思想，直观地认识数学科学不同分支之间的内在联系和巧妙转化，最终提高学生的数学能力，具有良好的教学效果和重要的教学意义.

2.1 从数学分支交叉融合的角度看

大学生已经接触到高等数学的知识与方法，具备了使用不同的数学内容相互沟通，利用它们的内在联系来思考问题的基本条件.但由于学生按照课程的分类分别学习数学分析、高等代数等课程，因此对于这些科目中知识的理解和掌握往往是彼此孤立的.建立功能良好的数学认知结构是十分必要的.在此情况下，恰当利用一题多解，运用几何的、代数的和分析的方法求解同一个数学问题，展示了数学三大核心领域——几何学、代数学、分析学——的思想方法及其内在关联[3].数学的各个分支之间不是孤立的，表面看似无关的知识却有着内在的联系，因此需要找出其间的联系，提取并有效整合相关的数学思想方法，与当前的数学问题建立关系.

2.2 从数学方法的角度看

数学方法的发展过程，是一个以高级替代低级的过程.高级的数学未必难，低级的数学未必容易[4].教师的职责，不仅是传授新知识，还要在教学中注重体现这一发展过程，引领学生以更“高级”的观点理解已有的知识，并将知识融会贯通，用于分析和解决具体问题.本文所述问题的第一种方法较为“低级”，直接从图形的几何特征出发；而后两种方法较为“高级”，分别用到了近代数学中的二次型理论和多元函数极值理论，不依赖于具体图形也能求解.前两种方法具有一定的局限性，对含有一次项的椭圆方程不适用；而第三种方法突破了这一局限，对任何椭圆方程甚至更加复杂的平面曲线方程都适用.本问题的讲授能够使学生直接体会到数学由低到高的发展过程，感受到“高级”的方法在分析解决问题时的优势.同时，通过引导学生运用二次型或多元函数极值这样的“高级”观点来理解题目中的几何事实，促使学生主动寻找新方法、运用新方法解决问题，潜移默化地建立起对数学发展过程的认识.

2.3 从数学思想的角度看

数学思想是数学学科的灵魂，是数学素养的重要组成部分，教师在大学数学教学的过程中更应注重对相关数学知识中数学思想方法的挖掘、渗透和生成[3].“数形结合”是朴素而重要的数学思想，大约在一万多年前人类就逐渐形成了“数”与“形”的概念，以及这两个概念之间辩证统一的矛盾关系.大量的数的关系都有其几何意义，如二次方程表示二次曲线；反之，一些几何量又可由数的关系表达出来，如切线的方向用导数表示.本文所述问题给出的二次方程就表示椭圆曲线，而第一种方法中所用的切线斜率依赖于导数的求解.把“数”与“形”的关系提示给学生，可以加深学生对“数形结合”数学思想的理解，使学生习惯于用数学思想思考新的问题.

2.4 从教学效用的角度看

一个问题往往涉及数学知识的多个方面，从不同的角度进行观察分析，可以引发不同数学知识的应用. 在数学教学中运用一题多解，不局限于形式和技巧的多变，而是使学生的思路更加开阔，在通法与特技之间，分清主次，有所取舍；在同一数学分支中的多技法与不同数学分支的多种方法之间，更多地着眼于后者，以期达到数学知识交叉融合、解题思路灵活多样、解题方法多种选择，而结果均殊途同归的效果，使学生加深对数学思想方法的理解，培养出对数学的浓厚兴趣和欣赏能力，最终提高数学能力.

3 一题多解教学中教师的作用

在一题多解教学中，教师的作用尤为重要.首先，教师要选取某些适当的教学环节设计适当的一题多解，这依赖于教师本人的数学积淀，以及在长期教学过程中的细心观察、日积月累和与同行的交流，不能一蹴而就.其次，教师要有意识地、潜移默化地引导学生从不同角度分析问题，用不同方法解决问题，并及时予以总结，启发学生领悟蕴含于分析求解过程中的种种深刻的数学思想及其内在联系.第三，教师要坚持在长期的教学过程中进行渗透，让学生充分掌握数学思想与方法，并运用它驾驭数学知识，培养数学能力，提高数学素养，最终形成自己的数学思维能力、推理分析能力、灵活运用知识的能力.

[1]北京大学数学系几何与代数教研室代数小组.高等代数[M].2版.北京:高等教育出版社,2002.

[2]陈传璋,金福临,朱学炎,等.数学分析(下册)[M].2版.北京:高等教育出版社,1999.

[3]王元明.数学是什么[M].南京:东南大学出版社,2003.

[4]龚昇.话说微积分[M].合肥:中国科学技术大学出版社,1998.

On the Importance of Multi-answer Problems in College Mathematics Teaching

ZHANG Ya-xuan

(College of Science, Civil Aviation University of China, Tianjin 300300, China)

In this paper we introduce a mathematical problem and present its geometrical, algebraic and analytic solving methods respectively. Then we reveal the inner relation between among methods and the cross amalgamation of different mathematical branches. This indicates the importance of multi-answer problems in college mathematics teaching. It provides students with the ability to transformation between mathematical branches vividly, to appreciate mathematical ideologies more deeply, and to understand the inner relation and use mathematical methods more flexibly. It eventually enhances the students’ mathematical ability.

multi-answer problem; cross amalgamation; mathematical ideology and methodology; teaching significance

2014-04-07

中国民航大学教研项目“基于CDIO和卓越班《线性代数》课程的教学改革探索与实践”。

张雅轩(1984- )，女，天津人，中国民航大学理学院讲师，博士，从事分布参数系统控制研究。

G642

A

2095-7602(2014)04-0139-04