基于含随机误差项蛛网模型的模拟仿真分析与决策

冯 林

安徽财经大学管理科学与工程学院，安徽蚌埠，233030

经典的蛛网模型［1］是在考虑时间因素的情况下，通过运用动态分析的方法，研究市场中那些生产周期较长的产品（如农产品、畜牧产品等）的供给、需求和价格之间的相互作用，以及分析各要素偏离均衡状态后的运动过程和结果的模型。蛛网模型的方程表示形式为：

模型的意思是说：商品的本期生产量Qst取决于商品上一期的价格Pt-1，而商品的本期需求量Qdt则只受本期价格Pt的影响，即由本期的市场实际价格所决定，当商品的供给量与需求量相等时，达到供需平衡的均衡状态，此时的价格即为市场均衡价格。其中，as、rs、ad和rd均为大于0的常数［2］。

虽然蛛网模型的提出是基于生产周期较长的商品，但实际上其理论适用于大多数商品的供需平衡分析。因为商品从生产到销售实现都有一定的时间间隔，虽然时间较短，但需求、供给和价格之间的作用原理与蛛网模型相同，厂商的生产量往往是通过以往的销售情况确定的，如果市场价格高、行情好，厂商就会扩大生产，供给量就会增加，当前价格就会相应降低，从而需求上升，如此往复。在该过程中，厂商的生产随着市场的波动而不断变化，会产生很多资源的浪费和错失很多机会，若能通过一定的方法模拟该过程，分析模拟结果，从中找出稳定的供需关系和均衡价格，就能为厂商的生产决策提供依据［3］。

1 含随机误差项蛛网模型构建

传统的蛛网模型认为供给量与需求量只取决于价格，而且是线性的，这本身就存在一定的缺陷。模型是对客观经济现象的抽象描述，模型中不可能包含所有的经济影响因素，而且复杂的经济现象中各要素之间的真实关系往往是非线性的，收集的数据也可能存在误差，另外，各种随机的意外事件也会经常影响到模型的准确性。因此，对蛛网模型引入误差项，其模型为：

将（4）式和（5）式带入（6）式得：

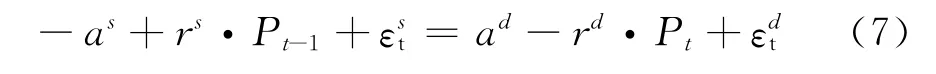
由此可以得到低t期的价格为：

将（10）代入（9）式得到本期的价格模型：

通过在模型中加入误差项，使得模型更具现实意义［6］。在实际的市场环境中，各要素不是唯一确定的，如以上分析所述，它们是在一定范围内波动的，价格可能因合作关系、人际关系、地域因素、预期因素等的不同而有所差异。因此，含误差项的蛛网模型与传统模型有所区别，供给与需求曲线已经不是一条曲线，而是一组曲线簇，通过图形表示结果如图1、图2、图3所示。

2 对模型进行模拟分析与决策

通过前面的理论分析和推导，得到了含随机误差项的蛛网模型，并在理论上阐释了模型可能出现的运动状态及其经济意义，而这种理论的分析是否符合于实际情况，这就要通过数据来对其进行验证。下面通过excel对模型进行数据模拟分析［7－9］。

模拟的模型是理论模型推导之后的具体模型，其形式为：

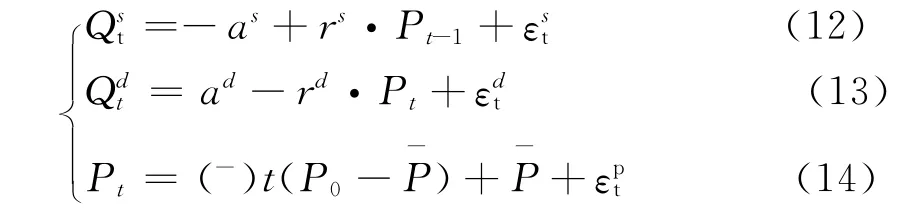
根据上述模拟模型，对其中的参数进行设置：ad都是均值为0的正态分布随机项，其方差分别为0．5、0．2和0．1，并且P0＝4 738，对该模型进行50期的模拟仿真，其结果如表1所示。

表1 收敛型模型模拟结果表

对表1中所得的价格数据进行分析，首先将所有数据进行平均，得其均值为4 761．513，方差为11．181 08。剔除第一项数据后的均值和方差分别为4 761．983和0．126 347；剔除前两项后为4 761．959和0．099 508；剔除前三项后为4 761．961和0．101 306；剔除前四项后为4 761．967和0．101 844。从中可以看出，价格在前几期波动较大，随后波动趋势放缓，接近于4 761．905（此数据为消除误差因素，将εst，εdt，εpt都设为0后模拟出的收敛价格，即传统模型下的均衡价格），波动幅度也稳定在0．1（等于价格的误差项εpt的方差）左右。由此得出，当rd＞rs时，价格随时间的增加而不断波动，且波动幅度越来越小，最后在误差范围内收敛于均衡价格，如图4所示。

图4 收敛型价格运动趋势图

在实际生产经营过程中，任何厂商在遇到价格急剧突增或突减时都会手足无措，不知如何决策才能既降低风险又保证收益。通过上述的模拟分析，得到了产品在未来的市场前景和状态，为生产经营者的决策提供了方向。在上述情况下，无论价格突增还是剧减，最终都会回到初始均衡状态。也就是说，当价格上升时，厂商不能盲目地扩大生产规模，造成资源和设备的浪费，而应看到造成这种情况的原因往往是供给量的减少，此时，厂商应该在保持原有生产的基础上，通过提高生产效率来增加产量，同时，可以在一定范围内提高价格，以获得较高的利润；若价格下降，则不必缩小规模，而应扩大规模，因价格终将恢复，所以厂商可以通过囤积产品或是兼并其他厂商，从而以最小的风险和代价获得市场的优势地位，实现企业的战略目标。

同样采用上述模型，对参数进行设置，更改参数rs＝2．1，其余参数不变，进行模拟，其部分结果如表2所示。

在实际中，需求量、供给量和价格不可能为负数，而在此处为了研究价格随时间的变化趋势，使其效果更明显，从而忽略该限制，但这并不影响结果的正确性。

表2 发散型模型模拟结果表

从以上数据中可以分析出，当rd＜rs时，价格会随着时间的增加而不断波动，且幅度越来越大，最终趋于无穷，呈现出发散状，如图5所示。

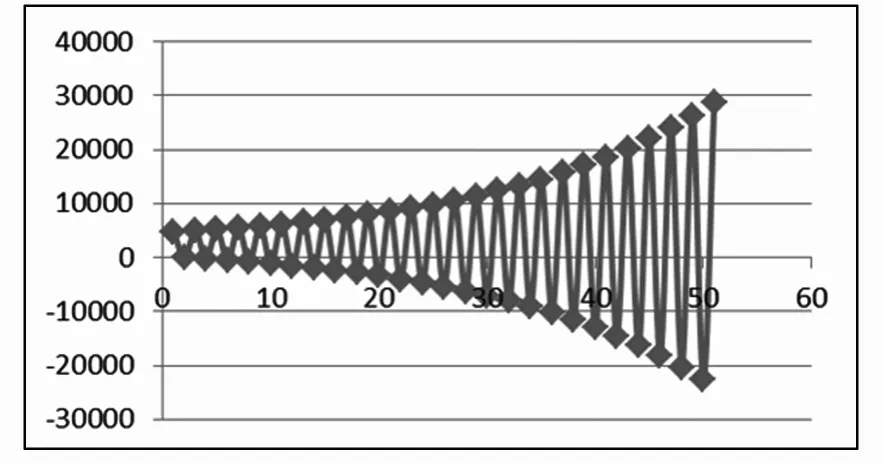
图5 发散型价格运动趋势图

这种情况下，价格波动幅度不断加大，对企业来说非常危险，此时，无论是生产者还是消费者对价格都非常敏感，往往是市场中出现了同类产品的替代品，对企业来说，最好的方法就是尽快转移重心，寻求新产品，并且尽量扩大产品宽度，分散风险。

同样采用相同的模型，对参数进行设置，更改参数rs＝2，使rd＝rs，其余参数不变，进行模拟，其部分模拟结果如表3所示。

从表3中的数据看，初期价格为4 738，间隔一期后为4 737．932，第4期为4 738．036，第6期为4 739．047，每间隔一期，价格就会回到初始价格附近，虽略有变化，但都在一定的误差范围内变动，并且通过计算得到初始值附近点的方差为0．009 034，约等于εpt，如此循环往复。为节省篇幅，此处并未将所有数据一一列出，但前几期的数据已经说明了价格变化规律，而且省去部分的数据也与上述数据所反映的趋势相同，如图6所示。由此得出，当rd＝rs时，价格随时间的增加呈周期性变化，都有回到初始状态的趋势，且始终在一定的误差范围内围绕初始 价格运动，整体上呈现出封闭状。

表3 封闭型模型模拟结果表

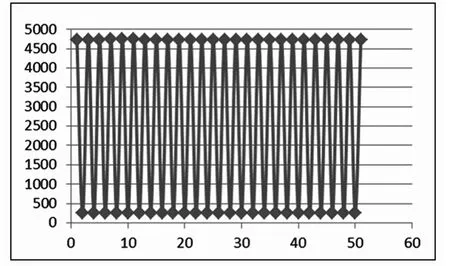
图6 封闭型价格运动趋势图

这种情况下，价格一旦偏离就不会回到初始的均衡状态，而是周期性的波动。如果生产者随着市场价格的上升而扩大生产，随着市场价格的下降而缩小规模，那将给企业造成巨大的机会损失和成本浪费，甚至可能因新建周期长、资金紧张、市场价格急剧下降等问题而使企业走向生存的边缘。虽然市场价格会大幅波动，但并没有像发散型那样不可控制，此时的市场往往是处于成熟期，厂商应该维持现有规模，并将价格风险转嫁给其他企业。例如，当价格上升时，可以在误差项范围内调整价格，以借助其他企业的生产力，实现自己虚拟扩张；当价格下降时，则可适当囤积产品。另外，在该情况下，企业往往也处于稳定状态，缺乏活力，所以应该进行适当的企业结构重组，增强企业的活力和生产效率，提高企业的创新精神，促进新产品的研发，从而避免价格陷阱，增强企业市场优势。

3 结束语

在传统蛛网模型中加入随机误差项，使得模型更加的灵活，更加符合现实要求，让分析结果更具可操作性。并且，通过对模型进行模拟分析，不仅证明了理论分析的正确性，而且体现了一定的预测功能，为生产企业确定发展方向和作出正确决策提供了依据。虽然本文在模型的收敛、分散、封闭三种情况下对企业的经营决策作了一一分析，但在实际的生产经营过程中，这三种情况并不是唯一出现、始终不变的，而往往是随时间交替影响的，因此，决策过程也不能一成不变，而应综合各种因素，随时调整策略。

［1］高鸿业．西方经济学：微观部分［M］．5版．北京：中国人民大学出版社，2010：48-51

［2］么海涛．蛛网模型的数学研究［J］．北京信息科技大学学报，2011（4）：96-98

［3］周三多，陈传明．管理学［M］．3版．北京：高等教育出版社，2010：97-108

［4］王楠，冯涛．蛛网模型的数学解析与实际应用研究［J］．大众科技，2010（1）：27-29

［5］庄华，任宁．蛛网模型的稳定性分析［J］．学术前沿，2005（12）：236-237

［6］陈伟．关于我国肉猪生产蛛网模型的修正［J］．中国物价，2007（10）：38-39

［7］鲁晓旭，张吉力．基于蛛网模型理论的柑橘生产和价格波动分析［J］．农村经济，2010（8）：60-62

［8］马宁，李尧．浅析蛛网模型在分析市场经济稳定条件中的应用［J］．商场现代化，2009（2）：182

［9］崔丽梅，龙勇．基于蛛网模型的花卉拍卖中价格与供应量波动研究［J］．安徽农业科学，2011，39（22）：13724-13730，13741