一种新的FH迭代学习控制器设计

李艳辉 张 畅 周秀杰

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

迭代学习控制(Iterative Learning Control，ILC)在给定时间内以简单的学习算法可以实现对期望轨迹的高精度跟踪，其基本原理是利用先前的控制信息不断修正控制输入，使系统跟踪性能随迭代次数逐步得到改善，且不依靠精确的数学模型，因而被广泛应用于机器人、航天控制及工业生产等领域[1～3]。在工程控制中，系统的复杂性、元器件的老化和对系统的简化处理，都会导致其数学模型不精确，从而直接影响控制效果，因此，考虑系统的不确定性是十分必要的。文献[4]利用鲁棒控制律处理系统中的不确定性，将鲁棒控制与ILC相结合，实现对被控系统的零误差跟踪。文献[5]分别针对常参数化、时变参数化的不确定性，利用类Lyapunov方法设计控制器，实现对误差轨迹的完全跟踪，然而，当系统存在扰动时，文献[4，5]的跟踪效果将会受到影响，甚至导致系统不稳定。

在实际生产过程中不可避免地存在各种外界干扰，这些干扰会大大降低系统的控制性能，因此，许多学者对如何抑制扰动进行了深入研究[6～9]。文献[6，7]分别提出带有衰减因子或时变遗忘因子的迭代学习控制算法，利用因子来减少扰动对控制量的影响。然而，这两种算法虽具有良好的控制效果，却没有考虑系统中不可预见的参数变化。文献[8，9]针对存在干扰的情况，分别设计了不同的高阶ILC控制器，并给出了其收敛条件，但系统的输出误差仍较大，跟踪效果不理想。

笔者针对存在初态误差、不确定性和干扰的情况，设计了非线性时变系统的新的FH ILC控制器。该控制器利用反馈控制克服不确定性和干扰的影响，同时利用ILC提高系统的跟踪性能，并采用λ-范数理论对提出的新的FH ILC算法进行收敛性证明。仿真实例表明在满足一定的收敛条件下，当系统的初态误差和输出干扰有界时，跟踪误差有界收敛，且该算法显著地提高了系统的跟踪精度和收敛速度，对干扰有较强的抑制能力。

1 问题描述①

考虑下列一类具有不确定性或干扰的重复非线性时变系统：

(1)

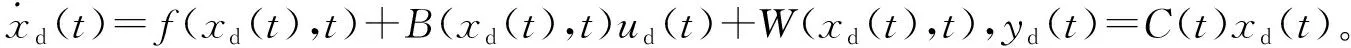
为不失一般性，假设该系统满足如下特性：

a. 存在R0∈Rm×r，使|I+R0C(t)B(xi(t),t)|≠0；

b. 初始误差有界，即‖xd(0)-xi(0)‖≤bx0,∀i。

笔者的目标是，在新的ILC控制器作用下，从任意有界的初始状态x0(t)开始，系统输出yi(t)在有限时间上能满意地跟踪上期望轨迹yd(t)。

为了证明新的FH迭代学习控制器的有效性，给出以下引理。

需要注意的是，初始状态通常设定成与期望值相同[9]，然而这种严格的初始定位条件在实际中是很难满足的。

为表达简便，以下公式的书写在没有歧义时省略时间变量t。

2 主要结果

考虑形如式(1)的系统，传统的高阶ILC方法跟踪误差较大，对干扰的抑制能力不强，而反馈控制在系统受到外部扰动和系统参数发生变化时，能够保证系统的鲁棒性，因此，笔者将反馈控制与ILC相结合，设计了具有如下形式的新的FH迭代学习控制器：

(2)

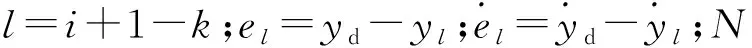
综合考虑反馈和前馈部分，则此控制器可表示为：

(3)

笔者针对具有不确定性和输出干扰的重复非线性系统(1)，提出一种如式(3)的新的FH ILC算法，下面采用λ范数论证此算法的收敛性。

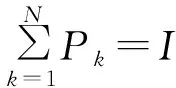
证明

为表达方便，做如下定义：

bC1sup‖C(t)‖,bC2

bx0‖δxl(0)‖，bV1

根据系统(1)和新的FH ILC算法(3)可得：

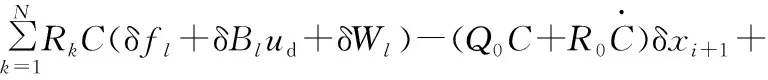
Q0Vi+1-R0C(δfi+1+δBi+1ud+δWi+1)+

利用Lipschitz条件，由上式可知：

d0+c0‖δxi+1‖}

(4)

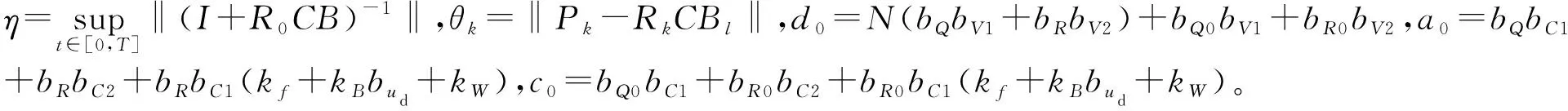
根据牛顿-莱布尼兹公式可知：

‖δxl‖=‖xd(t)-xl(t)‖

其中σ=kf+kBbud+kW。对上式两边取λ范数可得：

(5)

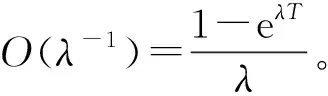
(6)

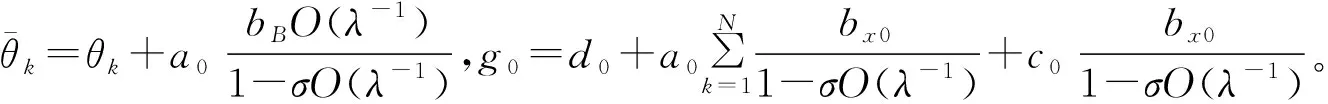
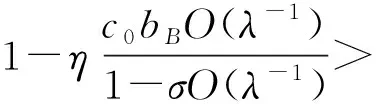
(7)

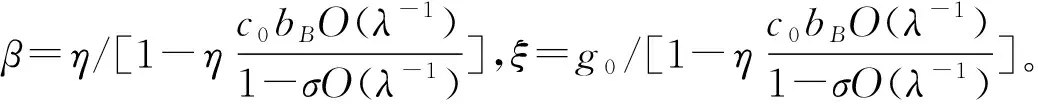
(8)

ei=δyi=yd-yi=Cxd-Cxi-Vi=Cδxi-Vi，进一步取λ范数可得：

‖ei‖λ≤bC1‖δxi‖λ+bV1

(9)

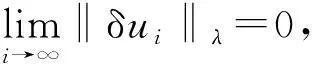
证毕。

需要注意的是，式(5)、(8)和(9)清楚地表明，对于任意ε>0，总存在正数δ，当干扰界bV1→ε时，‖ei‖λ→δ；当ε→0时，有δ→0，即输出干扰的界越小，控制精度越高，跟踪效果越理想。

在系统具有不确定性、初态误差个输出干扰的情况下，新的FH迭代学习控制器有效地提高了跟踪误差的收敛速度和控制精度，增强了对干扰的抑制能力。根据提出的控制律(3)，笔者归纳出新的FH ILC算法：

a. 置i=0，设定初始状态xi(0)和初始控制ui+1-k(t)，k=1,2,…,N,(t∈[0,T])，并存储期望轨迹yd(t)(t∈[0,T])；

b. 根据控制输入ui(t)(t∈[0,T]求出实际输出yi(t)(t∈[0,T]，并存储；

c. 计算跟踪误差ei(t)=yd(t)-yi(t)(t∈[0,T])，根据学习律(3)计算并存储新的控制输入ui+1(t)(t∈[0,T])；

d. 检验迭代停止条件，若满足条件则停止运行；否则执行步骤e；

e. 令i=i+1，返回步骤b。

3 仿真实例

考虑如下单关节机器臂非线性模型：

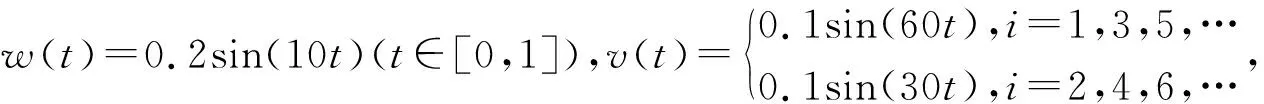
3.1 传统PD型高阶ILC

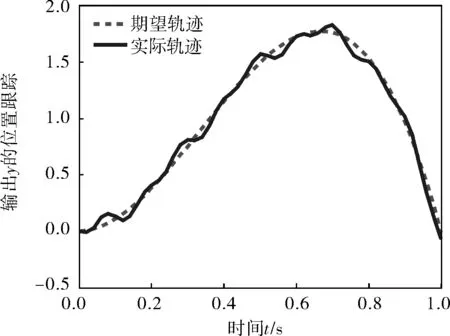
图1 第20次迭代关节位置响应

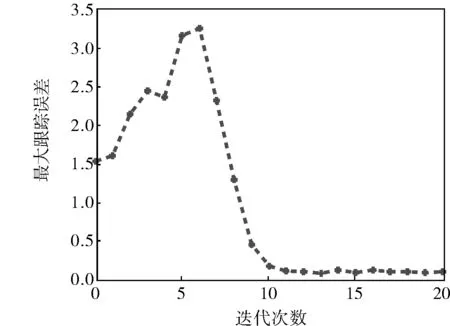
图2 跟踪误差响应过程

由图1、2可知，虽然实际轨迹和期望轨迹大致趋势相同，但由于扰动的影响，经过20次迭代后仍存在较大的波动；且跟踪误差在前几次迭代过程中出现阶段性增大的情况，经过15次迭代以后，跟踪误差降为0.1，跟踪精度不理想。

3.2 新的FH ILC

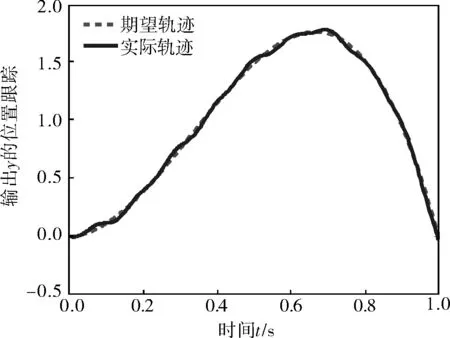
图3 第10次迭代关节位置响应

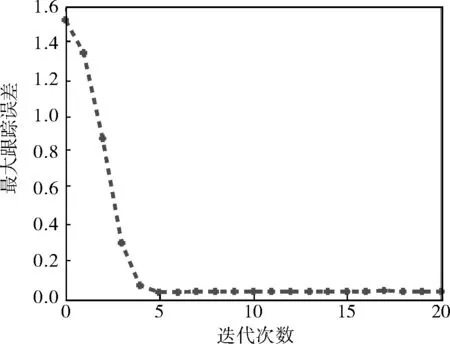
图4 跟踪误差响应过程

由图3、4可知，经过10次迭代后，新的FH ILC控制器实现了对期望轨迹的良好跟踪，且仅经过4次迭代，跟踪误差已约为0.05。与采用传统高阶ILC算法相比，采用新的FH ILC算法系统的跟踪精度和收敛速度得到有效提高，抗干扰能力得到明显增强。

4 结束语

给出一类重复非线性时变系统的新的FH ILC算法，通过引入反馈控制来补偿控制量以减小跟踪误差，从而消除不确定性和干扰的影响。在满足一定的收敛条件下，通过仿真实例表明了当系统的初始状态误差、系统输出干扰有界时，跟踪误差有界收敛，且该控制器能在较少的迭代次数内实现对期望轨迹的高精度跟踪，对干扰有较强的抑制能力。