软土场地大型LNG储罐考虑桩土相互作用的地震响应分析
刘 帅, 翁大根, 张瑞甫
(同济大学 土木工程防灾国家重点实验室,上海 200092)
LNG(液化天然气)是一种无色无味、无毒、无腐蚀性的优质高效能源,各国正逐步将其作为一种低排放量的清洁燃料加以推广。用以加工和存储液化天然气的储罐的建造量也因此不断增多,尤其是沿海的接收站LNG储罐项目正向着大型、超大型容量方向发展(最大可达20×104m3)。对于如此巨大而重要的结构物来说一旦在地震中发生破坏不仅会造成巨大的经济损失,而且会导致爆炸、火灾等灾难性后果,所以其抗震安全性能问题引起了国内外越来越多研究人员的重视。对储罐动力响应分析具有里程碑意义的研究是Housner[1]提出的刚性罐抗震分析理论,但实践证明该理论未考虑罐壁柔性,使得储罐的抗震安全性偏于非保守,所以之后的研究对罐壁的弹性进行了考虑。Edwards[2]首次采用有限元法对锚固储罐流固耦合地震响应进行了数值模拟研究;Haroun[3-4]采用有限单元法(罐壁和液面区域)和边界条件法(储液区域)相结合的计算方法将储液罐的流固耦合系统分解为相互独立的液壳系统和刚性罐对流系统进行分析。近年来,随着计算机技术的飞速发展,特别是一些大型通用有限元软件的出现,更是为储罐地震响应的数值模拟分析提供了很好的技术平台。Ozdemir等[5]在LS-DYNA中采用ALE(任意拉格朗日欧拉法)方法实现了非锚固罐考虑几何、材料非线性和土-罐接触非线性条件下储罐流固耦合地震响应的数值模拟,孙建刚等[6]在ADINA中建立了15×104m3立式储罐的三维实体有限元模型,探讨了浮顶质量、罐壁厚度等因素对储罐晃动频率和流固耦合频率的影响,张营[7]在ADINA中建立了16×104m3LNG全容罐的有限元模型,对比分析了加速度和位移加载条件下储罐的地震响应,李思[8]在ANSYS中对16×104m3LNG全容罐地震作用下的动力响应进行了分析,得出了最不利部位对储罐结构地震响应的影响。
虽然目前储罐的抗震研究工作已经取得了很多突破性进展,但多数都是基于刚性地基假定而进行的,对于考虑桩土相互作用对储罐地震响应影响方面的研究却不多见。在软土地区,大型LNG储罐通常采用均匀、对称的高桩基础形式来满足储罐底部散热条件及改善地基基础特性,高桩上端嵌固于罐体底板当中,下端埋置于半无限土体当中,当地震发生时,基岩波先是传经桩土地基后到达上部罐体,然后返回至地基当中,最终,在地基的辐射阻尼条件下逐渐消失。在整个过程当中,桩-土-罐相互作用相互影响,形成一个整体动力系统。如果在分析过程中假设地基为刚性体,直接对储罐输入自由场地表波激励,这将未能考虑桩-土-罐之间相互作用的影响,也未能进一步考虑场地类别、桩基布置形式及埋深等因素的影响。所以,为了确保大型LNG储罐的整体地震安全性,本文将利用大型通用有限元软件ANSYS建立起桩-土-LNG储罐的三维整体有限元模型,对考虑桩土相互作用对LNG储罐地震响应的影响进行分析,为工程实践提供参考。
1 储罐流固耦合有限单元法
1.1 基本力学方程
1.1.1 储液域
进行流体动力分析时基本假定:液体考虑为无粘滞性的、无旋的、不可压缩的理想流体。基本假定条件下理想流体在柱坐标系(r,θ,z)中应满足拉普拉斯方程[9]:
Δ2φ=0
(1)
其中φ(r,θ,z,t)是速度势,且有:
(2)
1.1.2 罐壁域
在罐壁区域任意一点应满足动力平衡微分方程(张量形式):
(3)
其中σij为罐壁应力分量,ui为罐壁位移分量,fi为罐壁体积力分量,ρs为罐壁质量密度。
1.1.3 边界条件
(1)在流体和罐壁的接触面上流体的径向速度和罐壁的径向速度应相等,则有:
(4)
其中wg和w分别为罐壁随地面一起运动(刚性脉冲)和自身弹性变形(柔性脉冲)的径向位移分量,R为罐壁半径。
(2) 流体自由表面由于扰动而发生晃动时,在重力的作用下总是趋向于恢复到静止的平衡位置(形成储液的对流晃动),所以在液体的自由表面(z=H)应满足自由面波条件(假设液体表面压力为0):
(5)
其中f为流体表面偏离平衡位置的垂直位移,g为重力加速度。
1.2 基于位移形式的流固耦合有限单元法
考虑到储液流体运动方程和弹性罐体运动方程的相似性,同样以流体位移为待求未知量,建立起流体基于位移的有限元格式,这样流体与罐体均为位移计算模式,可以方便进行标准有限元格式的计算,即便是复杂的耦合界面问题也能够较为容易地处理。采用流体和罐体的统一的基于位移的有限单元法后,储液罐流固耦合系统在地震作用下基于变分原理的整体动力有限元方程可以表示为:

(6)

由于理想流体几乎不存在抗剪强度,所以流体和固体仅在耦合界面的正法向发生相互作用,在切向上不存在剪力的传递。在采用有限单元法处理储液罐流固耦合问题时,应将流体与罐体在交界面处的法向节点位移约束,切向位移仍然保留。
2 土动力本构关系
土动力本构关系是了解在动力荷载作用下土体动力响应的基础,也是利用数值计算方法进行动力分析的前提条件。目前广泛采用的能够考虑土体非线性动力特性的计算模型大致有三种,一种是等效线性化模型[10],该模型简化了土的黏性和塑性能量损耗的复杂本质,将应力-应变关系用随动应变幅值变化的等效剪切模量与阻尼比来表示,而后通过多次计算,反复迭代获得近似的非线性解答;另一种是在非线性骨架曲线和Masing法则基础上发展起来的经验模型,例如Hardin-drnevich双曲线模型[11]、Martin-seed-davidenvic 模型[12]以及陈国兴等[13]提出的修正Davidenvic模型(在ABAQUS软件平台上成功地利用子程序开发实现了该模型),最后一种是利用一系列具有特定物理关系的物理元件按某种组合来构造总体应力-应变关系的模型,例如Iwan模型。在这三种模型当中,由于等效线性化方法在每次迭代计算中都属于弹性分析,不存在收敛问题,而且直观简单,所以在场地土层地震响应分析和土-结构相互作用分析时得到广泛应用,本文在进行桩-土-罐相互作用地震响应分析时采用了土的等效线性化模型,并在ANSYS软件平台上实现了该模型的算法。
3 边界条件
用有限单元法分析桩-土-罐动力相互作用时,需要从半无限地球介质中切取有限介质区域进行分析,在切取的边界上需建立人工边界以模拟连续介质的辐射阻尼,该辐射阻尼可以耗散从上部结构物反射过来的地震波能量。为减少人工边界波动反射带来的误差,国内外学者[14-15]做了许多有益的工作,其中最简单的处理方法是避开边界条件问题,直接采用自由边界,即取人工边界至结构物的距离足够远,以使在边界处波的衰减趋近于零。楼梦麟等[16]通过采用有限单元法分析了在水平地震波激振作用下均匀土层中有限土域的取值范围对计算精度的影响,结果得出确定有限土层合理取值范围的决定因素是长深比,当阻尼比为10%时,选取土层的长深比大于7之后,采用自由边界可以将计算结果与精确解的误差控制在5%以内。
4 桩-土-罐相互作用地震响应算例分析
4.1 罐体几何尺寸及材料属性
某LNG接收站项目工程采用特大型LNG全容罐,储罐的有效容积为16×104m3,外罐内径为82 m,外罐高49.9 m,壁厚上下均为0.8 m,外罐顶厚0.35 m,圆弧半径为40 m;内罐内径为80 m,内罐高35.43 m,储液高度为33 m,壁厚上下均为0.028 6 m;内外罐之间采用保温材料珍珠岩填充,厚度为1 m;混凝土底板的直径为86.6 m,厚度为1.2 m(中间0.9 m);采用摩擦型桩基础,桩长24 m,半径为0.6 m,共360根。特大型LNG储罐的断面示意图及桩基平面布置图如图1、2所示。
LNG储罐的材料属性见表1。

表1 LNG储罐材料属性

图1 LNG储罐断面图

图2 桩基平面布置图
4.2 场地条件及土的动力本构模型
由本工程《场地地震安全性评价报告》得知,该场地的等效剪切波速为56 m/s,小于150 m/s,且覆盖层厚度为100 m,大于80 m,判定为IV类软土场地。土体共分为7层, 各层土的密度和现场测得的土层剪切波速度如表2所示;由共振柱试验测得的动剪切模量比、阻尼比与动剪应变幅值的关系如图3所示。

表2 土层物理力学参数

图3 土剪切模量比和阻尼比与动剪应变幅值的关系
土的动力本构关系采用等效线性化模型,并利用有限元软件ANSYS 程序参数化设计语言(APDL)的功能将该模型在程序中实现。采用参数化编程实现该模型循环迭代的逻辑流程如图4所示。

图4 参数化语言实现等效线性化模型流程图
4.3 单元类型及有限元模型
有限元软件ANSYS拥有非常完善的单元库,针对不同的材料和分析类型,单元库提供了丰富的单元类型。依据桩土和储罐结构本身的特点,本文中桩-土-罐整体有限元模型所选用的单元类型如表3所示。
储液和内罐壁之间的相互作用是通过适当的耦合两个单元之间接触面上的节点来实现的,这就要求液体单元划分出来的节点应和内罐壁壳单元划分出来的节点相对应,而且此时还应将笛卡尔直角坐标系变换至柱坐标系下,变换后的X轴为圆周法向方向,Y轴为圆周切向方向,Z轴方向保持不变,然后在法向相同位置的节点进行耦合,保证储液不能与内罐壁分离,但在切向可以相对运动,并对内罐壁施加液动压力。液体单元和内罐壁壳单元之间的耦合作用如图5所示。

表3 有限元模型单元类型

图5 流固耦合作用示意图
用有限单元法分析桩-土-罐动力相互作用时所切取的有限土层的范围为半径750m的圆柱体,该范围满足自由边界长深比大于7的条件。鉴于桩土动力相互作用的复杂性,假设桩土之间不出现滑移和分离等相对位移现象,变形过程中桩土接触点的位移始终满足位移协调条件。由此建立起的桩-土-罐整体有限元模型如图6所示。

图6 桩-土-罐整体有限元模型
4.4 地震波选取
为了能够分析IV软土场地条件下考虑桩土相互作用对LNG储罐地震响应的影响,本文对以下两种模型状态进行了地震响应分析:
状态1(ST1):桩-土-罐相互作用分析模型(基岩地震动波输入)
在进行桩-土-罐相互作用地震响应分析时,依据《建筑抗震设计规范》[17]中I类场地(特征周期0.2 s)标准反应谱并通过傅里叶变换拟合了三条人工地震动时程,将其作为基岩地震动输入。原理上基岩地震动是从基岩顶面输入,而在有限元软件ANSYS中则是通过对桩-土-罐结构体系施加等价的外部激励来实现。为了考虑LNG储罐在SSE(安全停运地震)工况下的地震响应,将加速度峰值调整至0.3 g。其中一条归一化加速度时程曲线和其傅里叶谱如图7、8所示,3条地震波反应谱曲线如图9所示。

图7 PC1加速度时程曲线

图8 PC1加速度傅里叶谱

图9 归一化加速度反应谱(阻尼比5%)
状态2(ST2):假设地基为刚性的储罐分析模型ST2(自由场地表波输入,时程曲线如图10)。
地震波从基岩传至地表时,经过多次反射和折射,其频谱特征发生了很大的变化。图11给出了本文所选基岩地震动波在传经软土场地到达地表后其加速度反应谱变化情况,从图中可知,自由场地表波的长周期成分较基岩地震动波获得显著的增强。自由场地表波的特征周期在1s左右,这与Ⅳ类软土场地条件相符。

图10 PC1地表波加速度时程曲线

图11 地表波归一化加速度反应谱
4.5 计算结果与分析
在进行桩-土-罐相互作用地震响应分析之前,首先针对计算结构进行了模态分析,两种结构状态下模态分析结果的对比如表4所示。
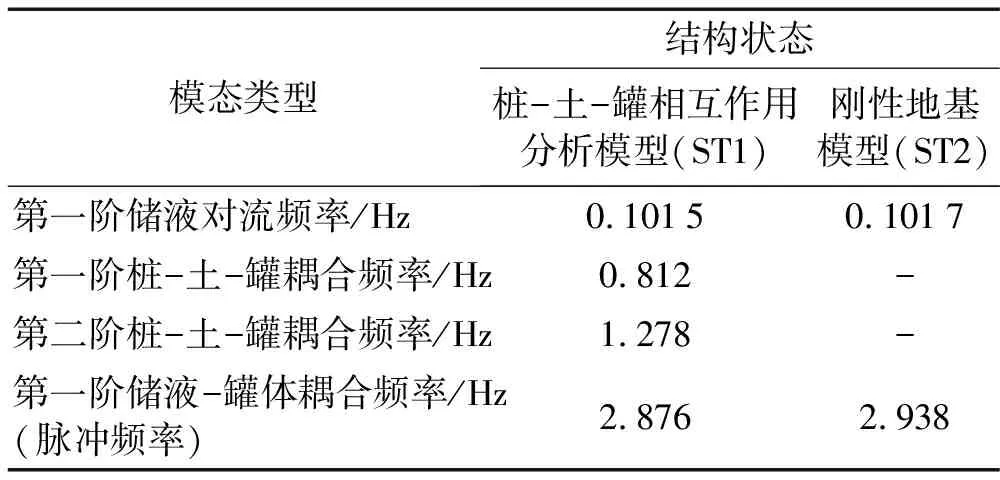
表4 模态分析结果对比
4.5.1 储罐基底剪力、倾覆力矩及晃动波高
IV类软土场地条件下考虑桩土相互作用时(ST1)和假设地基为刚性时(ST2),该LNG储罐在SSE工况下的基底剪力、倾覆力矩及晃动波高的时程曲线如图12所示,峰值和最大值如表5所示。
由表5可知,在IV类软土场地条件下考虑桩土相互作用以后,该LNG储罐的基底剪力和倾覆力矩的峰值分别减小了24%和7%;最大晃动波高增大了15%。
两种状态下储液的对流晃动形式相同,图13为在ST1状态下不同时刻储液对流晃动的云图。

图12 基底剪力、倾覆力矩及晃动波高时程曲线对比(PC1)

表5 基底剪力和倾覆力矩峰值及最大晃动波高对比

图13 储液对流晃动云图(5倍真实尺寸)
4.5.2 内罐壁等效应力
通过对比得知,两种状态下内罐壁Mises等效应力值的分布相似,即在地震作用方向均由一边向另一边逐渐增大,应力较大值也均出现在内罐壁与地震作用方向成零度角处,这和储液对流晃动的形式是一致的。图14为在ST1状态下不同时刻内罐壁Mises等效应力云图。

图15 内罐Mises应力峰值沿罐高分布
图15为在两种状态下内罐壁Mises等效应力峰值沿罐高的分布曲线(内罐壁与地震作用方向成零度角处)。从图中可知,内罐壁等效应力峰值先是在顶部较小,然后沿罐高向底部逐渐增大,直至接近罐底部位时出现内罐壁等效应力峰值最大值,然后又开始减小至罐底,峰值最大值均出现在离罐底约3 m处,未考虑桩土相互作用时为329 MPa,考虑桩土相互作用后有稍微减小,为323 MPa。由美国石油学会(API)标准可知,在低温状态下9%Ni钢的屈服应力达到515 MPa,所以在0.3 g地震作用下内罐均未出现屈服,不会发生破坏。
4.5.3 保温层对储罐地震响应的影响
内外罐之间采用珍珠岩保温材料填充,在数次循环荷载作用下保温材料会压缩变得密实,刚度也因此会增大,这将对内外罐之间的动力相互作用产生影响。为了分析这一影响,本文分别对保温材料弹性模量放大为5倍和10倍状态下罐体的动力响应进行了分析,分析结果如表6所示。
状态1(ST1):原结构;
状态3(ST3):5倍保温材料弹性模量;
状态4(ST4):10倍保温材料弹性模量。
由表6可知,相比于状态1,状态3条件下的基底剪力峰值减小0.6%,倾覆力矩峰值增大3%,最大晃动波高减小0.8%;状态4条件下的基底剪力峰值减小1.2%,倾覆力矩峰值增大4%,最大晃动波高减小0.8%,这说明随着保温层刚度在一定范围内的增加,基底剪力峰值、倾覆力矩峰值和最大晃动波高变化较小。

图16 内罐Mises应力峰值沿罐高分布

表6 基底剪力和倾覆力矩峰值及最大晃动波高对比
图16为三种状态下内罐壁Mises等效应力峰值沿罐高的分布曲线,由图可知,内罐壁等效应力峰值随着保温层刚度的增大有明显的减小,相比于状态1,状态3条件下内罐壁等效应力峰值最大值减小41%(189 MPa),状态4条件下内罐壁等效应力峰值最大值减小60%(129 MPa)。这说明随着保温层刚度在一定范围内的增加,内外罐之间的动力相互作用越来越明显,部分液动压力可以通过保温材料传递至外罐,由混凝土外罐来承担,对内罐起到了保护作用。
5 结 论
(1) 该LNG储罐的基底剪力和倾覆力矩峰值在IV类软土场地条件下考虑桩土相互作用以后分别有24%和7%的减小,故通常在以罐底基底剪力和力矩为控制条件进行储罐抗震设计时将地基视为刚体是偏于保守的。
(2) 虽然考虑桩土相互作用以后该LNG储罐基底剪力和力矩峰值均有减小,但其液面最大晃动波高却有15%的增大,这是储液的对流分量在IV类软土场地条件下考虑桩土相互作用以后被放大的结果。所以,对于波高比较敏感的LNG储罐在以基底剪力和力矩为控制条件进行抗震设计时应重视考虑桩土相互作用对波高的影响,否则将有可能造成储液的溢出或灌顶的破坏。
(3) 考虑桩土相互作用以后内罐壁Mises等效应力峰值最大值有稍微减小,且在两种状态下最大值均出现在离罐底约3 m处。
(4) 保温层对储罐的地震响应具有重要的影响,随着保温层刚度在一定范围内的增加,LNG储罐的基底剪力峰值、倾覆力矩峰值和最大晃动波高变化较小,但内罐壁等效应力峰值最大值减小明显,这对于防止罕遇地震作用下内罐底部发生屈曲破坏是有利的。
参 考 文 献
[1]Housner G W. Dynamic pressures on accelerated fluid containers [J]. Bulletin of the Seismological Society of America, 1957, 47(1):15-35.
[2]Edwards N W. A Procedure for dynamic analysis of thin walled cylindrical liquid storage tanks subjected to lateral ground motions[D].Michigan: University of Michigan-Ann Arbor, 1969.
[3]Haroun M A. Dynamic analysis of liquid storage tanks[R]. 1981010009051, Washington: National Science Foundation, 1980.
[4]Haroun M A. Vibration studies and tests of liquid storage tanks[J]. Earthquake Engineering and Structure Dynamics, 1983,11(2): 179-206.
[5]Ozdemir Z, Souli M, Fahjan Y M. Application of nonlinear fluid structure interaction methods to seismic analysis of anchored and unanchored tanks [J]. Engineering Structures, 2010, 32(2): 409-423.
[6]孙建刚,崔利富,赵长军,等. 15×104m3立式储罐隔震设计分析[J]. 地震工程与工程振动,2010, 30(4): 153-158.
SUN Jian-gang, CUI Li-fu, ZHAO Chang-jun, et al. Design and analysis of seismic isolation for 15×104m3vertical storage tank[J]. Journal of Earthquake Engineering and Engineering Vibration,2010, 30(4):153-158.
[7]张营. 大型全容式LNG储罐地震响应数值模拟研究[D]. 大庆:东北石油大学,2011.
[8]李思. 全容式LNG储罐的地震响应分析[D].天津:天津大学,2010.
[9]居荣初,曾心传. 弹性结构与液体的耦联振动理论[M]. 北京: 地震出版社, 1983.
[10]齐文浩, 薄景山. 土层地震反应等效线性化方法综述[J].世界地震工程, 2007, 23(4): 221-226.
QI Wen-hao, BO Jing-shan. Summarization on equivalent linear method of seismic responses for soil layers[J].World Earthquake Engineering, 2007, 23(4): 221-226.
[11]Hardin B O, Drnevich V P. Shear modulus and damping in soil: design equations and curves[J]. Journal of the Soil Mechanics and Foundation Engineering Division, ASCE, 1972, 98(7): 667-692.
[12]Martin P P, Seed H B. One dimensional dynamic ground response analysis[J]. Journal of Geotechnical Engineering, ASCE, 1982, 108(7): 935-952.
[13]陈国兴, 庄海洋. 基于Davidenkov 骨架曲线的土体动力本构关系及其参数研究[J]. 岩土工程学报, 2005, 27(8): 860-864.
CHEN Guo-xing, ZHUANG Hai-yang. Developed nonlinear dynamic constitutive relations of soils based on Davidenkov skeleton curve[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(8): 860-864.
[14]刘晶波, 谷音, 杜义欣. 一致粘弹性人工边界及粘弹性边界单元[J]. 岩土工程学报, 2006,28(9) :1070-1075.
LIU Jing-bo,GU Yin,DU Yi-xin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements[J]. Chinese Journal of Geotechnical Engineering, 2006, 28 (9) :1070-1075.
[15]Lysmer J, Kuhlemeyer R L. Finite dynamic model for infinite media[J]. Journal of the Engineering Mechanics, ASCE,1969,95(4):859-877.
[16]楼梦麟, 潘旦光, 范立础. 土层地震反应分析中侧向人工边界的影响[J]. 同济大学学报, 2003, 31(7):757-761.
LOU Meng-lin,PAN Dan-guang,FAN Li-chu. Effect of vertical artificial boundary on seismic response of soil layer[J].Journal of Tongji University, 2003, 31(7):757-761.
[17]GB50011-2010.建筑抗震设计规范[S]. 北京: 中国建筑工业出版社,2010.

