同轴对转行星齿轮传动系统动态特性分析
石万凯, 刘 敬, 龚建春
(1.重庆大学 机械传动国家重点实验室,重庆 400044; 2.攀枝花学院 机电工程学院,攀枝花 617000)
行星齿轮传动系统具有体积小、传动比大、承载能力强等优点。同轴对转传动系统不仅拥有普通行星齿轮传动的特点,还可以将单一输入转换成两个输出,实现减速增扭的作用。同时也可以满足在工作中产生较小的不平衡力矩和较低的振动噪声的要求。而行星齿轮系统的动力学分析对整个系统的振动噪声控制有很大影响,是同轴对转系统设计的主要内容之一。
20世纪70年代以来,国内外学者对行星齿轮机构动力学进行了许多理论与实验研究。Hidaka等[1]运用理论与实验相结合的方法,分析了行星齿轮传动中齿轮的安装与制造误差对系统载荷分配的影响,同时也得到了浮动某一构件能够改善系统的载荷分配。Kahraman等[2-3]用集中质量法建立了行星齿轮系统的非线性时变动态模型,在此模型中,考虑了销轴孔的位置误差与行星轮偏心误差对系统动态特性的影响,又通过实验模型验证了不同误差与行星轮个数对系统动态特性的影响。Lin等[4]建立了直齿行星齿轮传动系统的扭转—横向耦合模型,分析了无阻尼振动下系统的三种振动模式:扭转振动、横向振动和行星轮振动。孙智民等[5]建立了封闭行星齿轮传动系统的动力学模型,分析了差动级与封闭级的动载系数以及不同输入转速下太阳轮的浮动轨迹。陆俊华等[6]分析了不同装配误差与安装误差对2K-H型行星传动系统均载特性的影响。秦大同等[7-8]基于Lagrange方程建立了盾构机多级行星齿轮传动的动力学模型,分析该系统的模态特性、位移响应和加速度响应等。对于同轴对转轮系功率流流向,石万凯等[9-10]分析了由差动轮系和复合轮系组成的同轴对转轮系的功率流。并确定了其不产生功率循环所需要满足的条件。
1 齿轮传动系统的动力学模型
由定轴轮系与差动轮系组成的同轴对转传动系统如图1所示,定轴轮系由太阳轮Zs1、行星轮Zpi(i=1,2,…,N)和内齿圈Zr1组成,差动轮系由太阳轮Zs2、行星轮Zmj(j=1,2,…,M)、内齿圈Zr2以及行星架C组成,其中内齿圈是双齿圈且采用相同的几何参数。输入扭矩通过太阳轮分流传递给定轴轮系机构与差动轮系机构,并通过内齿圈和行星架C分别形成输出A和B。

图1 同轴对转传动系统简图
基于集中质量参数法建立同轴对转传动系统的动力学模型,模型中考虑各个齿轮副的时变啮合刚度、啮合阻尼和啮合误差的影响。图2(a)为固定坐标系下定轴轮系的动力学模型,其中Kspi、Cspi、espi分别为太阳轮Zs1与行星轮Zpi的啮合刚度、啮合阻尼和啮合误差,Krpi、Crpi、erpi分别为内齿圈Zr1与行星轮Zpi的啮合刚度、啮合阻尼和啮合误差;图2(b)是差动轮系以行星架转速ωc为动坐标的动力学模型,其中Ksmj、Csmj、esmj分别为太阳轮Zs2与行星轮Zr2的啮合刚度、啮合阻尼和啮合误差,Krmj、Crmj、ermj分别为内齿圈Zr2与行星轮Zmj的啮合刚度、啮合阻尼和啮合误差。在图(2)中,k1为太阳轮Zs1、Zs2之间的耦合扭转刚度,k2为内齿圈Zr1、Zr2之间的耦合扭转刚度,kC为行星架的扭转刚度,kr1、kr2分别为内齿圈Zr1、Zr2的支撑刚度,kp1、kp2分别为行星轮Zpi、Zmj的支撑刚度,行星轮支撑刚度的计算按Montestruc[11]提供的方法进行计算。

图2 同轴对转系统动力学模型
同轴对转传动系统共有(13+3N+3M)个自由度,其广义坐标如下:
X=(xs1,Hs1,Vs1,xpi,εpi,ηpi,xr1,Hr1,Vr1,xs2,Hs2,Vs2,xmj,εmj,ηmj,xr2,Hr2,Vr2,xc)T
(i=1,2,…,N;j=1,2,…,M)
(1)
式中:xs1,xpi,xr1,xs2,xmj和xr2分别为齿轮Zs1,Zpi,Zr1,Zs2,Zmj和Zr2沿啮合线的微位移,Hxy和Vxy(x=s,r;y=1,2)为齿轮xy中心的横向和纵向微位移,εpi和ηpi为行星轮Zpi中心的径向和切向微位移,εmj和ηmj为行星轮Zmj在动坐标系下质心的径向和切向微位移,xC为行星架C在其半径rC上的切向微位移。
2 同轴对转系统的动力学平衡方程
设δs1pi和δr1pi为定轴轮系第i个行星轮与太阳轮和内齿圈沿啮合线的等效微位移,δs2mj和δr2mj为差动轮系第j个行星轮与太阳轮和内齿圈沿啮合线的等效微位移,则:
(2)
式中,φi=2π(i-1)/N为定轴轮系第i个行星轮相对于第一个行星轮的位置角,φj=2π(j-1)/M为差动轮系第j个行星轮相对于第一个行星轮的位置角;espi和erpi分别为定轴轮系行星轮与太阳轮和内齿圈的等效啮合误差,esmj和ermj分别为差动轮系行星轮与太阳轮和内齿圈的等效啮合误差;α1和α2分别为定轴轮系行星轮与太阳轮和内齿圈的啮合角,α3和α4分别为差动轮系行星轮与太阳轮和内齿圈的啮合角。
根据式(2)中的微小位移量,乘以啮合刚度可以得到每对齿轮副之间的啮合力。令Fs1pi和Fr1pi为定轴轮系行星轮与太阳轮和内齿圈的啮合力,Fs2mj和Fr2mj为差动轮系行星轮与太阳轮和内齿圈的啮合力,则各个齿轮副沿啮合线方向的啮合力为:
(3)
同理可以得到齿轮副的啮合阻尼力,令Ds2pi和Dr2pi为定轴轮系行星轮与太阳轮和内齿圈的啮合阻尼力,Ds2mj和Dr2mj为差动轮系行星轮与太阳轮和内齿圈的啮合阻尼力,则各个齿轮副沿啮合线方向的啮合阻尼力为:
(4)
根据Lagrange方程推导出同轴对转系统各个自由度的振动微分方程:
定轴轮系太阳轮平衡方程:
定轴轮系行星轮平衡方程:
(5b)
定轴轮系内齿圈平衡方程:

(5c)
差动轮系太阳轮平衡方程:
(5d)
差动轮系行星轮平衡方程:
(5e)
差动轮系内齿圈平衡方程:

(5f)
差动轮系行星架平衡方程:
(5g)
式中M和m分别为各个构件的等效质量和平移质量,且M=J/r2,J为构件的转动惯量,对于齿轮,r是其基圆半径rb,对于行星架,r是其当量基圆半径rbc。T1为同轴对转系统输入扭矩,T2为差动轮系内齿圈Zr2的输出扭矩,T3为差动轮系行星架C输出扭矩。
将方程(5a)~(5g)整理成如下的矩阵形式:

(6)
式中:M,X为广义质量矩阵,广义坐标位移列阵;C,F为阻尼矩阵,外载荷列阵;K(t)为时变刚度矩阵。
3 系统的激励与功率流
3.1 综合啮合误差激励
齿轮的制造误差和安装误差是齿轮传动系统产生振动的主要因素。误差可以用随齿轮啮合周期变化的正弦函数来描述,并且认为行星架安装和制造偏心误差都包含在太阳轮和齿圈的偏心误差中,只用考虑齿轮偏心误差的影响即可[5]。
将定轴轮系偏心误差与齿频误差等效到齿轮副啮合线上,则:

(7)
式中,Es1pi和Er1pi分别表示行星轮与太阳轮和内齿圈啮合的齿频误差,其初相位分别为βs1pi和βr1pi;Es1,Epi和Er1分别表示太阳轮、行星轮和内齿圈的偏心误差,其初相位分别为βs1,βpi和βr2;ω1表示定轴轮系的啮合齿频,ωs1,ωpi和ωr1分别表示太阳轮、行星轮和内齿圈的角速度。
将差动轮系偏心误差与齿频误差等效到齿轮副啮合线上,则:

(8)
式中,Es2mj和Er2mj分别表示行星轮与太阳轮和内齿圈啮合的齿频误差,其初相位分别为βs2mj和βr2mj;Es2,Emj和Er2分别表示太阳轮、行星轮和内齿圈的偏心误差,其初相位分别为βs2,βmj和βr2;ω2表示差动轮系的啮合齿频,ωs2C,ωmjC和ωr2C分别表示太阳轮、行星轮和内齿圈相对行星架的角速度。
3.2 时变啮合刚度激励
本文齿轮时变啮合刚度的计算按Maatar等[11]推导的公式进行计算,则:

(9)
式中,τ=t/Tm,t为时间,Tm为啮合周期;b齿宽,ε为直齿轮副重合度,k0为静载荷下单位齿宽平均啮合刚度,且:
Ak=sin(2πkε)/(π·ε·k)
Bk=(1-cos(2πkε)/(π·ε·k)
3.3 功率流分析
对于图1所示的同轴对转传动系统,通过合理的齿数配比可以满足ω2=-ω2的设计要求,同时在给定的输入功率条件下,此传动系统可能存在功率循环的问题,影响传动的效率。同轴对转传动系统不存在功率循环且定轴轮系也传递功率的条件是[9]:
(10)
式中:i为设计传动比,且i=ωs1/ωr1。
对于此同轴对转传动系统,还需满足|T2|≅|T3|,可以得到:
(11)
式中:P1为定轴轮系分流的功率,P2为差动轮系分流的功率,P为同轴对转系统输入功率。
4 系统微分方程求解及动态特性分析
对于微分方程组,得到其解析解是非常困难的,一般采用数值分析方法进行求解,本文采用4阶Runge-Kutta法来获得方程(6)的数值解。对某一同轴对转系统运用上述方法进行数值计算,其主要参数如下,两级太阳轮与行星轮精度等级为5级,内齿圈为6级。定轴轮系:Zs1=22,Zpi=44,Zr1=110,模数m1=1.75,齿宽b1=20 mm,行星轮个数N=3;差动轮系:Zs2=55,Zmj=27,Zr2=110,模数m2=1.75,齿宽b2=30 mm,行星轮个数M=3;系统输入转速n=10 000 r/min,输入功率P=300 kW,各齿轮的偏心误差为10 μm,齿频误差为5 μm。
4.1 同轴对转系统各构件振动响应
由于定轴轮系与差动轮系中的各个行星轮只存在空间位置差,并且在本文中各个行星轮综合误差取相同值,所以在每一级中只对其中一个行星轮进行振动分析。各级太阳轮和行星轮的振动位移时域曲线如图3、图4和图5 所示。各个齿轮的振动位移曲线都是关于y=0轴对称,并且呈现出低频周期性波动;由于差动轮系承担了5/6的输入扭矩,且啮合频率更高,其扭转振动幅值高于定轴轮系;同时也可以看出,差动轮系太阳轮采用了浮动装置,横向和纵向的振动位移相对于其扭转振动来说,振动位移曲线更加的平滑。
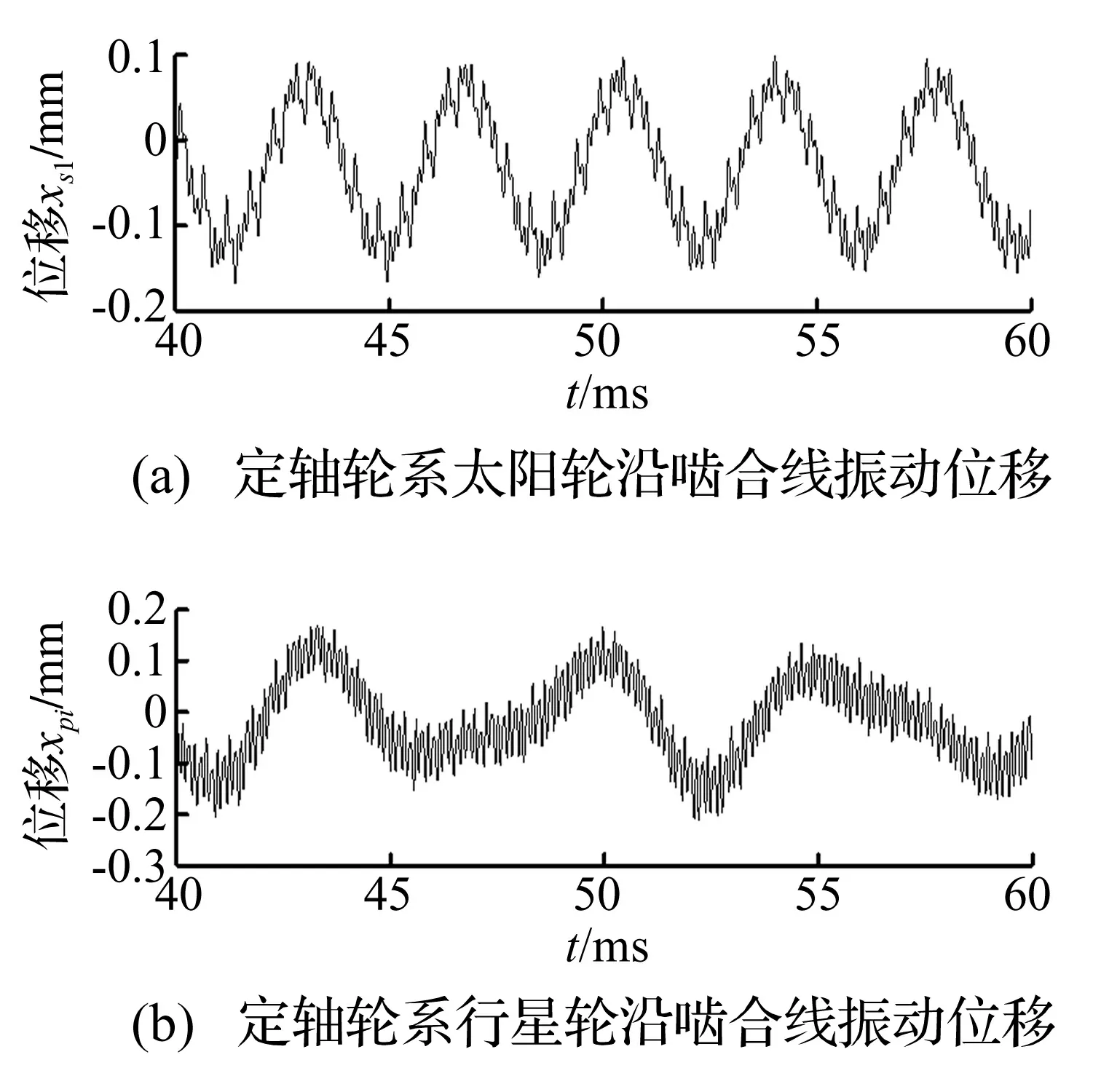
图3 定轴轮系位移动态响应曲线
系统部分构件速度动态响应如图6和图7所示。
由图6、 7可知,定轴级与差动级的太阳轮和行星轮沿啮合线的振动速度响应规律相同,总是关于y=0对称,并且不具有周期性,两级太阳轮的输入转速相等,但外部激励不同,速度响应曲线相似,幅值不等,定轴级太阳轮振动速度幅值约为1.4 m/s,差动级约为3.8 m/s。同时,行星架的扭转振动呈现出周期性,但振动速度幅值较小,约为0.8 m/s,主要是因为行星架转动惯量较大。

图4 差动轮系太阳轮位移动态响应曲线

图5 差动轮系行星轮位移动态响应曲线

图6 定轴轮系扭转速度动态响应曲线

图7 差动轮系扭转速度动态响应曲线
4.2 系统的均载特性
行星齿轮传动由于受各个齿轮偏心误差与齿频误差的影响,每个行星轮承担的载荷并不相等,通常用均载系数来表示,同时构件是否浮动也对载荷分配有影响。均载系数越大,行星齿轮系统的载荷分配越不均匀。将式(6)中得到的位移响应代到式(3)中,得到弹性啮合力Fs1pi,Fr1pi,Fs2mj和Fr2mj。令bspik1和bspik2分别为定轴轮系的在一个啮频周期内外啮合与内啮合的均载系数,bsmjk1和brmjk2分别为差动轮系的在一个啮频周期内外啮合与内啮合的均载系数,则
(12)
式中:k1=1,2,…,n1;k2=1,2,…,n2,n1和n2分别为同轴对转轮系定轴级与差动级的啮频周期数。
由于定轴级或差动级中行星轮的内啮合与外啮合均载系数基本相等,因此本文中只比较定轴级和差动级行星轮与太阳轮啮合的均载系数。由图8和图9可知,两级均载系数呈现周期性波动,且定轴级的波动幅值大于差动级。定轴级的均载系数约为1.02,差动级的均载系数约为1.01,差动级比定轴级载荷分配更均匀。同时可以看出,在每对齿轮副偏心误差和齿频误差取相等的条件下,定轴轮系比差动轮系的载荷分配更加敏感。

图8 定轴轮系外啮合各行星轮的均载系数

图9 差动轮系外啮合各行星轮的均载系数
5 结 论
(1) 基于Lagrange方程采用集中参数法建立了同轴对转传动系统的动力学方程,考虑了误差激励、刚度激励和功率流对系统的影响,运用数值分析方法求解了同轴对转传动系统各个构件的动态响应。
(2) 同轴对转系统各个构件的动态响应规律相似,但幅值大小不等。差动轮系各个构件沿啮合线的位移响应和速度响应幅值都要高于定轴轮系,这是因为差动轮系啮合齿频高,且分流了更多的功率。
(3) 定轴轮系的均载系数高于差动轮系,载荷分配更加不均匀。在相等的误差激励下,定轴轮系与差动轮系相比,误差的敏感性更高。
参 考 文 献
[1]Hidaka T, Sugimoto N, Ishida T. Effects of errors of elements on load distribution in planetary gears with various load equalizing mechanisms[J]. Japanese Mechanical Academic Society Collection, 1986, 52(480): 2200-2206.
[2]Kahraman A. Load sharing characteristics of planetary transmissions[J]. Mechanisms and Machine Theory, 1994, 29(8):1151-1165.
[3]Kahraman A. Static load sharing characteristics of transmission planetary gear sets: model and experiment[J]. SAE Transactions, 1999, 108(2): 1954-1963.
[4]Lin Jin, Parker R G. Analytical characterization of the unique properties of planetary gear free vibration [J]. Journal of Vibration and Acoustics, 1999, 121(3) :316-321.
[5]孙智民,沈允文,李素有. 封闭行星齿轮传动系统的动态特性研究[J]. 机械工程学报,2002,38(2):44-48.
SUN Zhi-min, SHEN Yun-wen, LI Su-you. Study on dynamic behavior of encased differential gear train [J]. Chinese Journal of Mechanical Engineering, 2002,38(2):44-48.
[6]陆俊华,朱如鹏,靳广虎. 行星传动动态均载特性分析[J]. 机械工程学报,2009, 45(5):85-90.
LU Jun-hua, ZHU Ru-peng, JIN Guang-hu. Analysis of dynamic load sharing behavior in planetary gearing[J]. Chinese Journal of Mechanical Engineering, 2009, 45(5):85-90.
[7]秦大同,肖正明,王建宏. 基于啮合相位分析的盾构机减速器多级行星齿轮传动动力学特性[J]. 机械工程学报,2011,47(23):20-29.
QIN Da-tong , XIAO Zheng-ming, WANG Jian-hong. Dynamic characteristics of multi-stage planetary gears of Shield Tunneling Machine based on planet mesh phasing analysis[J]. Chinese Journal of Mechanical Engineering, 2011,47(23):20-29.
[8]秦大同,肖正明,王建宏,等. 盾构机主减速器三级行星传动系统扭转动力学[J]. 中国机械工程,2010,21(18): 2176-2182.
QIN Da-tong , XIAO Zheng-ming, WANG Jian-hong , et al. Study on torsional dynamics of 3-stage planetary gears of main reducer used in driving cutter head of Shield Tunneling Machine. China Mechanical Engineering, 2010, 21(18):2176-2182.
[9]石万凯,张庆伟,秦大同. 同轴对转减速机构功率流分析[J]. 农业机械学报,2008, 39(5):165-168.
SHI Wan-kai, ZHANG Qing-wei, QIN Da-tong. Analysis on power flow of co-axial counter rotating reducer[J]. Transactions of the Chinese Society for Agricultural Machinery. 2008, 39(5):165-168.
[10]Shi Wankai, Li Liangjun, Qin Datong, et al. Analysis of power flow in a counter-rotating epicyclic gearing for electrical propulsion system[J].Journal of Mechanical Engineering Science, 2011, 225(12):2973-2980.
[11]Montestruc A N. Influence of planet pin stiffness on load sharing in planetary gear drives[J]. Journal of Mechanical Design, 2011, 133(1): 014501.
[12]Maatar M, Velex P. An analytical expression for the time-varying contact length in perfect cylindrical gears: Some possible applications in gear dynamics [J]. Journal of Mechanical Design, 1996, 118(12):586-589.
[13]李润方,王建军. 齿轮系统动力学[M]. 北京:科学出版社,1996.

