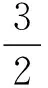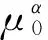连续函数的Altman型不动点定理*

李楚玲，许绍元

(韩山师范学院数学与统计学系，广东 潮州 521041)

连续函数的Altman型不动点定理*

李楚玲，许绍元

(韩山师范学院数学与统计学系，广东 潮州 521041)

由闭区间上连续函数的性质得到闭区间上连续函数的一个基本不动点定理，从而推出连续函数的Altman型不动点定理.

连续函数；不动点定理；根的存在性定理

连续函数是微积分学的最基本也是最重要的研究对象.闭区间上连续函数的性质定理(包括最大最小值定理、介值性定理)以及微分中值定理(包括罗尔定理、拉格朗日中值定理和柯西中值定理)，它们构成了微积分学的理论基础，也是研究函数的有力工具，在微积分学中具有广泛的应用.

近年来，人们对Altman型不动点定理的研究产生浓厚的兴趣.文献[1-11]研究了Banach空间中几类非线性算子，借助Leray-Schauder拓扑度理论，得到若干Altman型不动点定理.笔者就连续函数的Altman型不动点存在的问题作进一步讨论.在此，并不需要深奥的拓扑度理论，只需要运用闭区间上连续函数的根的存在性定理，就可以得到闭区间上连续函数一系列新的Altman型不动点定理.

1 预备知识

首先介绍闭区间上连续函数不动点的定义.

定义1[12]设f(x)是闭区间[a,b]上的连续函数，即f:[a,b]→R，若存在一点c，使得f(c)=c，则称c是f(x)在闭区间[a,b]上的不动点.

图1 根的存在性定理的几何意义

下面给出闭区间上连续函数的根的存在性定理.

定理1[12]若函数f(x)在闭区间[a,b]上连续，且f(a)与f(b)异号，则至少存在一点x0∈(a,b)，使得f(x0)=0，即方程f(x)=0在(a,b)上至少有1个根.

图1描述了闭区间上连续函数的根的存在性定理的几何意义.

首先利用闭区间上连续函数的根的存在性定理，建立闭区间上连续函数的一个基本不动点定理，然后在适当的边界条件下，得到闭区间上连续函数的若干不动点定理.

2 主要结果及证明

首先，给出闭区间上连续函数的一个基本不动点定理.

引理1 设f(x)是闭区间[a,b]上的连续函数，a<0

f(x)≠λx,

(1)

则f(x)在(a,b)上至少有1个不动点.

证明由(1)式,当x=a时,f(a)≠λa,∀λ≥1成立,故f(a)>a,否则f(a)≤a,于是存在λ≥1，使得f(a)=λa，这与f(x)≠λx矛盾.所以f(a)>a，即f(a)-a>0.

当x=b时,f(b)≠λb,∀λ≥1,b>0成立,故f(b)

图2 Leray-Schauder不动点定理的几何意义

设函数g(x)=f(x)-x,x∈[a,b]，因f(x)是[a,b]上的连续函数，故g(x)也是[a,b]上的连续函数，且有g(a)=f(a)-a>0，g(b)=f(b)-b<0，有g(a)g(b)<0.由根的存在性定理，至少存在一点ξ∈(a,b)，有g(ξ)=0，即f(ξ)-ξ=0，故f(ξ)=ξ.所以f(x)在(a,b)上必有不动点.

图2表示引理1的几何意义.它说明连续函数f(x)的图像必经过直线y=x，即与直线y=x至少有1个交点.

由引理1可以得到一系列连续函数的Altman型不动点定理.

定理2 设f(x)是闭区间[a,b] 上的连续函数，a<0

|f(x)-x|α|x|β≥|f(x)|α|f(x)+x|β-|f(x)|α|x|β∀x∈{a,b}

(2)

成立，则f(x)在(a,b)上至少有1个不动点.

证明下证f(x)满足引理1中条件(1).用反证法.若不然，则存在x0∈{a,b}，μ0≥1,使得f(x0)=μ0x0，容易看出μ0>1.考察函数f(t)=(t-1)α-tα(t+1)β+tα,∀t≥1.因f′(t)=α(t-1)α-1-αtα-1(t+1)β+αtα-1-βtα(t+1)β-1<0，故f(t)在[1,∞)上严格单调递减，又当t>1时有f(t)1成立，注意到|x0|≠0，μ0>1,因此有

|f(x0)+x0|α|x0|β=|x0|β|μ0x0-x0|α=(μ0-1)α|x0|α+β<

|f(x0)|α|x0|β.

这与(2)式矛盾，故由引理1可知定理2结论成立.证毕.

在定理2的条件中分别取α=β，α=1，立即得到下面2个推论：

推论1 设f(x)是闭区间[a,b] 上的连续函数，a<01使得(|f(x)-x||x|)α≥(|f(x)||f(x)+x|)α-(|f(x)||x|)α(∀x∈{a,b} )成立，则f(x)在(a,b)上至少有1个不动点.

推论2 设f(x)是闭区间[a,b] 上的连续函数，a<01使得|f(x)-x||x|β≥|f(x)||f(x)+x|β-|f(x)||x|β(∀x∈{a,b})成立，则f(x)在(a,b)上至少有1个不动点.

定理3 设f(x)是闭区间[a,b] 上的连续函数，a<01,β≥0使得

|f(x)+x|α+β≤|f(x)|β|f(x)-x|α+|x|α+β∀x∈{a,b}

(3)

成立，则f(x)在(a,b)上至少有1个不动点.

证明下证f(x)满足引理1中条件(1).用反证法.若不然，则存在x0∈{a,b}，μ0≥1，使得f(x0)=μ0x0，容易看出μ0>1.考察函数f(t)=(t+1)α+β-tβ(t-1)α-1,∀t≥1.因f′(t)=α((t+1)α+β-1-(t-1)α-1tβ)+β((t+1)α+β-1-tβ-1(t-1)α)>0，故f(t)在[1,∞)上严格单调递增，又当t>1时有f(t)>f(1)，即(t+1)α+β>tβ(t-1)α+1对于∀t>1成立,注意到|x0|≠0，μ0>1，因此有

|f(x0)+x0|α+β= |μ0x0+x0|α+β=(μ0+1)α+β|x0|α+β>(μ0β(μ0-1)α+1)|x0|α+β=

|u0x0|β|μ0x0-x0|α+|x0|α+β=

|f(x0)|β|f(x0)-x0|α+|x0|α+β.

这与(3)式矛盾，故由引理1可知定理3结论成立.证毕.

推论3 设f(x)是闭区间[a,b] 上的连续函数，其中a<01使得|f(x)+x|α≤|f(x)-x|α+|x|α(∀x∈{a,b} )成立，则f(x)在(a,b)上至少有1个不动点.

推论4 设f(x)是闭区间[a,b] 上的连续函数，其中a<0

定理4 设f(x)是闭区间[a,b] 上的连续函数，a<0

|f(x)|α|f(x)+x|β≤|f(x)|β|f(x)-x|α∀x∈{a,b}

(4)

成立，则f(x)在(a,b)上至少有1个不动点.

证明下证f(x)满足引理1中的条件(1).用反证法.若不然，则存在x0∈{a,b}，μ0≥1，使得f(x0)=μ0x0，容易看出μ0>1.考察函数f(t)=tα(t+1)β-tβ(t-1)α，∀t>1.因f′(t)=α(tα-1(t+1)β-(t-1)α-1tβ)+β(tα(t+1)β-1-tβ-1(t-1)α)>0，故f(t)在[1,∞)上严格单调递增，又当t>1时有f(t)>f(1)=2β>0，即ta(t+1)β>tβ(t-1)α对∀t>1成立，注意到|x0|≠0，μ0>1，因此有

|f(x0)|β|f(x0)-x0|α.

这与(4)式矛盾，故由引理1可知定理4结论成立.证毕.

在定理4的条件中取α=β=1立即得到下面的推论：

推论6 设f(x)是闭区间[a,b] 上的连续函数，a<0

定理5 设f(x)是闭区间[a,b] 上的连续函数，a<0

|f(x)-x|α|x|α+β≥|f(x)|α|f(x)+x|α+β-|x|2α+β∀x∈{a,b}

(5)

成立，则f(x)在(a,b)上至少有1个不动点.

证明下证f(x)满足引理1中条件(1).用反证法.若不然，则存在x0∈{a,b}，μ0≥1，使得f(x0)=μ0x0，容易看出|x0|≠0，μ0>1.考察函数f(t)=(t-1)α-tα(t+1)α+β+1，∀t≥1.因f′(t)=α((t-1)α-1-tα-1(t+1)α+β-tα(t+1)α+β-1)-β(tα(t+1)α+β-1)<0，故f(t)在[1,∞)上是严格单调递减的，又当t>1时有f(t)1成立，注意到|x0|≠0，μ0>1，因此有

|f(x0)-x0|α|x0|α+β=|x0|α+β|μ0x0-x0|α=(μ0-1)α|x0|2α+β<

-|x0|α+β=|f(x0)|α|f(x0)+x0|α+β-|x0|2α+β.

这与(5)式矛盾，故由引理1可知定理5结论成立.证毕.

在定理5的条件中分别取β=0，α=1与β=0，立即得到下面2个推论：

推论7 设f(x)是闭区间[a,b] 上的连续函数，a<0

推论8 设f(x)是闭区间[a,b] 上的连续函数，a<0

注1 证明Altman型不动点定理所使用的技巧对于研究Banach空间中非线性算子的Altman型不动点存在性问题同样是适用的.

[1] AGARWAL R P,MEEHAN M,O’ REGAN D.Fixed Point Theory and Application[M].Cambridge:Cambridge University Press and Beijing World Publishing Corporation,2001.

[2] AGARWAL R P,O’REGAN D.A.Note on the Existence of Multiple Fixed Point for Multivalued Maps with Applications[J].J. Diff. Eqns.,2000,160:389-403.

[3] SIMON A,VOLKMANN P.Existence of Ground States with Exponential Decay for Semi-Linear Elliptic Equations inRn[J].J. Diff. Eqns.,1988,76:374-390.

[4] 梁展东.Altman定理的一个推广[J].山西大学学报：自然科学版,1986,9(1):1-3.

[5] 贾庆菊.Altman定理的一个注记[J].山西大学学报：自然科学版,1994,17(3):266-268.

[6] 许绍元.Altman定理的推广与改进[J].江西师范大学学报：自然科学版,1995,19(2):149-152.

[7] 许绍元.P1-紧映象的Altman定理的一个推广[J].江西师范大学学报：自然科学版,1996,20(1):89-91.

[8] 许绍元.Banach 空间中压缩映射的新不动点定理[J].赣南师范学院学报,2007,28(6):1-4.

[9] 郭大钧,孙经先.拓扑度的计算及其应用[J].数学研究与评论,1988,8(3):469-480.

[10] 许绍元,谢显华.锥壳中严格集压缩映射的新不动点定理[J].信阳师范学院学报：自然科学版,2011,24(4):440-443.

[11] 陈继乾.P1-紧与半紧1-集压缩映射的Altman定理[J].工程数学学报,1994,11(2):118-122.

[12] 华东师范大学数学系.数学分析[M].北京:高等教育出版社,2010.

(责任编辑 向阳洁)

AltmanTypeFixedPointTheoremsforContinuousFunctions

LI Chuling，XU Shaoyuan

(Department of Mathematics and Statistics,Hanshan Normal University,Chaozhou 521041，Guangdong China)

By means of the properties of continuous functions on closed intervals,a basic fixed point theorem of continuous functions on closed intervals is obtained.By using this basic result,a class of Altman type fixed point theorems of continuous functions is obtained.

continuous functions;fixed point theorem;the existence theorem for roots

1007-2985(2014)05-0006-04

2014-03-25

国家自然科学基金资助项目(10961003)；韩山师范学院理科团队项目(LT201202)

许绍元(1964—)，男，湖北武汉人，韩山师范学院数学与统计学系教授，主要从事非线性泛函分析与分形几何研究；E-mail xushaoyuan@126.com.

O177.91

A

10.3969/j.issn.1007-2985.2014.05.002