关于伪Smarandache函数Z(n)的2个问题*

黄 炜

(宝鸡职业技术学院基础部，陕西 宝鸡 721013)

关于伪Smarandache函数Z(n)的2个问题*

黄 炜

(宝鸡职业技术学院基础部，陕西 宝鸡 721013)

研究了lnZ(n)的均值分布性质，利用初等、解析方法，获得了伪Smarandache函数Z(n)的性质，解决了 Felice Russo提出的2个扩展极限的计算问题.

伪Smarandache函数;分布性质；极限;渐近公式

1 问题的提出

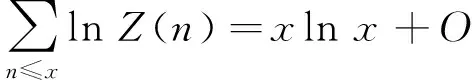
2 引理及其证明

其中C为正的常数，ζ(s)为柯西-黎曼zeta函数.

引理1的证明由参考文献[7]给出.

证明由文献[8]知素数定理可以用几个不同的形式表示，即有

(1)

其中D是可计算的正常数.

由素数定理可表示的几个不同形式的渐近公式(1)，有

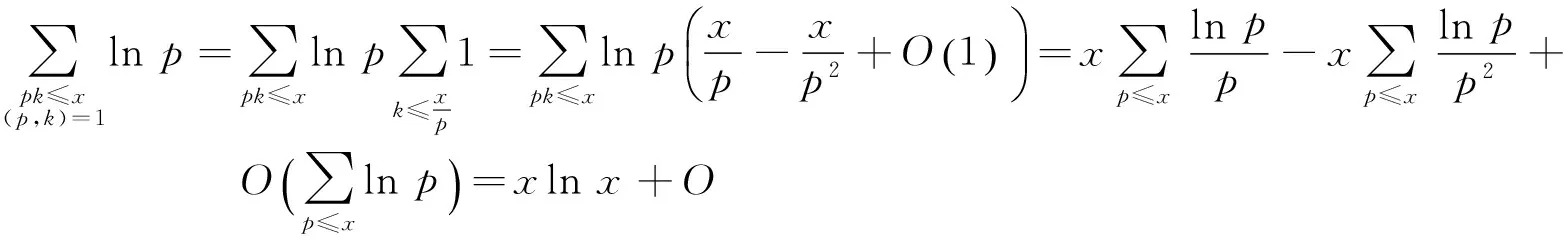
引理2证毕.

引理3 对任意正整数n和k，有:(ⅰ)1≤Z(n)≤2n-1，Z(n)=2n-1当且仅当n=2k其中k为非负整数；(ⅱ)Z(n)=n-1，n=pk，其中p为大于2的素数；(ⅲ)Z(n)≤n-1，其中n不能表达为n=2k的形式.

其证明见参考文献[4-5].

3 定理的证明

xln(2x-1)-x+1+ln 2x=xlnx+O(x).

(2)

接下来估计U(n)的下界.将区间[1,x]中的整数分成如下2个集合A和B：A={m是square-full数，且m∈[1，x]}表示[1，x]；B={m是square-full数，且m∈[1，x]}.于是有

(3)

由集合A的定义及引理1，有

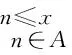
(4)

xlnx+O(x).

(5)

由(3),(4),(5)式，有

(6)

定理1证毕.

定理2，3的证明一方面，由定理 1，有

(7)

另一方面，由Z(n)的定义，有

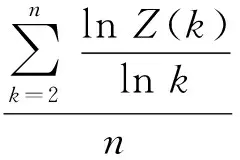
(8)

结合(7)和(8)式，有

(9)

根据定理 1及Z(n)的定义，有

(10)

在定理3中取n→∞时即可推出对应的极限.

[1] FELICE RUSSO.A Set of New Smarandache Function，Sequences and Conjectures in Number Theory[M].USA:American Research Press，2000.

[2] GUNARTO H，MAJUMDAR A.A.K.On Numerical Values ofZ(n)[A].ZHANG Wenpeng.[Eds.],Smaramtache on Number Theory and Smarandache Notions:Proceedings of the Fifth Inter National Conference on Number Theory and Smarandache Notions [C].America:Hexis,2009:74-77.

[3] DAVID GORSKI.The Pseudo Smarandache Function [J].Smarandache Notions Journa,2002,13:140-149.

[4] ALEKSANDAR IVIC.On a Problem of Erdos Involving the Largest Prime Factor of n[J].M. Math.,2005,145:35-46.[5] 马 荣.Smarandache问题研究[M].America:Hexis，2012:449-451.

[6] 黄 炜，刘志峰.关于减法补数复合函数的均值估计[J].西华大学学报：自然科学版,2014,32(1):48-51.

[7] 乐茂华.两个关于伪Smarandache函数的方程[J].吉林化工学院学报,2004,21(4):103-104.

[8] 关文吉,郑亚妮.关于伪Smarandache函数的一个方程[J].纺织高校基础科学学报,2008,21(2):151-153.

[9] TOM M APOSTOL.Introduction to Analytic Number Theory[M].New York:Springer Verlag,1976.

[10] 潘承洞，潘承彪.解析函数论基础[M].北京：科学出版社,1997：98.

(责任编辑 向阳洁)

OnTwoQuestionsofthePseudoSmarandacheFunctionZ(n)

HUANG Wei

(Basic Department，Baoji Vocational Technology College，Baoji 721013,Shaanxi China)

The arithmetical properties of lnZ(n) is studied by the elementary methods and analytic methods,the properties of pseudo Smarandache functionZ(n) are therefore obtained,and thus the two computational problems of limit extension proposed by Felice Russo are solved.

pseudo Smarandache function;distribution properties;limit;asymptotic formula

1007-2985(2014)05-0010-03

2014-02-20

国家自然科学基金资助项目(11071194);陕西省教育厅自然科学基金资助项目(09JK432)

黄 炜(1961—)，男，陕西岐山人，宝鸡职业技术学院基础部教授，硕士，主要从事解析数论与特殊函数研究.

O156.4

A

10.3969/j.issn.1007-2985.2014.05.003