基于极大重叠离散小波变换的金融高频数据波动率估计
秦喜文, 刘文博, 董小刚, 王纯杰, 李纯净
(1.长春工业大学 基础科学学院, 长春 130012; 2.吉林大学 数学学院, 长春 130012;3.吉林建筑大学 基础科学部, 长春 130118)
研究简报
基于极大重叠离散小波变换的金融高频数据波动率估计
秦喜文1,2, 刘文博3, 董小刚1, 王纯杰1, 李纯净1
(1.长春工业大学 基础科学学院, 长春 130012; 2.吉林大学 数学学院, 长春 130012;
3.吉林建筑大学 基础科学部, 长春 130118)
利用极大重叠离散小波变换方法对资产收益的积分波动率进行估计.针对沪深300指数选取不同小波函数估计积分波动率, 计算相对误差统计量.结果表明, 不同小波函数对积分波动率估计不存在显著差异, 但随着抽样频率的增加, 估计精度逐渐提高.对尺度及其相应尺度下的波动率进行对数变换可见, 二者之间存在显著的线性关系, 随着尺度的增加, 波动率逐渐变小.
高频数据; 极大重叠离散小波变换; 波动率估计; 小波方差
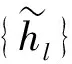
假设X={Xt:t=0,…,N-1}为原始的时间序列数据, 定义运算
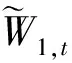
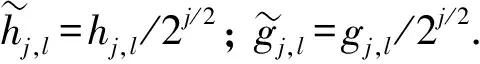
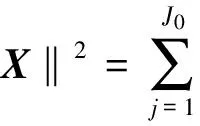
1.2 小波方差 假设{Xt:t=…,-1,0,1,…}表示一个离散参数实值随机过程, 令

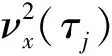
1.3 积分波动率的小波估计 资产收益的积分波动率由下式给出:
其中ωJ,k(dp)表示dp的小波系数.
在给定一组等间隔抽样的时间序列(tj,p(tj))(j=1,2,…,n)下, 构造基于Haar小波的系数:

为了获取积分波动率的小波估计, 将式(6)代入式(5)得
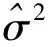
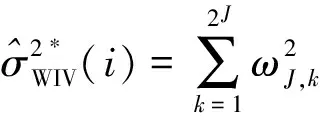
2 实例分析
2.1 利用不同小波函数估计积分波动率 本文所研究的序列为上海和深圳证券交易市场中选取300只A股作为样本编制而成的成份股指数, 即沪深300指数, 选取2010-05—2012-05每间隔5 min的收盘价数据, 共24 192个样本数据.采用股票指数的对数收益率作为分析变量, 令t时刻收盘价为pt, 收益率为rt, 表示为rt=lnpt-lnpt-1.
先分别利用Haar,Daubecheies,Coiflets,Least Asymmetric小波函数对沪深300指数的对数收益率进行极大重叠离散小波变换(MODWT), 得到小波系数, 估计资产收益率的日内积分波动率.同时, 在原始样本数据的基础上进行重采样, 得到间隔为10 min的样本数据, 利用上述方法计算日内积分波动率, 进而计算出不同采样间隔积分波动率相对误差的统计指标, 结果列于表1.
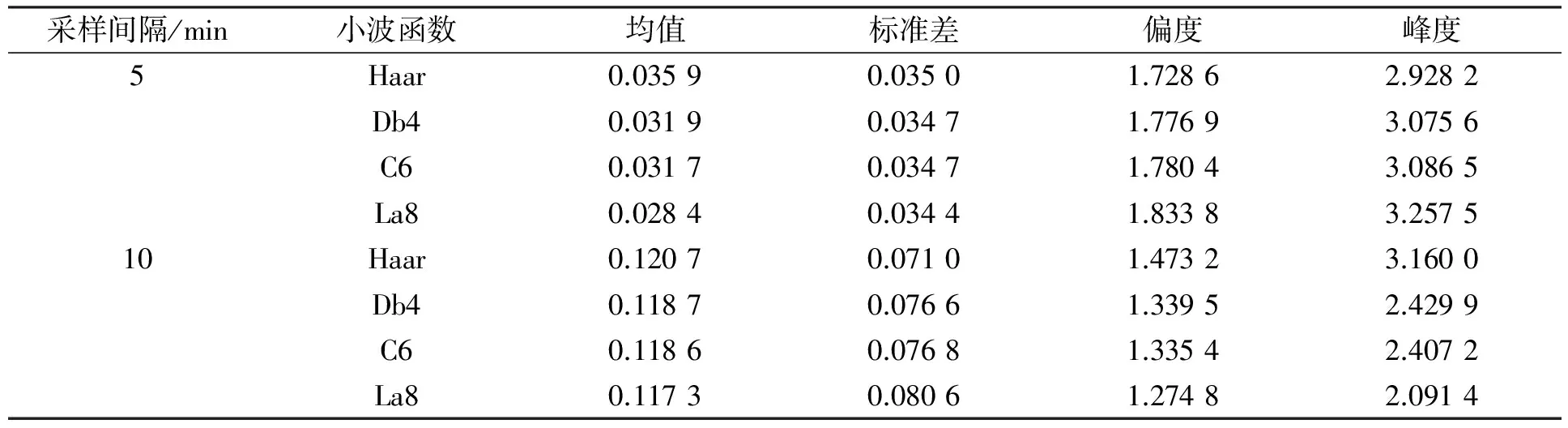
表1 不同小波函数的相对误差统计结果Table 1 Relative errors based on different wavelet functions
由表1可见: 在相同采样间隔情况下, 利用不同小波函数计算积分波动率的均值、标准差、偏度、峰度不存在显著性差异; 5 min采样间隔积分波动率估计的相对误差平均水平和波动性均小于10 min采样间隔, 表明对积分波动率估计时尽量要采用高频数据; 偏度结果表明相对误差均为右偏的, 5 min采样间隔的峰度接近3, 表明近似服从正态分布; 而10 min采样间隔的峰度除Haar小波外均小于3, 表明相对误差分布比正态分布平坦.
图1为小波估计积分波动率相对误差的直方图.由图1可见, 随着抽样频率的降低(采样间隔从5 min到10 min), 无论采用哪种小波函数, 相对误差分布均显著变大, 并且在分布的尾部有更多的极端值出现, 即有更大的误差出现, 高频或超高频数据能产生更多的有效信息, 估计效果更好.对沪深300指数的对数收益率进行极大重叠离散小波变换时, 需要给定使用哪种小波函数, 试验表明, 积分波动率的估计结果对所用的小波并不敏感.
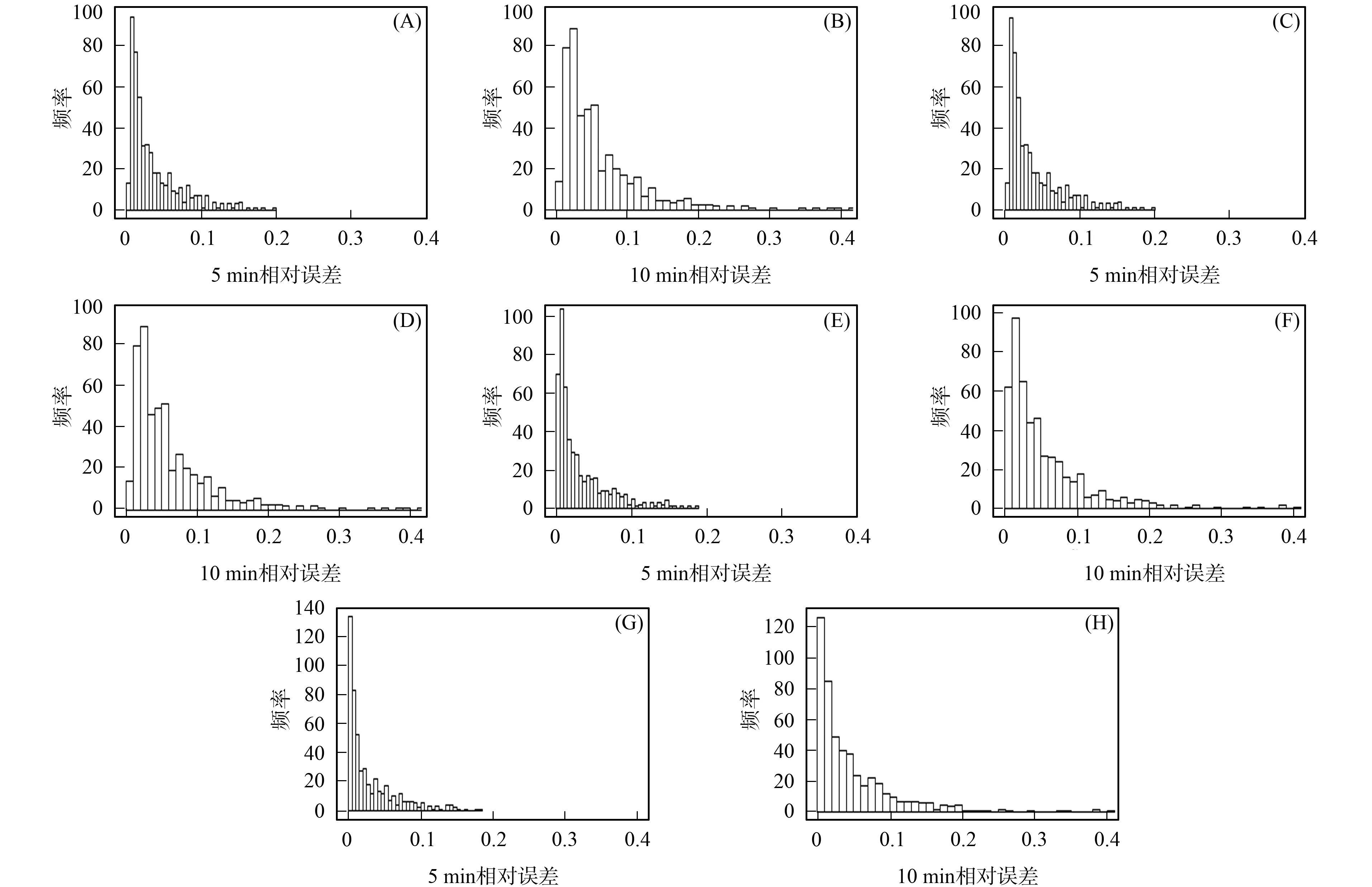
(A),(B) Db4小波估计; (C),(D) Haar小波估计; (E),(F) C6小波估计; (G),(H) La8小波估计.

图2 沪深300指数尺度与波动率的关系Fig.2 Relationship between scale and volatility of Shanghai and Shenzhen 300 indices
2.2 不同尺度与积分波动率的关系 下面考虑基于MODWT方法计算不同尺度τj下的积分波动率估计, 其中尺度τj=2j-1(j=1,2,…,14), 对应的尺度分别为20×5,21×5,22×5,…,213×5 min(约170 d).采用Db小波, 具有n阶消失矩, 而且正则性随n增加而线性增加的小波函数中支集最小的函数.不同尺度积分波动率的结果如图2所示, 其中小尺度对应高频数据, 大尺度对应低频信息.由图2(A)可见, 随着尺度的增加, 积分波动率逐渐变小, 并且近似呈负指数变换.针对尺度和积分波动率分别取自然对数, 由图2(B)可见, 随着尺度的增加, 收益率的积分波动率逐渐变小, 并且二者具有显著的线性关系, 即数据处于高频时, 收益率的积分波动率大, 而在低频时, 积分波动率小.通过离散小波变换系数估计沪深300指数的5 min收益波动率, 从而得到不同尺度下的积分波动率, 对尺度及其相应尺度下的方差进行对数变换可见, 二者之间存在显著的线性关系.
综上所述, 本文利用极大重叠离散小波变换方法对金融高频数据的积分波动率进行了估计, 实证分析表明: 在相同抽样间隔下, 采用不同的小波函数计算积分波动率, 其相对误差的统计指标不存在显著差异性; 在不同抽样间隔下, 随着采样频率的增加(由低频到高频), 积分波动率估计的相对误差逐渐减小, 波动性也逐渐减小, 表明当增加抽样频率时, 能有效提高积分波动率估计的精度; 对尺度及其相应尺度下的方差进行对数变换, 可见二者之间存在显著的线性关系; 随着尺度的增加(频率降低), 积分波动率的估计值逐渐减小.
参考文献
[1]Aït-Sahalia Y, Mykland P A, ZHANG Lan.Ultra High Frequency Volatility Estimation with Dependent Microstructure Noise [J].Journal of Econometrics, 2011, 160(1): 160-175.
[2]FAN Jianqing, WANG Yazhen.Multi-scale Jump and Volatility Analysis for High-Frequency Financial Data [J].Journal of American Statistical Association, 2007, 102(480): 1349-1362.
[3]ZHANG Lan, Mykland P A.Aït-Sahalia Y.A Tale of Two Time Scales: Determining Integrated Volatility with Noisy High-Frequency Data [J].Journal of the American Statistical Association, 2005, 100(472): 1394-1411.
[4]Gallant A R, Hsu C T, Tauchen G.Using Daily Range Data to Calibrate Volatility Diffusions and Extract the Forward Integrated Variance [J].The Review of Economics and Statistics, 1999, 81(4): 617-631.
[5]Voev V, Lunde A.Integrated Covariance Estimation Using High-Frequency Data in the Presence of Noise [J].Journal of Financial Econometrics, 2007, 5(1): 68-104.
[6]FAN Jianqing, LI Yingying, YU Ke.Vast Volatility Matrix Estimation Using High-Frequency Data for Portfolio Selection [J].Journal of the American Statistical Association, 2012, 107(497): 412-428.
[7]Merton R C.On Estimating the Expected Return on the Market: An Exploratory Investigation [J].Journal of Financial Economics, 1980, 8: 323-361.
[8]Lunde A, Hoeg E.Wavelet Estimation of Integrated Volatility [J/OL].2003-08-01.http://econpapers.repec.org/paper/scescecf3/274.htm.
[9]Malliavin P, Mancino M E.Fourier Series Method for Measurement of Multivariate Volatilities [J].Finance and Stochastics, 2002, 6(1): 49-61.
[10]Subbotin A.A Multi-horizon Scale for Volatility [R].Documents de Travail du Centre d’Economie de la Soronne.Paris: Universite Panthéon-Sorbonne (Paris 1), 2008.
[11]Mancino M E, Sanfelici S.Multivariate Volatility Estimation with High Frequency Data Using Fourier Method [M].Handbook of Modeling High-Frequency Data in Finance.New York: Wiley, 2011.
[12]Percival D B, Walden A T.Wavelet Methods for Time Series Analysis [M].Cambridge: Cambridge University Press, 2006.
[13]Daubechies I.Orthonormal Bases of Compactly Supported Wavelets [J].Communications on Pure and Applied Mathematics, 1988, 41(7): 909-996.
[14]Capobianco E.Multiscale Analysis of Stock Index Return Volatility [J].Computational Economics, 2004, 23(3): 219-237.
VolatilityEstimationofFinancialHighFrequencyDataBasedonMaximumOverlapDiscreteWaveletTransform
QIN Xiwen1,2, LIU Wenbo3, DONG Xiaogang1, WANG Chunjie1, LI Chunjing1
(1.SchoolofBasicScience,ChangchunUniversityofTechnology,Changchun130012,China;
2.CollegeofMathematics,JilinUniversity,Changchun130012,China;
3.DepartmentofBasicScience,JilinJianzhuUniversity,Changchun130118,China)
Integrated volatility of asset return was estimated by means of maximum overlap discrete wavelet transform.The different wavelet functions were chosen to estimate the integrated volatility of Shanghai and Shenzhen 300 indices, and relative error statistics was calculated.The results show that integrated volatilities based on different wavelets had no significant difference.The estimated accuracy was improved with the increasing of sampling frequency.There was an obvious linear relationship between logarithmic scale and logarithmic volatility.The volatility decreasd gradually with the scale increasing.
high frequency data; maximum overlap discrete wavelet; volatility estimation; wavelet variance
[8], 下面简要介绍一下积分波动率的小波估计方法.
2014-03-10.
秦喜文(1979—), 男, 汉族, 博士, 副教授, 从事数据分析与统计建模的研究, E-mail: qinxiwen@mail.ccut.edu.cn.通信作者: 董小刚(1961—), 男, 汉族, 博士, 教授, 博士生导师, 从事高频时间序列数据的研究, E-mail: dongxiaogang@mail.ccut.edu.cn.
国家自然科学基金(批准号: 11301036; 11226335; 11071026).
O29
A
1671-5489(2014)06-1222-05
10.13413/j.cnki.jdxblxb.2014.06.23
金融高频数据的波动率估计目前已成为数据分析领域的研究热点[1-2].波动率不仅可以体现金融市场的效率与质量, 而且可作为衡量资产风险的重要指标[3-4].在资产定价、投资组合和风险管理等领域, 准确捕捉收益的波动性, 可正确评判收益水平, 从而有效规避风险[5-6].
针对金融高频数据的波动率非参数估计问题研究目前已有许多结果.如Merton[7]提出了用“已实现波动率”(realized volatility, RV)估计高频数据中波动率的方法.当观测数据是连续的且没有测量误差时, RV是波动率的有效估计.Lunde等[8]首次给出了已实现波动和积分波动率(integrated volatility)的小波估计, 并验证了该估计与Fourier估计[9]效果一样好, 且小波估计比Fourier估计需要更少的样本量, 计算成本更低.Subbotin[10]用小波滤波器, 给出了时变的小波波动率估计, 但其只适合计算固有频率的变差.Mancino等[11]利用高频数据对多元波动率进行了估计.本文引入极大重叠离散小波变换方法估计积分波动率, 用上证综合指数进行实例分析, 并采用不同小波基函数对原始样本进行离散小波变换, 通过得到的小波系数构建波动率的估计, 得出小波函数对波动率估计的影响, 并探求不同尺度下积分波动率的变化规律.
1积分波动率的小波估计方法
赵立芹)

